Hypothesis Tests for Means The context Statistical significance

The context PARAMETERS = population mean (unknown) = population SD (might be known) STATISTICS

Statistical significance We’re trying to decide whether is equal to 0. As usual we

Hypothesis tests are just confidence intervals If we only cared about hypothesis tests for

Hypothesis Test for Cookbook using rejection regions 1. Choose hypotheses – H 0 and

Choose hypotheses Two-sided test: H 0 : = 0 One-sided tests: H 0 :

Define a test statistic Choose or Do you know ? Maybe it comes with

Distribution of the test statistic ASSUME H 0 IS TRUE. Then (if you know

(Standard normal case) The rejection region is a range (or double-range) of values of

Predicting the distribution • If you’re using t, just use t-critical values. • For

Chance of a Type I error Note: IF H 0 is actually true, then

Chance of a Type I error There are two possible bad results: TYPE I

Tradeoff High (say, 10%) then you have a good chance of having a statistically

$Determine p-value The “p-value” is the answer to this question: What fraction of x$

Determine p-value Example: Do a test of H 0: = 0 vs. HA: 0.

Determine p-value Keep it simple? p-value = (for 1 -sided test with z) =

Determine p-value The p-value is the border between ’s for which we reject H

Example: 1969 Draft Lottery Null hypothesis (informally): The numbers for the second half of

Example: 1969 Draft Lottery H 0 : = 183. 5 HA : 183. 5

Hypothesis tests for proportions PARAMETER p = population proportion STATISTICS n = sample size

Hypothesis tests for proportions Test statistic: (Minor subtlety: The distribution of the test statistic

Another example Suppose we have flipped 10000 coins, and obtained 5100 heads. Is this

Another example Our value of p^ is 0. 51. That’s 2. 0 SD’s above

Result of test Is a P-value of 0. 045 good enough to reject H

Slides: 37

Download presentation

Hypothesis Tests for Means The context “Statistical significance” Hypothesis tests and confidence intervals The steps Hypothesis Test statistic Distribution Alpha, and the rejection region Result p-Values One-sided vs. two-sided tests Hypothesis tests for proportions

The context PARAMETERS = population mean (unknown) = population SD (might be known) STATISTICS n = sample size x = sample mean s = sample SD (using n-1) ALSO 0 = conjectured value of

Statistical significance We’re trying to decide whether is equal to 0. As usual we use x as an estimate of . Usually x is at least a little different from 0. But could the difference be due to random variation? IF YES – then we DO NOT REJECT the hypothesis that is really equal to 0. We say that x is not significantly different from 0. IF NO – then we REJECT the hypothesis that = 0. We say that x IS significantly different from 0.

Hypothesis tests are just confidence intervals If we only cared about hypothesis tests for means, we could make this a lot simpler. Just construct a confidence interval for , based on n, x, s (or ) and your favorite confidence level C. If 0 is outside the confidence interval, then we reject the hypothesis that = 0. The significance level is = 1 – C. That’s all there is to it. So why all the complex ritual of a hypothesis test? Because there are other hypothesis tests, for other hypotheses (difference of two means, for example). For those tests, we need the ritual.

Hypothesis Test for Cookbook using rejection regions 1. Choose hypotheses – H 0 and HA. 2. Define a test statistic. 3. Predict the distribution of the test statistic, assuming that H 0 is true. 4. Choose C and . Pick a rejection region. 5. Look at the observed value of the test statistic. Is it in the rejection region? If so, reject H 0.

Choose hypotheses Two-sided test: H 0 : = 0 One-sided tests: H 0 : = 0 or H 0 : = 0 HA : > 0 HA : < 0 Working rule: Always use two-sided tests.

Define a test statistic Choose or Do you know ? Maybe it comes with the null hypothesis. If so, use it.

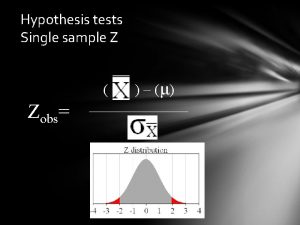
Distribution of the test statistic ASSUME H 0 IS TRUE. Then (if you know ) z has a STANDARD NORMAL distribution. Or (if you’re using s) t has a “t” distribution with n-1 degrees of freedom.

(Standard normal case) The rejection region is a range (or double-range) of values of the test statistic that are (a) UNLIKELY if H 0 is true (b) roughly consistent with the alternative HA. The rejection region should have probability (given H 0). Two-sided case: Rejection region consists of two parts, each with probability /2. - z* /2

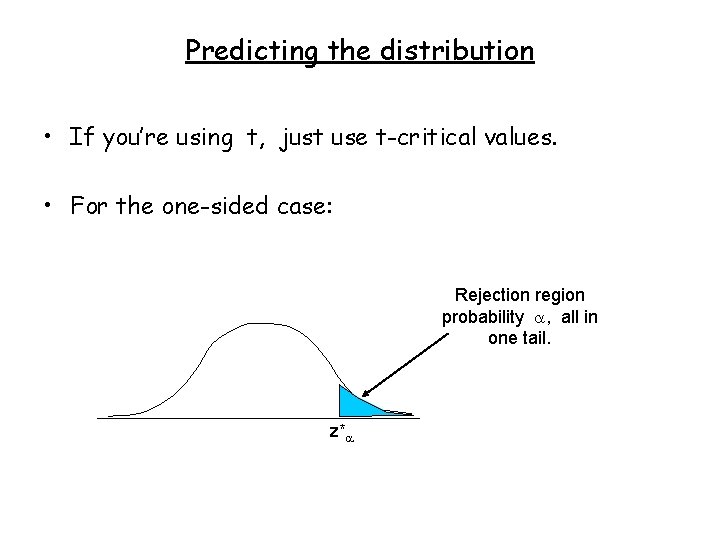
Predicting the distribution • If you’re using t, just use t-critical values. • For the one-sided case: Rejection region probability , all in one tail. z*

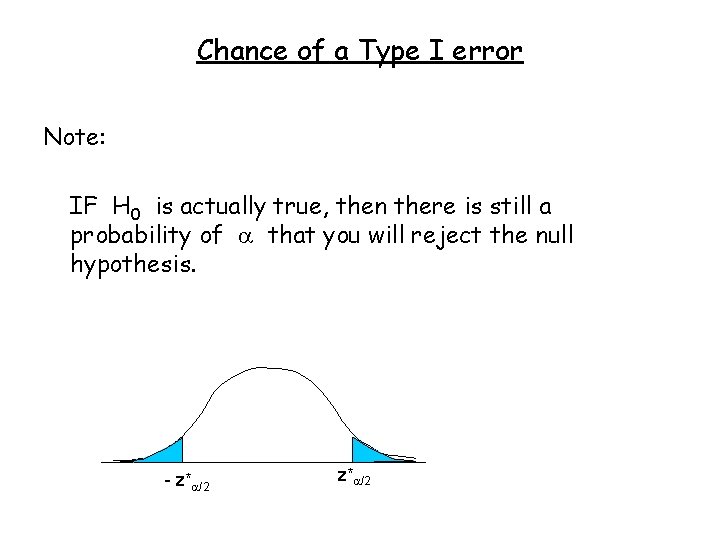
Chance of a Type I error Note: IF H 0 is actually true, then there is still a probability of that you will reject the null hypothesis. - z* /2

Chance of a Type I error There are two possible bad results: TYPE I ERROR (“act of commission”) – reject H 0, when H 0 is actually true. The probability of a Type I error is (given that H 0 is true) TYPE II ERROR (“act of omission”) – don’t reject H 0, when H 0 is actually false. The probability of a Type II error depends on the actual value of

Tradeoff High (say, 10%) then you have a good chance of having a statistically significant result, but it won’t impress anyone. MORE TYPE I ERRORS Low (say, 1%) then your significant results are more convincing, but you’ll have fewer of them. MORE TYPE II ERRORS Is there a way to avoid choosing in advance?

$Determine p-value The “p-value” is the answer to this question: What fraction of x$

Determine p-value The “p-value” is the answer to this question: What fraction of x ‘s are more extreme than the one you actually obtained? If HA: 0 this means, what fraction are further from zero than the value you obtained? If HA: > 0 this means, what fraction are more than the value you obtained? If HA: < 0 this means, what fraction are less than the value you obtained?

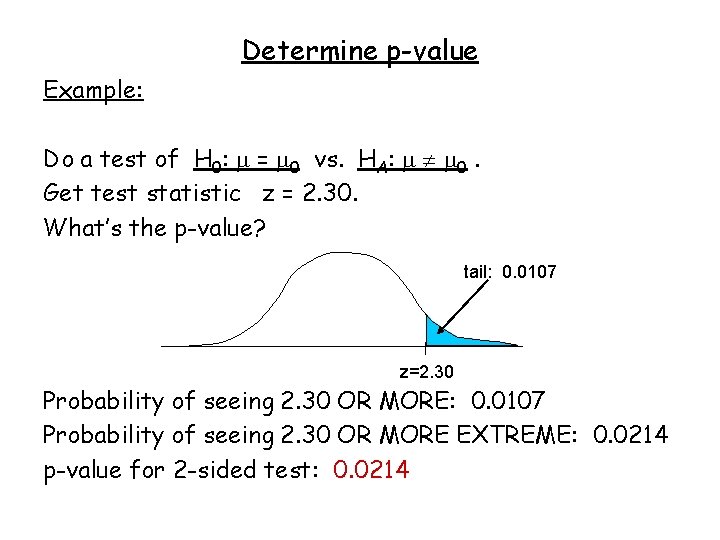
Determine p-value Example: Do a test of H 0: = 0 vs. HA: 0. Get test statistic z = 2. 30. What’s the p-value? tail: 0. 0107 z=2. 30 Probability of seeing 2. 30 OR MORE: 0. 0107 Probability of seeing 2. 30 OR MORE EXTREME: 0. 0214 p-value for 2 -sided test: 0. 0214

Determine p-value Keep it simple? p-value = (for 1 -sided test with z) = 1 - NORMSDIST ( |z| ) (for 2 -sided test with z) = 2 × (1 -NORMSDIST(|z|)) (for 1 -sided test with t) = TDIST ( |t|, n-1, 1 ) (for 2 -sided test with t) = TDIST ( |t|, n-1, 2 ) df number of tails

Determine p-value The p-value is the border between ’s for which we reject H 0 and ’s for which we do not reject H 0. REJECTION REGION VERSION: Pick , and the rejection region, in advance. In this story, the p-value is an afterthought. p-VALUE FIRST VERSION: Find the p-value first. Then if anyone has a favorite , you can… Reject H 0 if p < Do not reject if p > .

Example: 1969 Draft Lottery Null hypothesis (informally): The numbers for the second half of the year were drawn randomly from the population 1, 2, …, 366. (Note: The mean of these numbers is 183. 5, and their standard deviation is 105. 6547. ) Null hypothesis (formally): H 0 : = 183. 5 (and this is one of those cases where = 105. 6547 comes with the null hypothesis) Alternative: HA : 183. 5

Example: 1969 Draft Lottery H 0 : = 183. 5 HA : 183. 5 0 = 183. 5 = 105. 6547 160. 92 Experiment: n = 184, x = _____ Test statistic: = - 2. 898 p-value: 0. 00375 Conclusion: REJECT H 0 (even at 1% significance level)

Hypothesis tests for proportions PARAMETER p = population proportion STATISTICS n = sample size k = number of “hits” p = k / n = sample proportion

Hypothesis tests for proportions Test statistic: (Minor subtlety: The distribution of the test statistic is based on H 0, so we use p 0 in the formula for SE. This is different from what we do in confidence intervals, but not by much. )

Another example Suppose we have flipped 10000 coins, and obtained 5100 heads. Is this result statistically significant?

Another example Suppose we have flipped 10000 coins, and obtained 5100 heads. Is this result statistically significant? Choose: H 0: p = 0. 50 HA: p 0. 50

Another example Suppose we have flipped 10000 coins, and obtained 5100 heads. Is this result statistically significant? Choose: H 0: p = 0. 50 Conditions? OK. HA: p 0. 50

Another example Suppose we have flipped 10000 coins, and obtained 5100 heads. Is this result statistically significant? Choose: H 0: p = 0. 50 HA: p 0. 50 Conditions? OK. Distribution of p^, given H 0: Normal, mean 0. 50, SD=0. 005

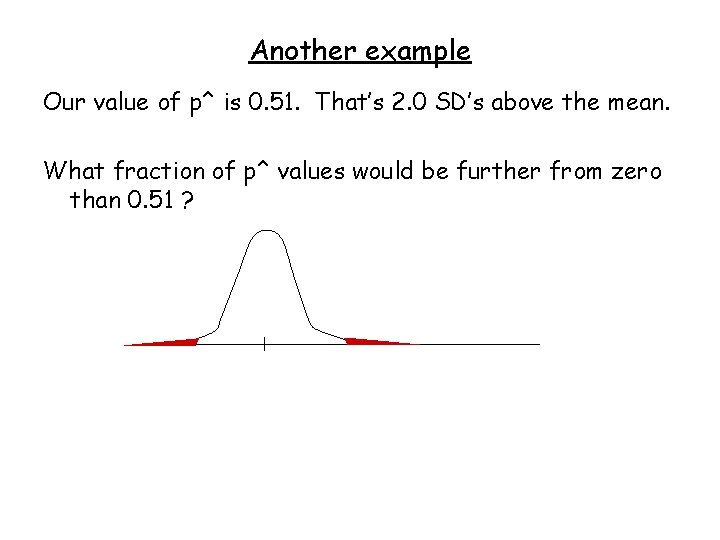
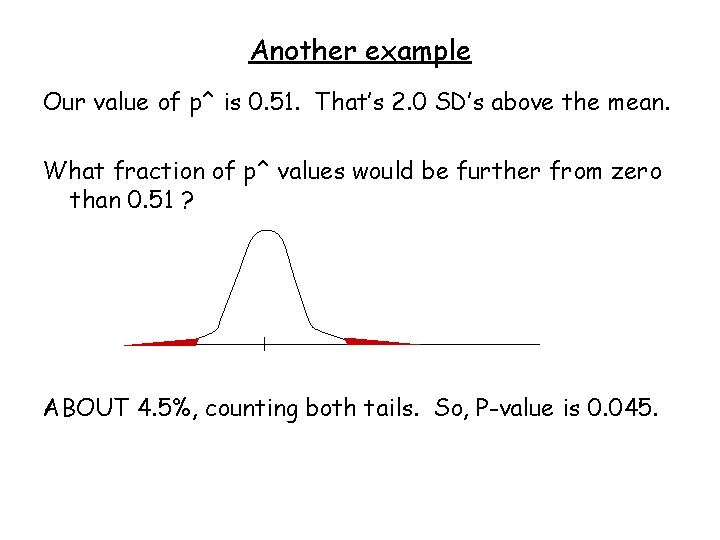
Another example Our value of p^ is 0. 51. That’s 2. 0 SD’s above the mean. What fraction of p^ values would be further from zero than 0. 51 ?

Another example Our value of p^ is 0. 51. That’s 2. 0 SD’s above the mean. What fraction of p^ values would be further from zero than 0. 51 ? ABOUT 4. 5%, counting both tails. So, P-value is 0. 045.

Result of test Is a P-value of 0. 045 good enough to reject H 0?

Result of test Is a P-value of 0. 045 good enough to reject H 0? If we choose = 0. 05, then yes. But that’s a very mild test for such an extraordinary claim.

Result of test Is a P-value of 0. 045 good enough to reject H 0? If we choose = 0. 05, then yes. But that’s a very mild test for such an extraordinary claim. If we pick = 0. 05, then 5% of all our experiments will end in rejecting H 0, even though H 0 is true every time. So we should choose a lower value of . In this case, our result isn’t really “statistically significant. ”