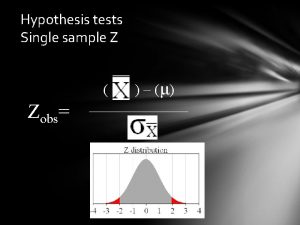
Hypothesis Tests One Sample Means What are hypothesis

Hypothesis Tests One Sample Means

What are hypothesis tests? Calculations that tell us if a value, x, Is it one of the occurs by random chance or not – if sample means that it is statistically aresignificant likely to occur? Is it. . . Statistically significant means that it Is it one occurrence that –isa. NOT random due to a random chance occurrence! isn’t likely to natural variation? occur? – a biased occurrence due to some other reason?

Steps: Notice the steps are the same except we add hypothesis statements – which you will learn today 1) Identify Hypothesis statements, parameters & type of test 2) Conditions 3) Calculations 4) Conclusion, in context

Assumptions for z-test (t-test): YEA – These are the same Have an SRS of context assumptions as confidence intervals!! Sample size < 10% of population • • • Distribution is (approximately) normal – Given – Large sample size – Graph data

Writing Hypothesis statements: • Null hypothesis – is the statement being tested; this is a statement of “no effect” or “no difference” H 0: • Alternative hypothesis – is the statement that we suspect is true Ha:

The form: Null hypothesis H 0: parameter = hypothesized value Alternative hypothesis Ha: parameter > hypothesized value Ha: parameter < hypothesized value Ha: parameter = hypothesized value

P-values • Assuming H 0 is true, the probability that the test statistic would have a value as extreme or more than what is actually observed In other words. . . is it far out in the tails of the distribution?

Statistically significant – • The p-value is as small or smaller than the level of significance (a) • If p > a, “fail to reject” reject the null hypothesis at the a level. • If p < a, “reject” reject the null hypothesis at the a level.

Facts about p-values: • ALWAYS make decision about the null hypothesis! • Large p-values show support for the null hypothesis, but never that it is true! • Small p-values show support that the null is not true. • Double the p-value for two-tail (=) tests • Never accept the null hypothesis!

Calculating p-values • For z-test statistic – – Use normalcdf(lb, ub) – [using standard normal curve] • For t-test statistic – – Use tcdf(lb, ub, df)

Draw & shade a curve & calculate the p-value: 1) right-tail test t = 1. 6; n = 20 P-value =. 0630 2) left-tail test z = -2. 4; n = 15 P-value =. 0082 3) two-tail test t = 2. 3; n = 25 P-value = (. 0152)2 =. 0304

Writing Conclusions: 1) A statement of the decision being made (reject or fail to reject H 0) & why (linkage) AND 2) A statement of the results in context. (state in terms of Ha)

“Since the p-value < (>) a, I reject (fail to reject) the H 0. There is (is not) sufficient evidence to suggest that Ha. ” Be sure to write Ha in context (words)!

Formulas: s known: z= m

Formulas: s unknown: t= m

Example 7: The Fritzi Cheese Company buys milk from several suppliers as the essential raw material for its cheese. Fritzi suspects that some producers are adding water to their milk to increase their profits. Excess water can be detected by determining the freezing point of milk. The freezing temperature of natural milk varies normally, with a mean of -0. 545 degrees and a standard deviation of 0. 008. Added water raises the freezing temperature toward 0 degrees, the freezing point of water (in Celsius). The laboratory manager measures the freezing temperature of five randomly selected lots of milk from one producer with a mean of -0. 538 degrees. Is there sufficient evidence to suggest that this producer is adding water to his milk?

Assumptions: SRS? Normal? • I have an SRS of milk from one producer How do you • The freezing temperature of milk is a normal distribution. know? (given) • s is known Do you know s? What are your hypothesis Ha: m > -0. 545 statements? Is thereofamilk key where m is the true mean freezing temperature word? H 0: m = -0. 545 Plug values into formula. p-value = normalcdf(1. 9566, 1 E 99)=. 0252 Use normalcdf to calculate p-value. a =. 05

Compare your p-value to a & make decision Since p-value < a, I reject the null hypothesis. Conclusion: There is sufficient evidence to suggest that the true mean freezing temperature is greater than -0. 545. This suggests that the producer is adding water to the milk. Write conclusion in context in terms of Ha.

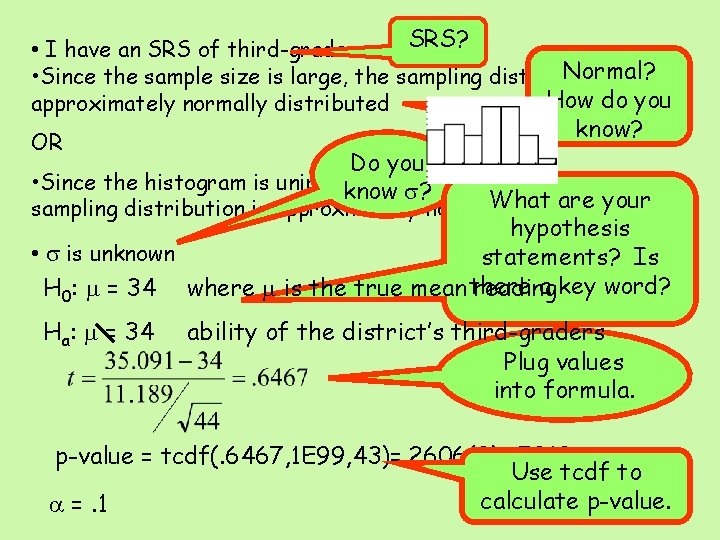
Example 8: The Degree of Reading Power (DRP) is a test of the reading ability of children. Here are DRP scores for a random sample of 44 third-grade students in a suburban district: (data on note page) At the a =. 1, is there sufficient evidence to suggest that this district’s third graders reading ability is different than the national mean of 34?

• I have an SRS of third-graders SRS? Normal? • Since the sample size is large, the sampling distribution is How do you approximately normally distributed OR know? Do you • Since the histogram is unimodal withs? no outliers, the know What are your sampling distribution is approximately normally distributed hypothesis • s is unknown statements? Is a key word? H 0: m = 34 where m is the true mean there reading Ha: m = 34 ability of the district’s third-graders Plug values into formula. p-value = tcdf(. 6467, 1 E 99, 43)=. 2606(2)=. 5212 Use tcdf to calculate p-value. a =. 1

Compare your p-value to a & make decision Since p-value > a, I fail to reject the null hypothesis. Conclusion: There is not sufficient evidence to suggest that the true mean reading ability of the district’s third-graders is different than the national mean of 34. Write conclusion in context in terms of Ha.

Example 9: The Wall Street Journal (January 27, 1994) reported that based on sales in a chain of Midwestern grocery stores, President’s Choice Chocolate Chip Cookies were selling at a mean rate of $1323 per week. Suppose a random sample of 30 weeks in 1995 in the same stores showed that the cookies were selling at the average rate of $1208 with standard deviation of $275. Does this indicate that the sales of the cookies is different from the earlier figure?

Assume: • Have an SRS of weeks • Distribution of sales is approximately normal due to large sample size • s unknown H 0: m = 1323 Ha: m ≠ 1323 where m is the true mean cookie sales per week Since p-value < a of 0. 05, I reject the null hypothesis. There is sufficient to suggest that the sales of cookies are different from the earlier figure.

Example 9: President’s Choice Chocolate Chip Cookies were selling at a mean rate of $1323 per week. Suppose a random sample of 30 weeks in 1995 in the same stores showed that the cookies were selling at the average rate of $1208 with standard deviation of $275. Compute a 95% confidence interval for the mean weekly sales rate. CI = ($1105. 30, $1310. 70) Based on this interval, is the mean weekly sales rate statistically different from the reported $1323?

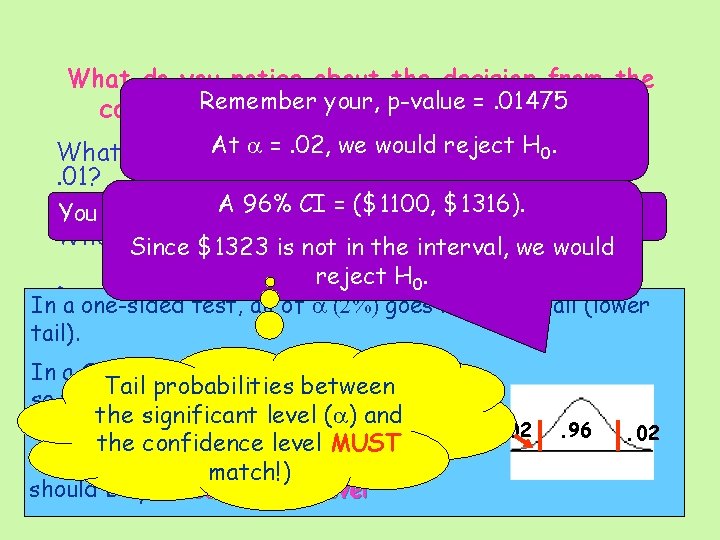
What do you notice about the decision from the Remember p-value =. 01475 confidence intervalyour, & the hypothesis test? a =. 02, would H 0. 10 if a = What decision. Atwould youwe make on reject Example. 01? CI H = ($1100, $1316). You would fail A to 96% reject 0 since the p-value > a. What Since confidence would beinterval, correctwe towould use? $1323 level is not in the reject H 0. that confidence interval provide thetail same In. Does a one-sided test, all of a (2%) goes into that (lower You should use a 99% confidence level for a. Since decision? The 98% CI = ($1084. 40, $1331. 60) tail). two-sided test at =. 01. fail to $1323 is inhypothesis the interval, wea would In If a CI, the tails have equal area – would the hypothesis HTail : m < 1323, what decision probabilitiesreject between H 0. a so test theregive should also be 2% in the at a =. 02? the significant level (a) and CItail = ($1068. 6 , $1346. 40) - Since a$1323 in this. 02 upper =. 02 is. 96 the confidence levelto. MUST Why are we getting different answers? interval we would fail reject H. 0 That leaves 96% in the middle & that Now, what confidence match!) level is appropriate for this alternative should be your hypothesis? confidence level

Matched Pairs Test A special type of t-inference

Matched Pairs – two forms • Pair individuals by certain characteristics • Randomly select treatment for individual A • Individual B is assigned to other treatment • Assignment of B is dependent on assignment of A • Individual persons or items receive both treatments • Order of treatments are randomly assigned or before & after measurements are taken • The two measures are dependent on the individual

Is this an example of matched pairs? 1)A college wants to see if there’s a difference in time it took last year’s class to find a job after graduation and the time it took the class from five years ago to find work after graduation. Researchers take a random sample from both classes and measure the number of days between graduation and first day of employment No, there is no pairing of individuals, you have two independent samples

Is this an example of matched pairs? 2) In a taste test, a researcher asks people in a random sample to taste a certain brand of spring water and rate it. Another random sample of people is asked to taste a different brand of water and rate it. The researcher wants to compare these samples No, there is no pairing of individuals, you have two independent samples – If you would have the same people taste both brands in random order, then it would bean example of matched pairs.

Is this an example of matched pairs? 3) A pharmaceutical company wants to test its new weight-loss drug. Before giving the drug to a random sample, company researchers take a weight measurement on each person. After a month of using the drug, each person’s weight is measured again. Yes, you have two measurements that are dependent on each individual.

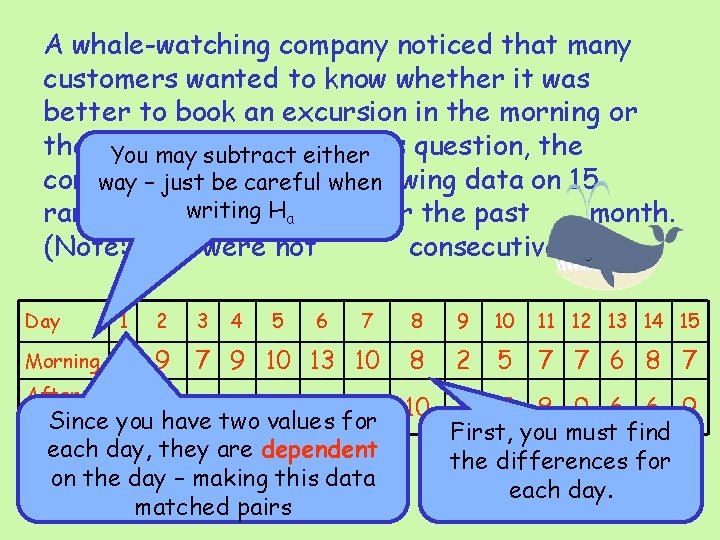
A whale-watching company noticed that many customers wanted to know whether it was better to book an excursion in the morning or the afternoon. To test this question, the You may subtract either company thewhen following data on 15 way – collected just be careful writing Hadays over the past randomly selected month. (Note: days were not consecutive. ) Day 1 8 9 10 11 12 13 14 15 Morning 8 9 7 9 10 13 10 8 2 5 7 7 6 8 7 8 10 9 8 9 11 8 you have two values for each day, they are dependent on the day – making this data matched pairs 10 4 7 8 9 6 6 9 First, you must find the differences for each day. Afternoon Since 2 3 4 5 6 7

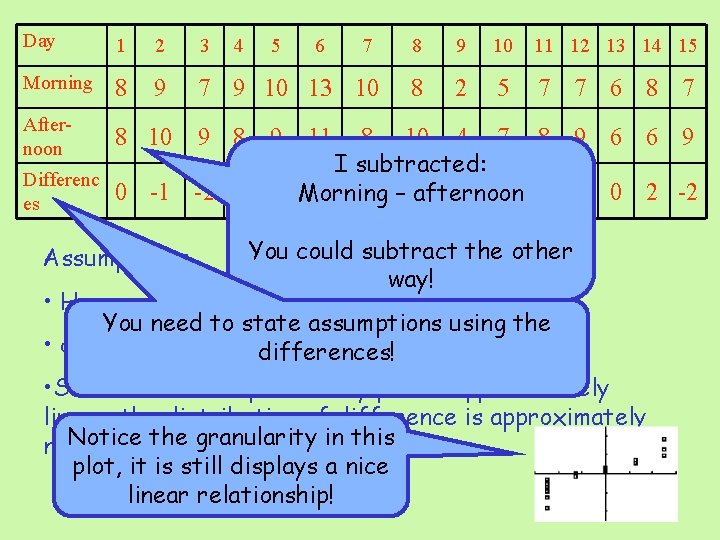
Day 1 2 3 Morning 8 9 7 9 10 13 10 Afternoon 8 10 Differenc es 4 5 9 8 9 6 7 8 9 10 11 12 13 14 15 8 2 5 7 7 6 8 7 11 8 10 4 7 8 9 6 6 9 I subtracted: 0 -1 -2 1 1 Morning 2 2 – -2 -2 -2 -1 -2 0 2 -2 afternoon You could subtract the other way! • Have an SRS of days for whale-watching You need to state assumptions using the • s unknown differences! Assumptions: • Since the normal probability plot is approximately linear, the distribution of difference is approximately Notice the granularity in this normal. plot, it is still displays a nice linear relationship!

Differences 0 -1 -2 1 1 2 2 -2 -1 -2 0 2 Is there sufficient evidence that more whales are sighted in the afternoon? H 0 : m D = 0 Ha : m D < 0 Be careful writing your Ha! Think about how you– If you subtract afternoon subtracted: M-A Hdifferences m. D>0 should Notice morning; we mthen a: more D foris Ifused afternoon & it equals since the nullbeshould the 0 differences + or -? be that there NOat difference. Don’t islook numbers!!!! Where m. D is the true mean difference in whale sightings from morning minus afternoon -2

Differences 0 -1 -2 1 1 2 2 finishing the hypothesis test: -2 -2 -2 -1 -2 0 2 In your calculator, perform t-test Notice athat if the A you using subtracted differences (L 3) -M, then your test statistic t = +. 945, but pvalue would be the same Since p-value > a, I fail to reject H 0. There is insufficient evidence to suggest that more whales are sighted in the afternoon than in the morning. -2