GRAFURI NEORIENTATE recapitulare teorie Profesor Camelia SAVA Colegiul

GRAFURI NEORIENTATE recapitulare teorie Profesor : Camelia SAVA Colegiul Naţional de Informatică “ Traian Lalescu” Hunedoara LOGO

GRAFURI NEORIENTATE - cuprins v definiţie v adiacenţă, incidenţă, gradul unui nod v reprezentarea unui graf prin matricea de adiacenţă, listele de adiacenţă, şirul muchiilor v graf parţial v subgraf v graf complet v lanţ, ciclu v graf conex, componentă conexă v arbori cu rădăcină v arbori binari v parcurgerea arborilor binari C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE Definiţie : Un graf neorientat este o pereche ordonata G=(X, U), unde : - X={x 1, x 2, . . xn } este o mulţime finită şi nevidă. - U este o mulţime finită de perechi neordonate de forma (xi, xj), unde i≠j, şi xi, xj noduri din X. Observaţii: -Elementele mulţimii X se numesc noduri sau vârfuri. Mulţimea X se mai numeşte şi mulţimea nodurilor sau vârfurilor. -Elementele mulţimii U se numesc muchii. Mulţimea U se mai numeşte şi mulţimea muchiilor. Ex: X={1, 2, 3, 4, 5, 6} U={(1, 2), (1, 4), (1, 5), (3, 4), (3, 5), (4, 5)} Muchia (1, 2) este identică cu muchia (2, 1) C. N. I. Traian Lalescu Hunedoara

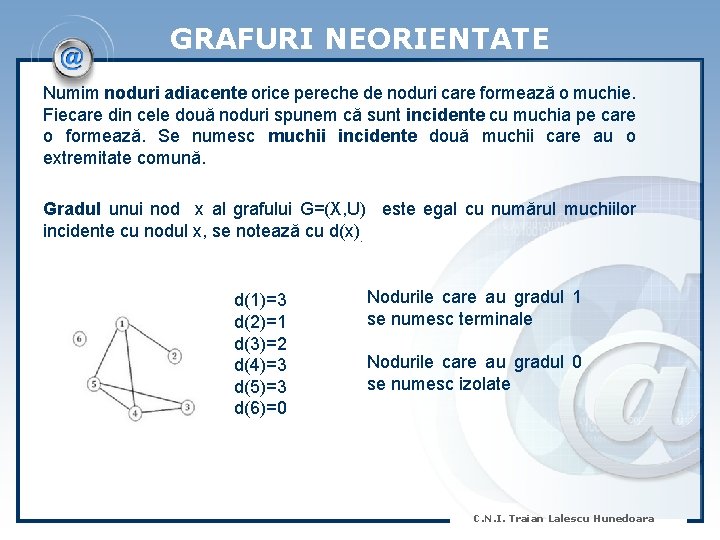
GRAFURI NEORIENTATE Numim noduri adiacente orice pereche de noduri care formează o muchie. Fiecare din cele două noduri spunem că sunt incidente cu muchia pe care o formează. Se numesc muchii incidente două muchii care au o extremitate comună. Gradul unui nod x al grafului G=(X, U) este egal cu numărul muchiilor incidente cu nodul x, se notează cu d(x). d(1)=3 d(2)=1 d(3)=2 d(4)=3 d(5)=3 d(6)=0 Nodurile care au gradul 1 se numesc terminale Nodurile care au gradul 0 se numesc izolate C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE Pentru a reprezenta un graf într-un program, există mai multe modalităţi folosind diverse structuri de date: • reprezentarea unui graf prin matricea de adiacentă; • reprezentarea unui graf prin listele de adiacentă; • reprezentarea unui graf prin şirul muchiilor. Reprezentarea unui graf prin matricea de adiacenţă Fie G=(X, M) un graf neorieritat cu n vârfuri (X={1, 2, . . . , n}) şi m muchii. Matricea de adiacenţă asociată grafului G, este o matrice pătratică de ordinul n, cu elementele definite astfel: altfel spus, ai, j=1, dacă există muchie între i şi j, şi ai, j=0 dacă nu există muchie între i şi j. Matricea de adiacenţă este simetrică faţă de diagonala principală, elementele de pe diagonala principală reţin valoarea 0. C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE Fie graful reprezentat în figura alăturată: Matricea de adiacentă, asociată grafului, este: Obs: gradul unui nod se va calcula ca suma elementelor de pe linia sau coloana corespunzătoare nodului respectiv Reprezentarea unui graf prin listele de adiacenţă Reprezentarea unui graf prin şirul muchiilor Listele de adiacenţă corespunzătoare grafului din figura de mai sus sunt: Se va folosi un vector ce va reţine muchiile grafului: struct muchie {int x, y; }; muchie v[50]; 1 2 3 4 3, 4 1, 2 C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE Definiţie: Fie G=(X, U). Un graf parţial al lui G, este un graf G 1=(X, V), cu V ⊆U. Altfel spus, un graf parţial G 1 este chiar G, sau se obţine din G păstrând toate vârfurile şi suprimând nişte muchii. Exemplu: Pentru graful G=(X, U) de mai jos, construim alăturat graful parţial G 1=(X, V), obţinut prin eliminarea muchiilor ce trec prin vârful 4. G=(X, U) X={1, 2, 3, 4, 5, 6, 7} U ={ u 1, u 2, u 3, u 4, u 5} G 1=(X, V) X={1, 2, 3, 4, 5, 6, 7} V ={ u 1, u 2, u 5} C. N. I. Traian Lalescu Hunedoara

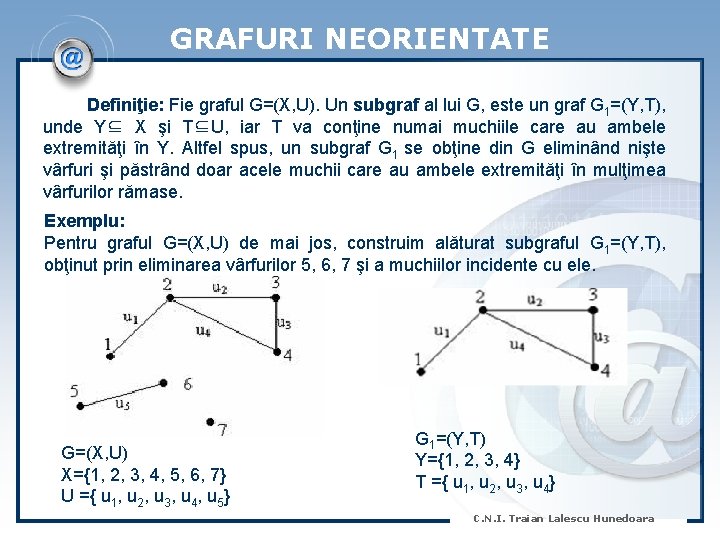
GRAFURI NEORIENTATE Definiţie: Fie graful G=(X, U). Un subgraf al lui G, este un graf G 1=(Y, T), unde Y⊆ X şi T⊆U, iar T va conţine numai muchiile care au ambele extremităţi în Y. Altfel spus, un subgraf G 1 se obţine din G eliminând nişte vârfuri şi păstrând doar acele muchii care au ambele extremităţi în mulţimea vârfurilor rămase. Exemplu: Pentru graful G=(X, U) de mai jos, construim alăturat subgraful G 1=(Y, T), obţinut prin eliminarea vârfurilor 5, 6, 7 şi a muchiilor incidente cu ele. G=(X, U) X={1, 2, 3, 4, 5, 6, 7} U ={ u 1, u 2, u 3, u 4, u 5} G 1=(Y, T) Y={1, 2, 3, 4} T ={ u 1, u 2, u 3, u 4} C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE Definiţie: Fie un graf neorientat G=(X, U). Graful G se numeşte complet dacă oricare două noduri distincte sunt adiacente. Un graf neorientat complet cu n noduri se notează Kn. Ex: K 5 Observaţii: - un graf complet cu n noduri are exact n*(n-1)/2 muchii - gradul fiecărui nod într-un un graf complet cu n noduri este egal cu n-1 C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE Fie un graf G=(X, U) cu vârfurile X={x 1, x 2, …, xn}. Definiţie: Se numeşte lanţ în graful G =(X, U) succesiunea de vârfuri L=[ xi 1, xi 2, …, xik] cu proprietatea că două vârfuri consecutive din L sunt adiacente, adică muchiile [ xi 1, xi 2], [xi 2, xi 3] …[xik-1, xik] sunt din U. Un lanţ este elementar dacă toate vârfurile sale sunt distincte. Altfel este neelementar. Exemplu: - lanţ elementar: 5 -9 -7 -6 -10 - lanţ neelementar: 5 -9 -7 -6 -7 -2 -6 -7 Numărul de muchii al unui lanţ reprezintă lungimea lanţului. C. N. I. Traian Lalescu Hunedoara

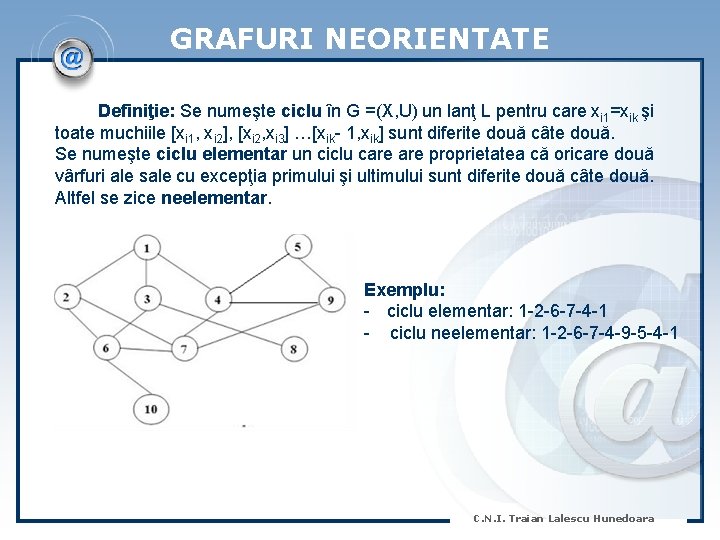
GRAFURI NEORIENTATE Definiţie: Se numeşte ciclu în G =(X, U) un lanţ L pentru care xi 1=xik şi toate muchiile [xi 1, xi 2], [xi 2, xi 3] …[xik- 1, xik] sunt diferite două câte două. Se numeşte ciclu elementar un ciclu care proprietatea că oricare două vârfuri ale sale cu excepţia primului şi ultimului sunt diferite două câte două. Altfel se zice neelementar. Exemplu: - ciclu elementar: 1 -2 -6 -7 -4 -1 - ciclu neelementar: 1 -2 -6 -7 -4 -9 -5 -4 -1 C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE Definiţie: Un graf orientat G=(X, U) se numeşte conex dacă pentru oricare două vârfuri distincte x, y �X există un lanţ cu extremităţile x şi y. Exemplu: Definiţie: Se numeşte componentă conexă a unui graf neorientat G=(X, U) un subgraf conex al său maximal în raport cu această proprietate (oricare ar fi un vârf din subgraf, nu există un lanţ între acel vârf şi vârfurile care nu fac parte din subgraf). Exemplu: componenta conexă 1: componenta conexă 2: componenta conexă 3: 1, 2, 4, 5 3, 7 6 C. N. I. Traian Lalescu Hunedoara

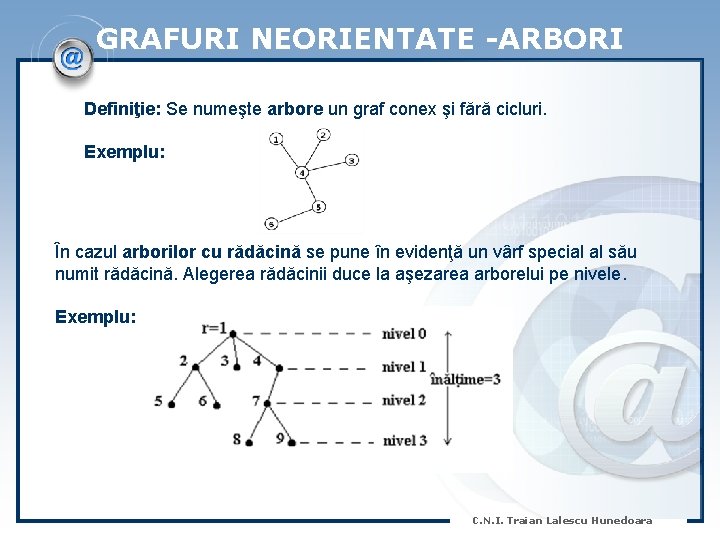
GRAFURI NEORIENTATE -ARBORI Definiţie: Se numeşte arbore un graf conex şi fără cicluri. Exemplu: În cazul arborilor cu rădăcină se pune în evidenţă un vârf special al său numit rădăcină. Alegerea rădăcinii duce la aşezarea arborelui pe nivele. Exemplu: C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE -ARBORI Tatăl unui nod este nodul adiacent cu acesta de pe nivelul anterior numit si ascendent direct. Fiul unui nod este nodul adiacent cu cel curent aflat pe nivelul următor. Două noduri care au acelaşi tată se numesc fraţi. Nodurile care nu au fii se numesc noduri terminale sau frunze. OBSERVATIE: Un nod poate avea un singur tată dar 0 sau mai mulţi fii. Structura unui arbore admite o definiţie recursivă adică orice fiu al unui nod din arbore este la rândul său arbore (subarbore). Reprezentarea arborilor se face folosind vectorul de taţi cu semnificaţia : t[i]=tatăl vârfului i Observaţii: 1) Rădăcina este singurul nod care nu are tată : t[r]=0; 2) Nodurile care sunt fraţi au acelaşi tată deci au aceeaşi valoare în t[i]; 3) Numărul de fii ai unui nod este egal cu numărul de apariţii al nodului în t; 4) Frunzele sunt nodurile care nu apar in vectorul de taţi; 5) Un lanţ care pleacă dintr-un nod dat se poate identifica folosind vectorul de taţi; C. N. I. Traian Lalescu Hunedoara

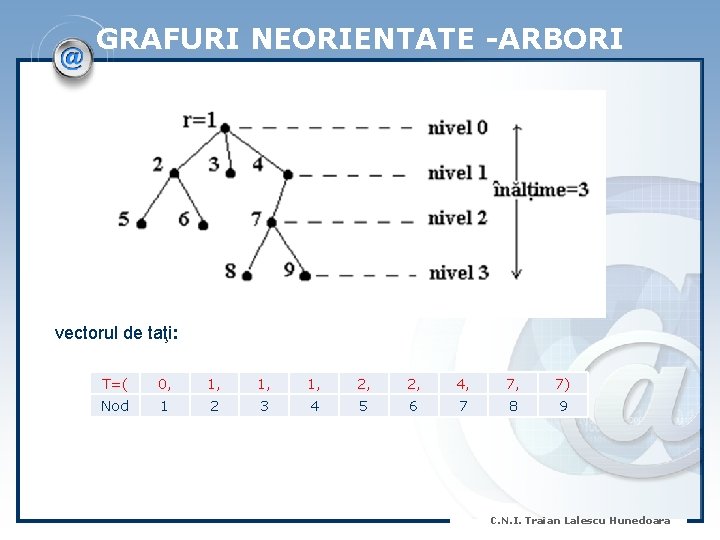
GRAFURI NEORIENTATE -ARBORI vectorul de taţi: T=( 0, 1, 1, 2, 4, 7) Nod 1 2 3 4 5 6 7 8 9 C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE -ARBORI Definiţie: Un arbore binar este o mulţime finită de noduri care este fie vidă, fie reprezintă un arbore ordonat în care fiecare nod are cel mult doi descendenţi. Un arbore binar conţine cel mult doi subarbori, pe care îi numim subarbore stâng, respectiv subarbore drept. Exemplu: Definiţie: Arborele binar complet este arborele care exact doi fii pentru fiecare nod. Exemplu: C. N. I. Traian Lalescu Hunedoara

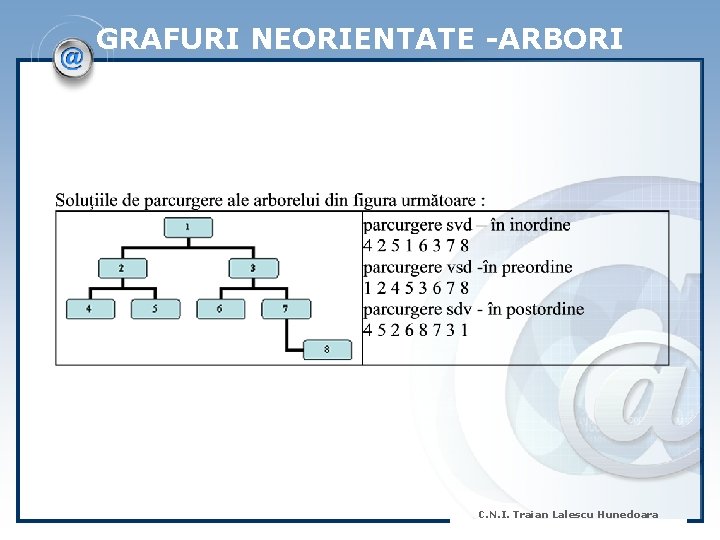
GRAFURI NEORIENTATE -ARBORI Parcurgerea arborilor binari Prin parcurgere se înţelege vizitarea fiecărui nod al arborelui. Principalele modalităţi de parcurgere ale unui arbore binar sunt: A) Arborii binari pot fi parcurşi prin metode specifice grafurilor: în adâncime, în lăţime B) Metode specifice arborilor binari : - Parcurgerea în inordine (stânga –vârf – dreapta SVD) – se parcurge mai întâi subarborele stâng, apoi vârful, apoi subarborele drept. - Parcurgerea în preordine (vârf- stânga – dreapta VSD) – se parcurge mai întâi vârful, apoi subarborele stâng, apoi subarborele drept. - Parcurgerea în postordine (stânga – dreapta – vârf SDV) – se parcurge mai întâi subarborele stâng, apoi subarborele drept şi la sfârşit vârful. C. N. I. Traian Lalescu Hunedoara

GRAFURI NEORIENTATE -ARBORI C. N. I. Traian Lalescu Hunedoara

viitori programatori ! LOGO