Geometria Euclidiana revisitada A reta de Euler Leonhard

Geometria Euclidiana revisitada A reta de Euler Leonhard Euler (1707 -1783) João Lucas Marques Barbosa Universidade Federal do Ceará lucas@sbm. org. br

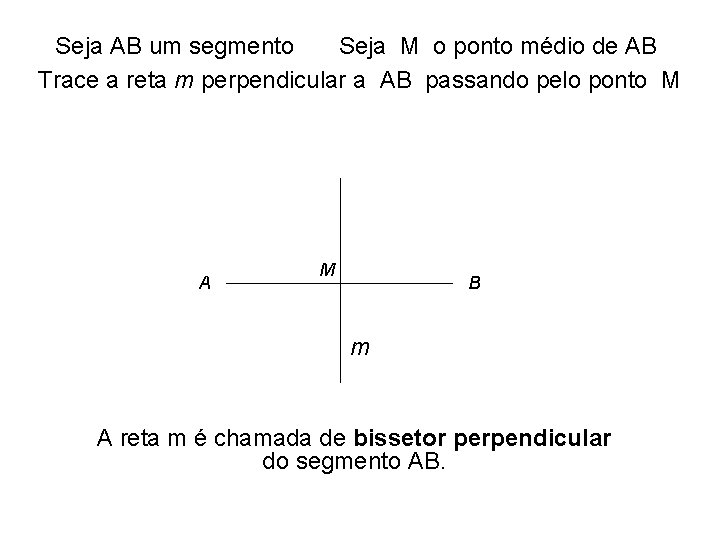
Seja AB um segmento Seja M o ponto médio de AB Trace a reta m perpendicular a AB passando pelo ponto M A M B m . . A reta m é chamada de bissetor perpendicular do segmento AB.

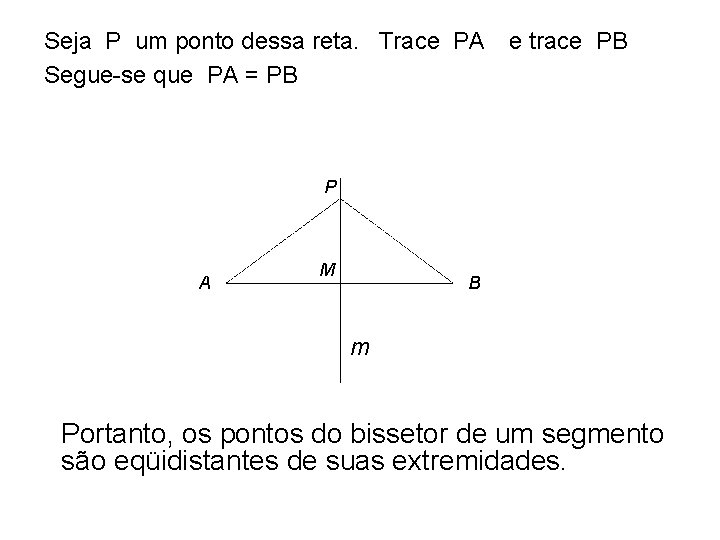
Seja P um ponto dessa reta. Trace PA e trace PB Segue-se que PA = PB P A M B m Portanto, os pontos do bissetor de um segmento são eqüidistantes de suas extremidades. . .

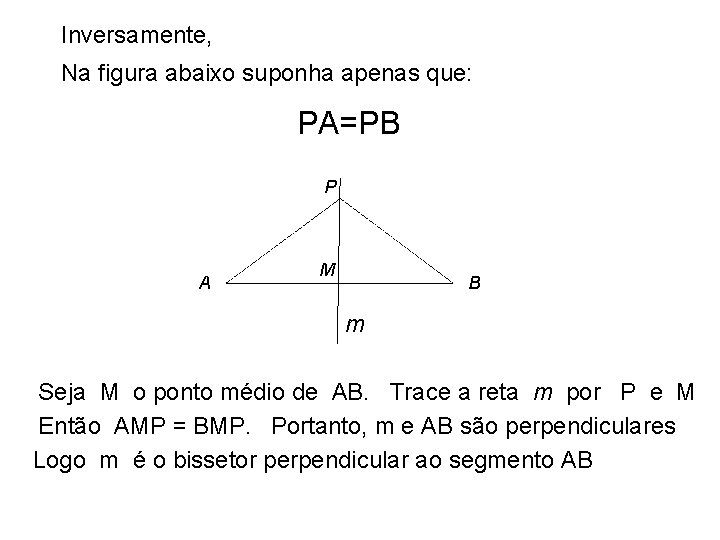
Inversamente, Na figura abaixo suponha apenas que: PA=PB P A M B m Seja M o ponto médio de AB. Trace a reta m por P e M Então AMP = BMP. Portanto, m e AB são perpendiculares Logo. . m é o bissetor perpendicular ao segmento AB

Provamos portanto o seguinte teorema: Teorema: O bissetor perpendicular ao segmento AB é constituído dos pontos eqüidistantes de A e de B.

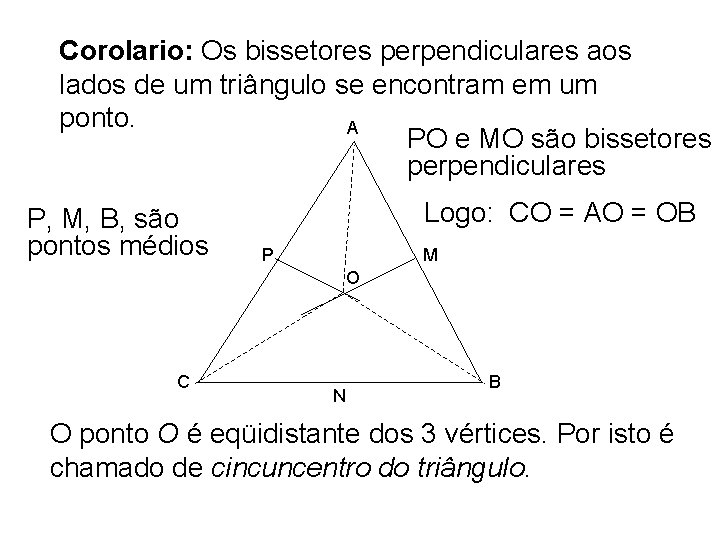
Corolario: Os bissetores perpendiculares aos lados de um triângulo se encontram em um ponto. A PO e MO são bissetores perpendiculares P, M, B, são pontos médios Logo: CO = AO = OB P M O C N B O ponto O é eqüidistante dos 3 vértices. Por isto é chamado de cincuncentro do triângulo. . .

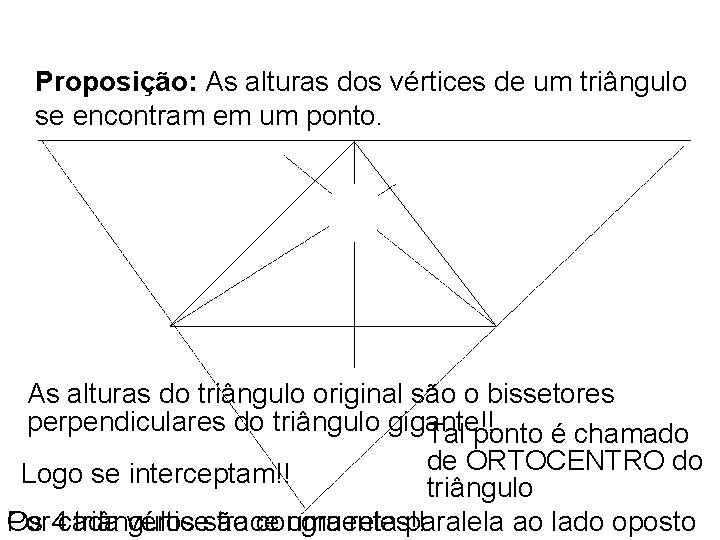
Proposição: As alturas dos vértices de um triângulo se encontram em um ponto. As alturas do triângulo original são o bissetores perpendiculares do triângulo gigante!! Tal ponto é chamado de ORTOCENTRO do Logo se interceptam!! Trace as 3 alturas do triângulo Por 4 cada Os triângulos vérticesão trace congruentes!! uma reta paralela ao lado oposto

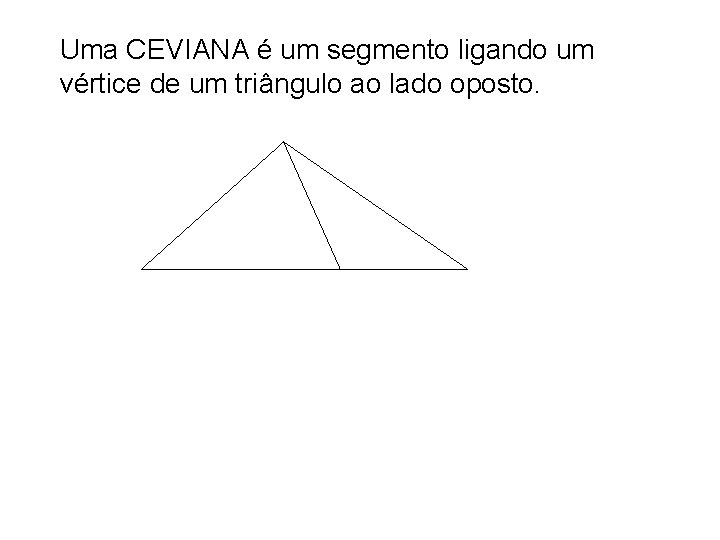
Uma CEVIANA é um segmento ligando um vértice de um triângulo ao lado oposto.

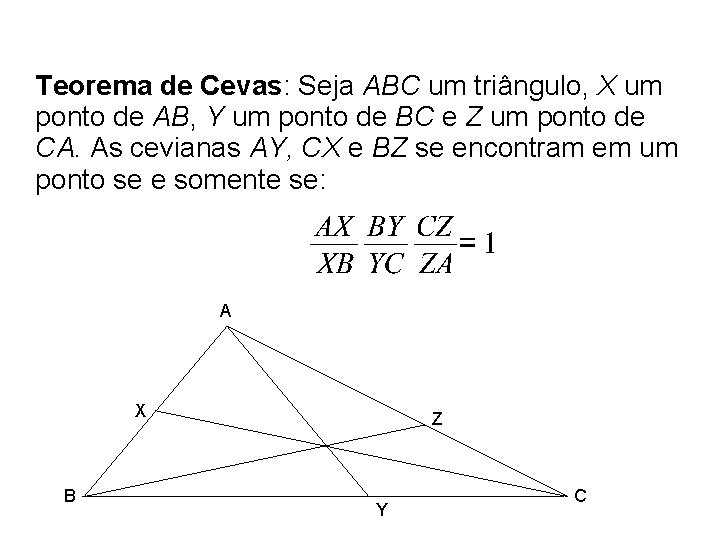
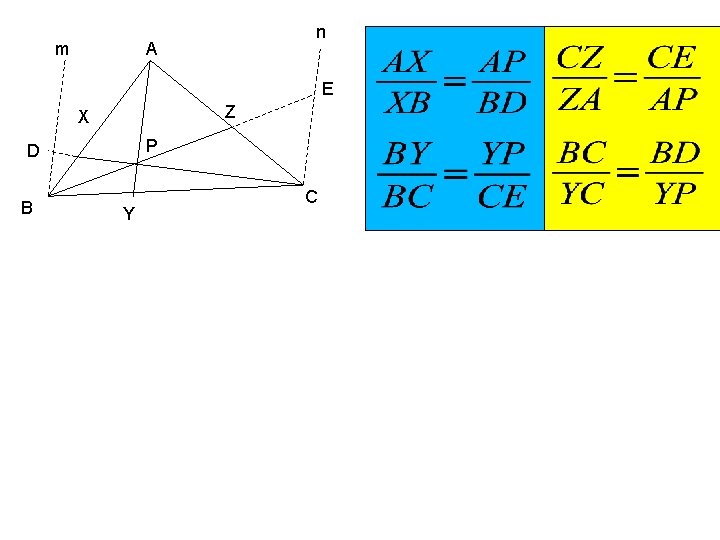
Teorema de Cevas: Seja ABC um triângulo, X um ponto de AB, Y um ponto de BC e Z um ponto de CA. As cevianas AY, CX e BZ se encontram em um ponto se e somente se: A X B Z Y C

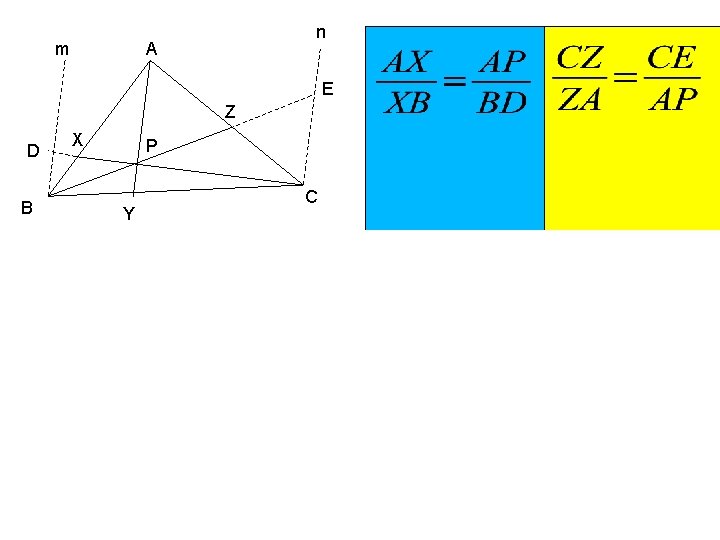
m n A E Z X D P B C Y A Trace retas m e n paralelas a AY Prolongue CX até D em m Prolongue BZ até E em n A E Z D B X P P C

m n A E Z X P D B C Y E P B Y D C B P Y C

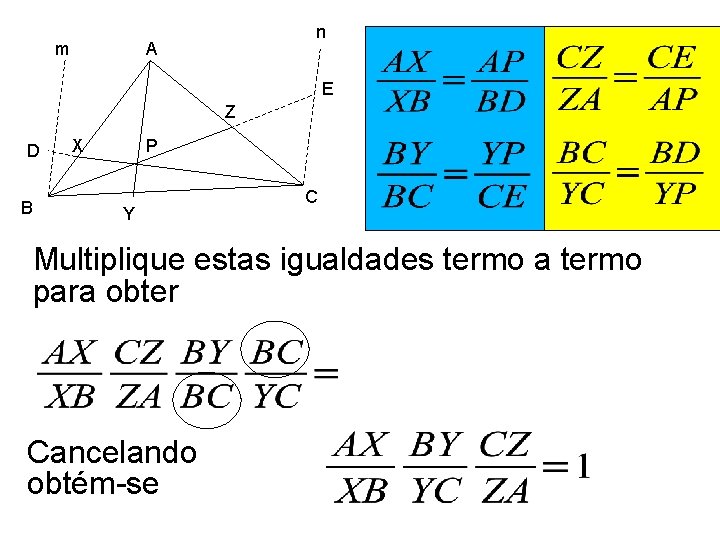
m n A E Z D B X P Y C Multiplique estas igualdades termo a termo para obter Cancelando obtém-se

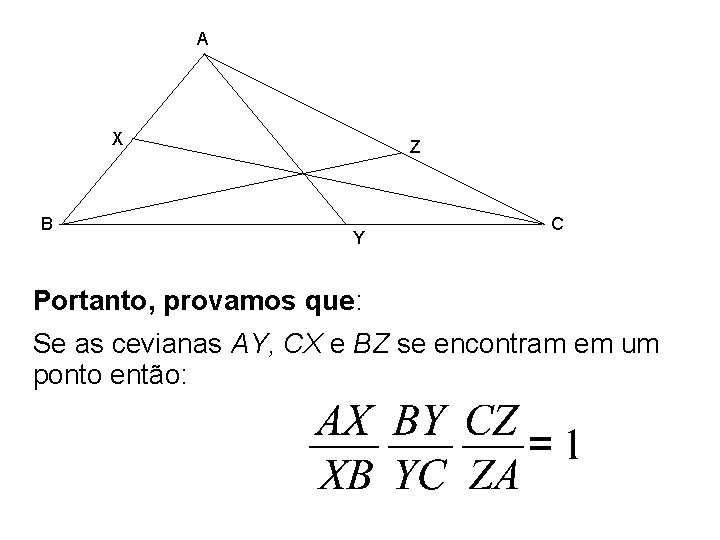
A X B Z Y C Portanto, provamos que: Se as cevianas AY, CX e BZ se encontram em um ponto então:

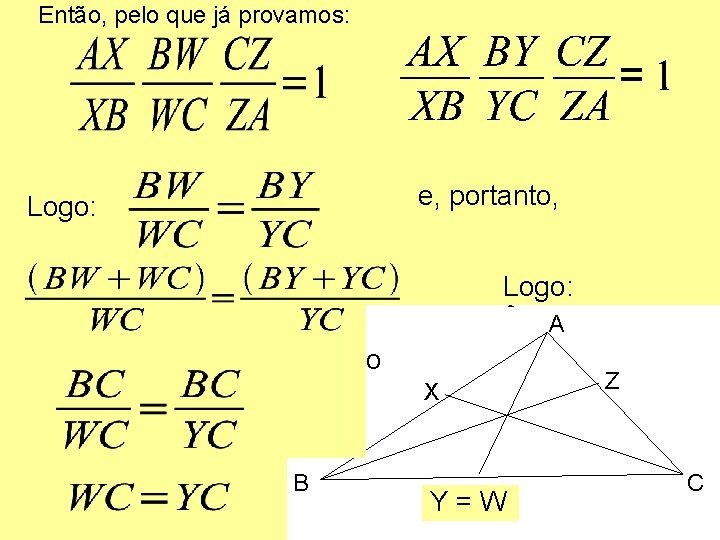
Então, pelo que já provamos: Vamos agora provar que: Dado um triângulo ABC em que AY, BZ e CX são cevianas, se e, portanto, Logo: então as cevianas se encontram em um. Logo: ponto. A PROVA: Escolha um ponto W em BC de modo que AW, BZ e CX se encontrem. B X Y =W W Z C

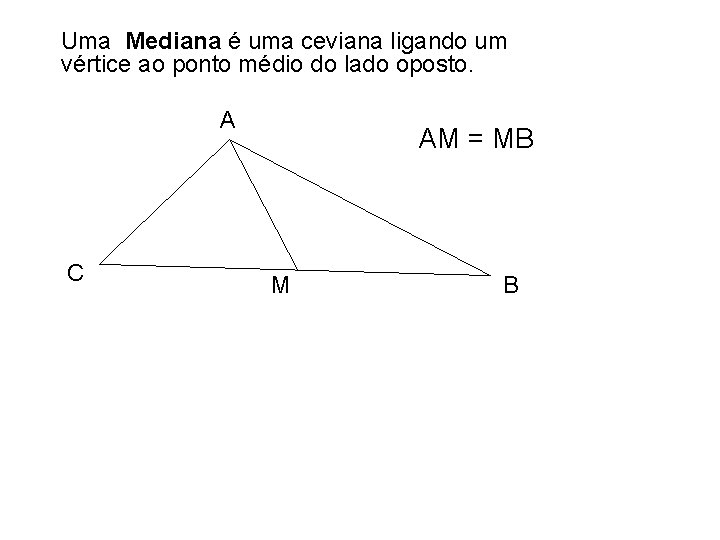
Uma Mediana é uma ceviana ligando um vértice ao ponto médio do lado oposto. A C AM = MB M B

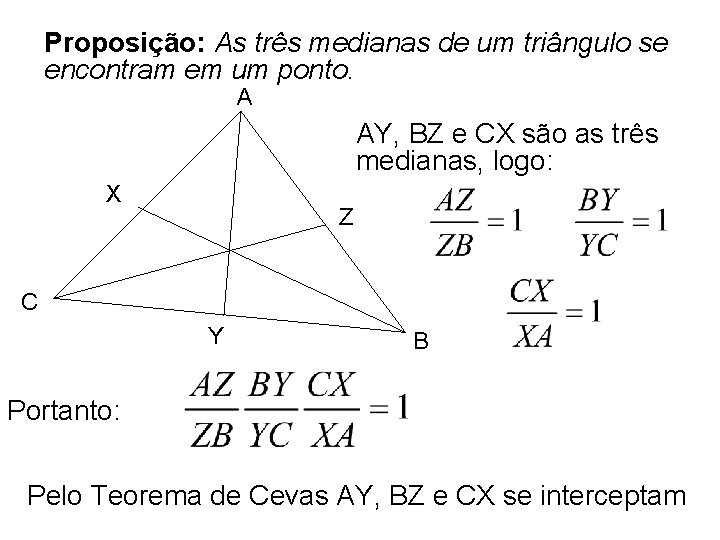
Proposição: As três medianas de um triângulo se encontram em um ponto. A AY, BZ e CX são as três medianas, logo: X Z C Y B Portanto: Pelo Teorema de Cevas AY, BZ e CX se interceptam

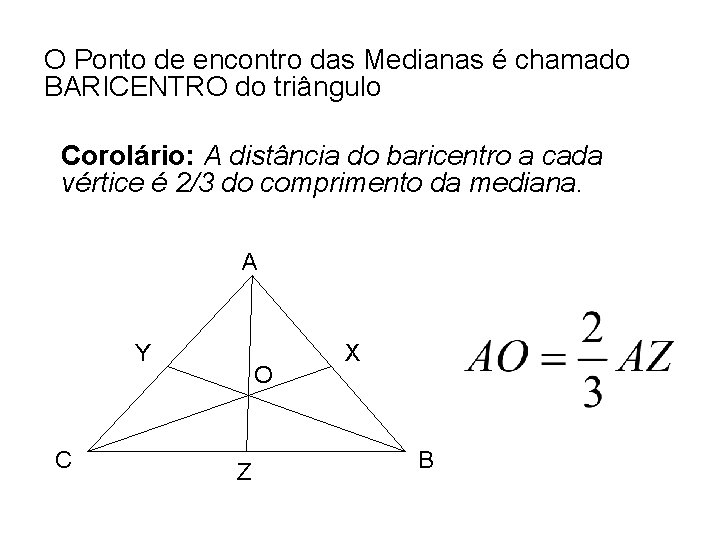
O Ponto de encontro das Medianas é chamado BARICENTRO do triângulo Corolário: A distância do baricentro a cada vértice é 2/3 do comprimento da mediana. A Y C O Z X B

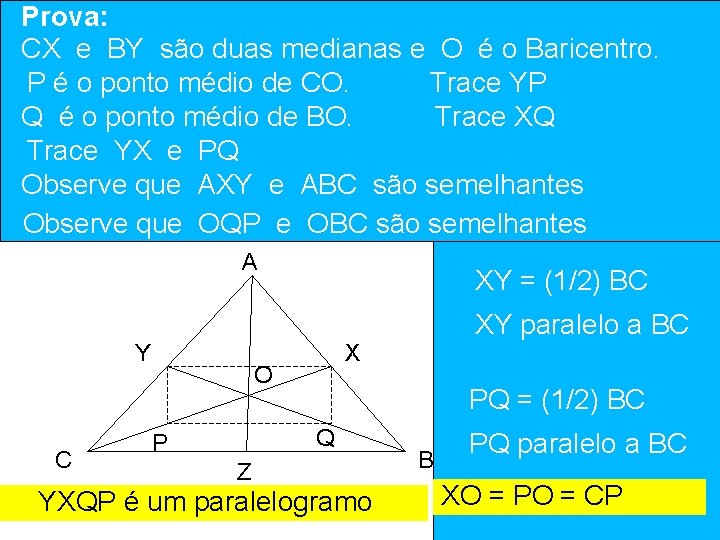
Prova: CX e BY de sãoencontro duas medianas e O ééochamado Baricentro. O Ponto das Medianas PBARICENTRO é o ponto médio CO. Trace YP dode triângulo Q é o ponto médio de BO. Trace XQ Trace YX e PQ Corolário: A distância do baricentro a cada vérticeque é 2/3 do comprimento da mediana. Observe AXY e ABC são semelhantes Observe que OQP e OBC são semelhantes A Y C XY = (1/2) BC X O PQ = (1/2) BC Q P XY paralelo a BC Z YXQP é um paralelogramo B PQ paralelo a BC XO = PO = CP

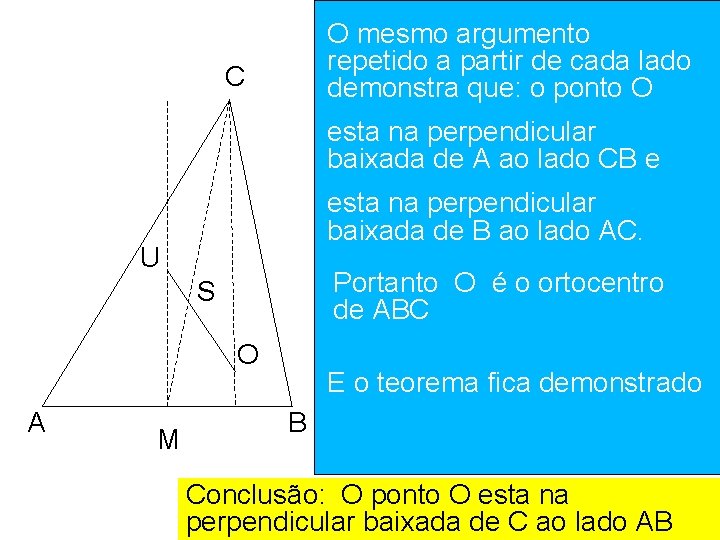
Teorema: Dado um triângulo ABC, seja U o circuncentro, S o baricentro e O o ortocentro. Então os pontos U, S e O estão sobre uma mesma reta (a qual é denominada reta de Euler). Alem disto, eles estão situados na reta na ordem U, S, O e estão espaçados de modo que SO = 2 SU.

O mesmo argumento M = ponto médio de AB repetido a partir de cada lado demonstra que: o ponto O U = circuncentro de ABC C estaé na perpendicular MU perpendicular a AB baixada de A ao lado CB e S = Baricentro de ABC esta na perpendicular baixada de. US B ao AC. O Prolongue atélado o ponto de modo que SO = 2 SU Portanto O é o ortocentro Lembre de ABCque SC = 2 SM U S O A M Portanto: SUM e SOC semelhantes Esão o teorema fica demonstrado B Logo: MU e CO são paralelos Conclusão: O ponto O esta na perpendicular baixada de C ao lado AB

Terminamos!! Muito Obrigado

João Lucas Barbosa lucas@mat. ufc. br