Section 7 1 Introduction to Graph Theory Euler

Section 7. 1 Introduction to Graph Theory

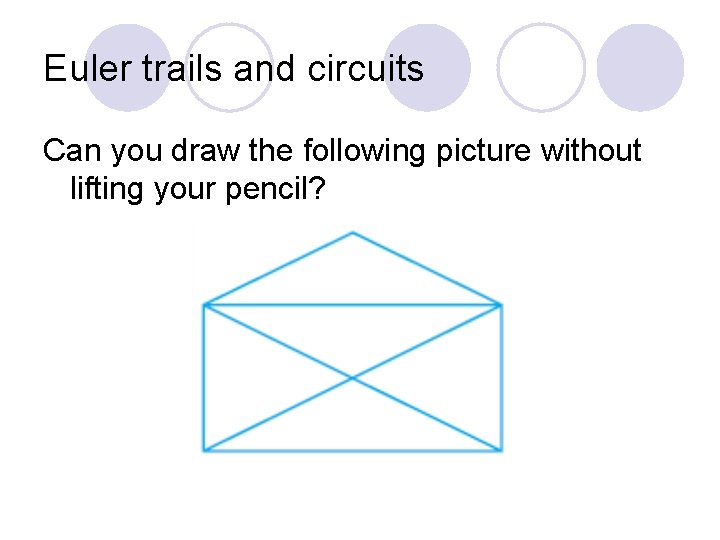
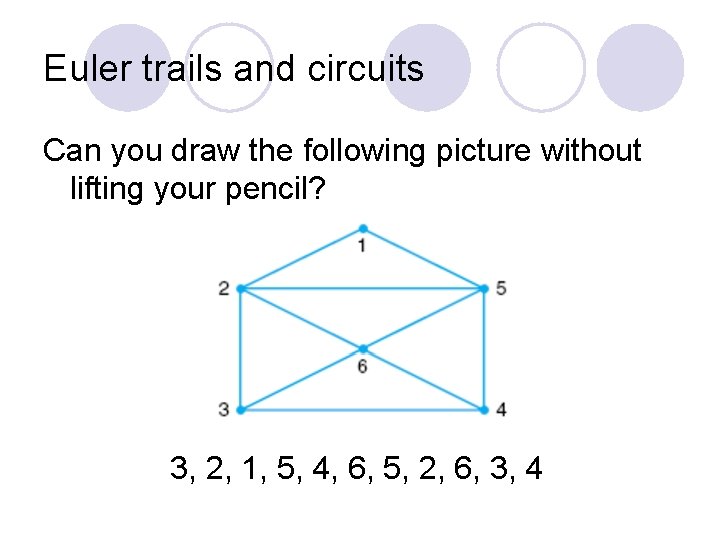
Euler trails and circuits Can you draw the following picture without lifting your pencil?

Euler trails and circuits Can you draw the following picture without lifting your pencil?

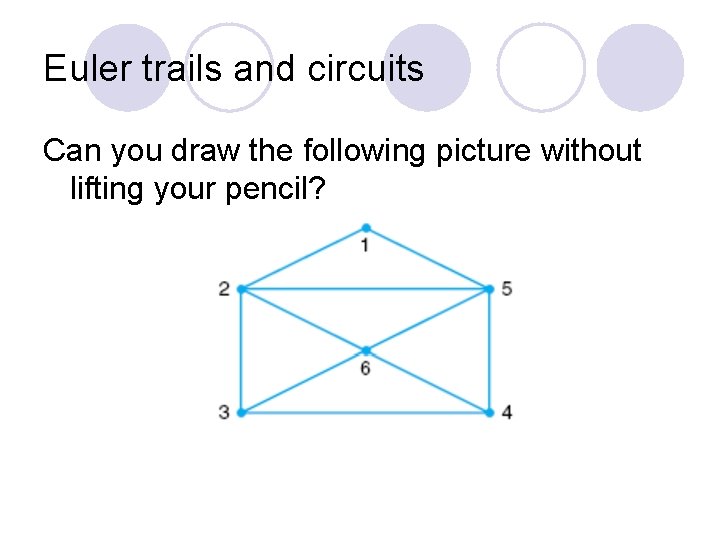
Euler trails and circuits Can you draw the following picture without lifting your pencil? 3, 2, 1, 5, 4, 6, 5, 2, 6, 3, 4

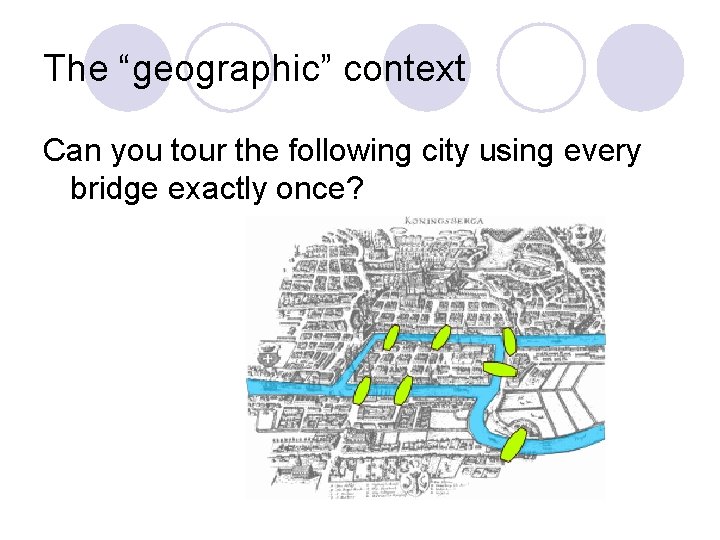
The “geographic” context Can you tour the following city using every bridge exactly once?

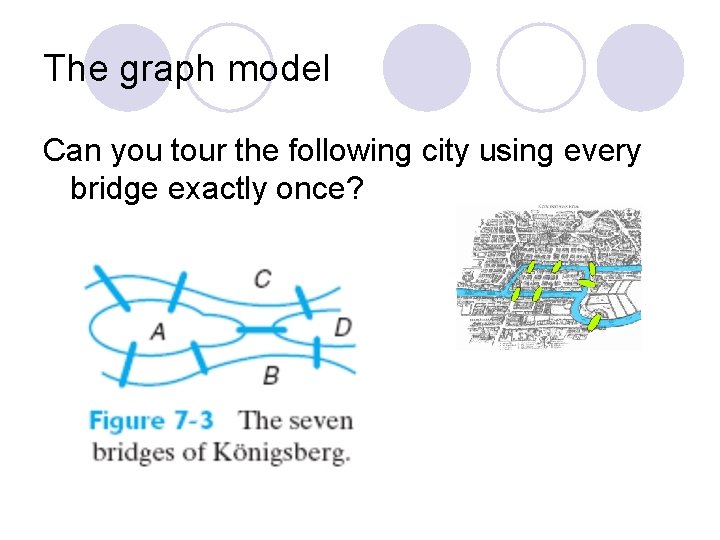
The graph model Can you tour the following city using every bridge exactly once?

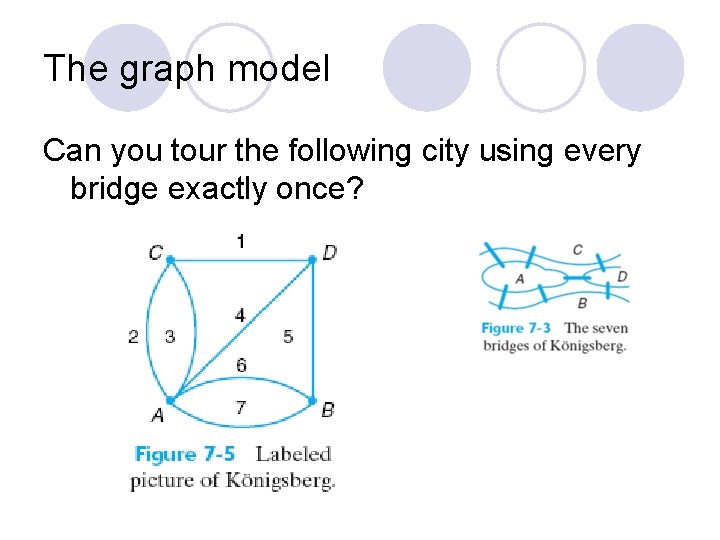
The graph model Can you tour the following city using every bridge exactly once?

Definitions l. A graph consists of vertices (or nodes) and edges connecting pairs of vertices. l A walk is a list v 1, e 1, v 2, e 2, …, vn, where the edges (“e”s) connect the vertices they fall between them. When there are no multiple (parallel) edges, we do not need to list the edges in our description of a walk. A walk is closed if v 1 = vn.

Definitions l. A trail is a walk with no repeated edges, and a closed trail is called a circuit. An Euler trail (or Euler circuit) is one that uses every edge in the graph. l A cycle is a nontrivial circuit in which the only repeated node is the first/last one.

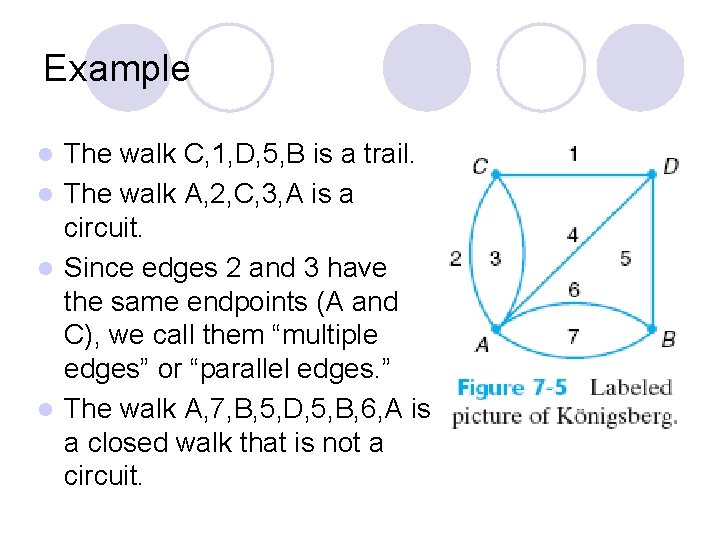
Example The walk C, 1, D, 5, B is a trail. l The walk A, 2, C, 3, A is a circuit. l Since edges 2 and 3 have the same endpoints (A and C), we call them “multiple edges” or “parallel edges. ” l The walk A, 7, B, 5, D, 5, B, 6, A is a closed walk that is not a circuit. l

More terminology l. A loop is an edge that has the same vertex at each end. l The degree of a vertex is the number of edges “coming out” of the vertex. l A simple graph is a graph with no loops or multiple edges. l A graph is connected if between every pair of vertices there is a walk.

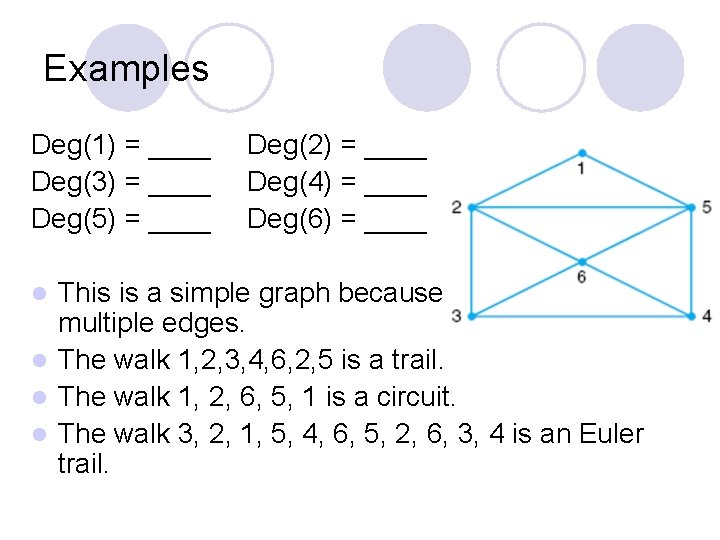
Examples Deg(1) = ____ Deg(3) = ____ Deg(5) = ____ Deg(2) = ____ Deg(4) = ____ Deg(6) = ____ This is a simple graph because it has no loops or multiple edges. l The walk 1, 2, 3, 4, 6, 2, 5 is a trail. l The walk 1, 2, 6, 5, 1 is a circuit. l The walk 3, 2, 1, 5, 4, 6, 5, 2, 6, 3, 4 is an Euler trail. l

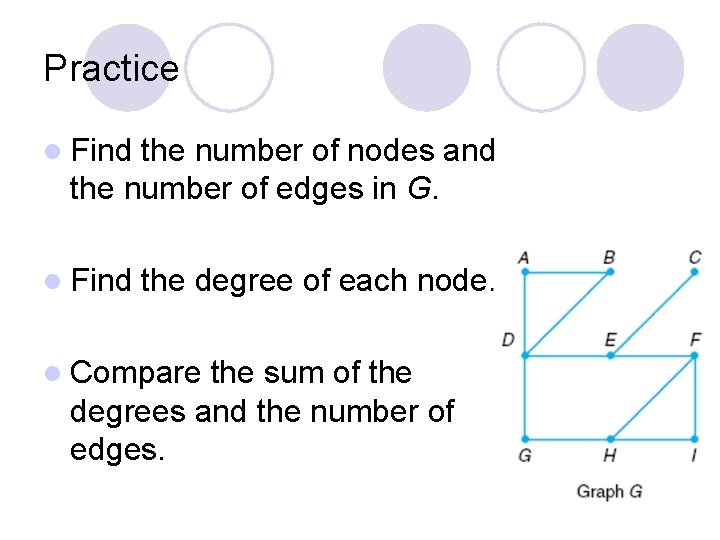
Practice l Find the number of nodes and the number of edges in G. l Find the degree of each node. l Compare the sum of the degrees and the number of edges.

Euler’s result Theorem. If every vertex of a connected graph has even degree, then the graph has an Euler circuit. Corollary. If there are exactly two vertices of odd degree in a connected graph, then the graph has an Euler trail.

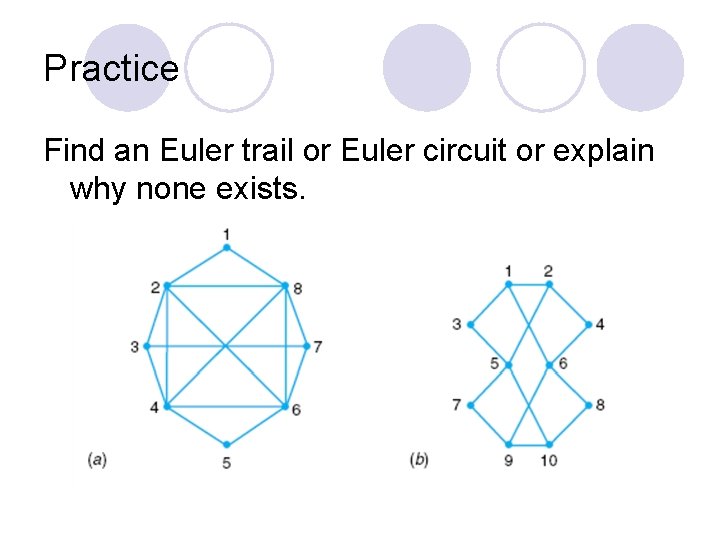
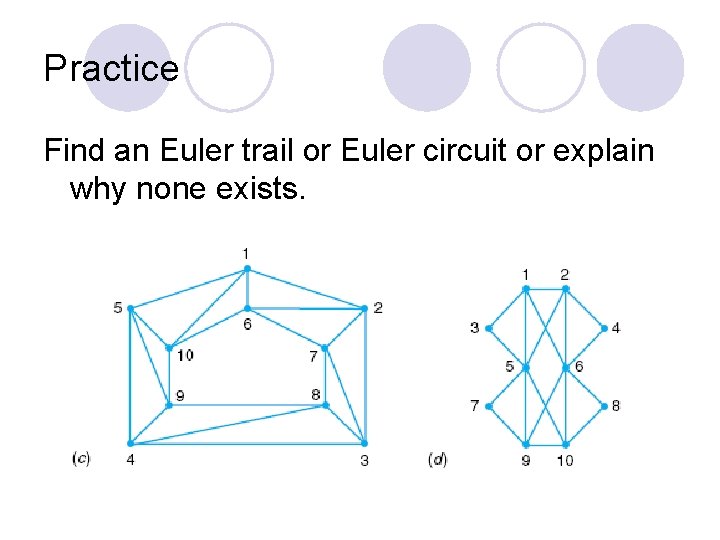
Practice Find an Euler trail or Euler circuit or explain why none exists.

Practice Find an Euler trail or Euler circuit or explain why none exists.

Exercises from Section 7. 1 1 -4, 6 -11, 13 -16