6 Euler Gau Cauchy Leonhard Euler 1707 1783

6. Euler, Gauß, Cauchy

Leonhard Euler (1707 - 1783) Schüler von Johann Bernoulli Größter Mathematiker des 18. Jhd. Fruchtbarster Mathematiker aller Zeiten Sein Werk füllt 70 große Bände Eulersche Winkel (starrer Körper) Eulersche Kreiselgleichung Eulersche Knickgleichung Eulersche Gleichungen (Hydrodynamik) Mondtheorie, Schiffsbau, Artillerie Bezeichnungen am Dreieck eij = cosj + isinj ln(-1) = ip + ik 2 p

Sohn eines Geistlichen, Paul Euler, der dem Unterricht bei Jakob B. zu folgen vermochte. Studium der Theologie und Mathematik. Lieblingsschüler von Johann. B, eng befreundet mit seinen Kommilitonen Niclaus II und Daniel. 1723 Magister Lobende Erwähnung für eine Arbeit über Schiffsbau, obwohl er noch nie ein Schiff auf dem Meer gesehen hatte (mathematisch hervorragend, aber wenig praktisch). Später 12 mal Preisträger. Medizinstudium begonnen, da die Bernouli-Brüder in St. Petersburg über eine vakante Stelle für Med. berichtet hatten. Ruf nach St. Petersburg als Adjunkt für Mathematik, aber Zarin Katharina (nicht die Große) starb am 17. Mai 1727, an dem Tag, als Euler russischen Boden betrat. Peter II. - Euler wird Schiffslieutenant. 1730 Zarin Anna. Euler arbeitet erfolgreich als Akademiker. 1735 Verlust der Sehkraft des rechten Auges. Überanstrengung? 1740 Anna tot. Unruhen. 1741 Zarin Elisabeth schafft Ordnung, aber der berühmte Euler vom neuen König nach Berlin berufen. Dreiwöchige Schiffsreise.

Friedrich II. Zarin Elisabeth

1744 Direktor der math. Klasse der Preuß. Akad. In Berlin über 200 wiss. Arbeiten über Mathematik, Physik, Technik: Populäres Buch: Briefe an eine deutsche Prinzessin. In 7 Sprachen übersetzt. Berlin liegt höher als Magdeburg, weil die Spree in die Havel und diese in die Elbe fließt. - Aber weit unterhalb von Magdeburg!

Friederike von Brandenburg-Schwedt (1745 - 1808)

Bedeutende Preisgelder, fortlaufend Pension aus Rußland. Großes Haus, Landgut, Haushalt mit 18 Personen. Springbrunnen. Übersetzung von russischen Briefen. Griechisch-Lateinisches Quadrat

Griechisch-Lateinische Quadrate Griechisch-Lateinisches 6*6 -Quadrat weder gefunden, noch Nichtexistenz beweisen können. Allgemeine Untersuchung: Es gibt GL-Quadrate für jede ungerade Basis und für jede durch 4 teilbare Basis. Unbekannt bleiben die Basen 2 n + 2 = {2, 6, 10, . . . } Griechisch-Lateinisches 2*2 -Quadrat existiert nicht: Euler vermutete: (2 n + 2)-GL-Quadrate existieren nicht. Gaston Tarry 1900: alle 6*6 -Quadrate durchmustert. Vermutung stimmt. 1959 GL-Quadrat zur Basis 22 konstruiert. Später bewiesen: außer zur Basis 2 und zur Basis 6 existieren alle.

Bedeutende Preisgelder, fortlaufend Pension aus Rußland. Großes Haus, Landgut, Haushalt mit 18 Personen. Springbrunnen. Übersetzung von russischen Briefen. Griechisch-Lateinisches Quadrat. Vermessungen zur Trockenlegung des Oderbruchs. Berechnungen zu Renten. Friedrich erkannte Eulers französische Gelehrte vor. Größe nicht, zog

Dort auch p (eingeführt von Jones) verwandt.

Wagte sich auch an metaphysische Fragen, wo bei Voltaire und andere gelehrte Schwätzer ihn oft aufs Glatteis führten. 1766 Triumphale Rückkehr nach St. Petersburg. Erblindet. Kurz vorher noch blind zu schreiben geübt Staroperation zunächst erfolgreich, dann Infektion Bis zum Tode produktiv. Oft mit einem Enkel auf dem Schoß. Hunderte von Publikationen unter Mithilfe von Assistenten. Kopfrechnen und Gedächtnis phänomenal. Das Rechnen fällt ihm so leicht wie anderen das Atmen. [F. Arago] 1783 Schlaganfall Größter Mathematiker des 18. Jhd. Fruchtbarster Mathematiker aller Zeiten. Arbeiten aufgestapelt. Bei Bedarf gedruckt. Oft die Ergänzungen vor den Originalen.

Johann B: mathematicorum princeps d'Alembert: Ce diable d'homme Königsberger Brückenproblem (1741): Ist es möglich, alle sieben Brücken über den Pregel einmal zu passieren, ohne eine zweimal zu benutzen?

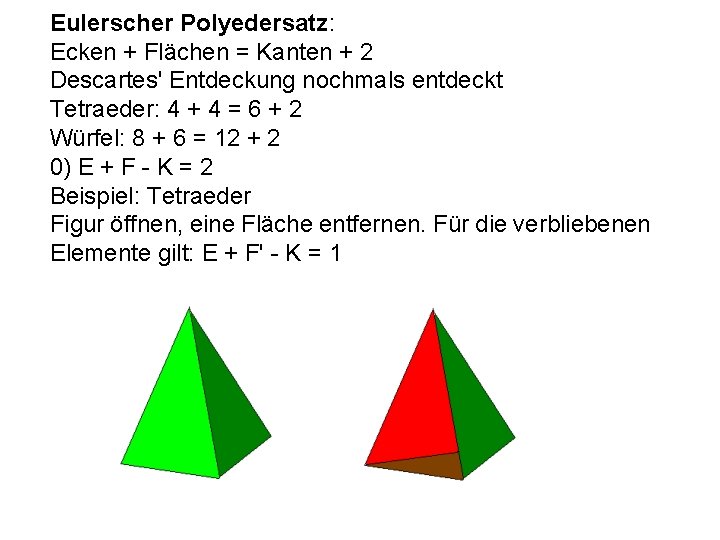
Eulerscher Polyedersatz: Ecken + Flächen = Kanten + 2 Descartes' Entdeckung nochmals entdeckt Tetraeder: 4 + 4 = 6 + 2 Würfel: 8 + 6 = 12 + 2 0) E + F - K = 2 Beispiel: Tetraeder Figur öffnen, eine Fläche entfernen. Für die verbliebenen Elemente gilt: E + F' - K = 1

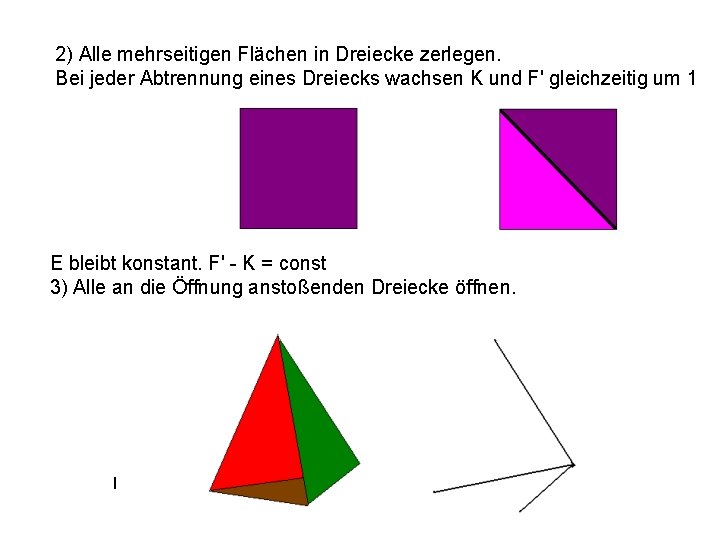
2) Alle mehrseitigen Flächen in Dreiecke zerlegen. Bei jeder Abtrennung eines Dreiecks wachsen K und F' gleichzeitig um 1 E bleibt konstant. F' - K = const 3) Alle an die Öffnung anstoßenden Dreiecke öffnen.

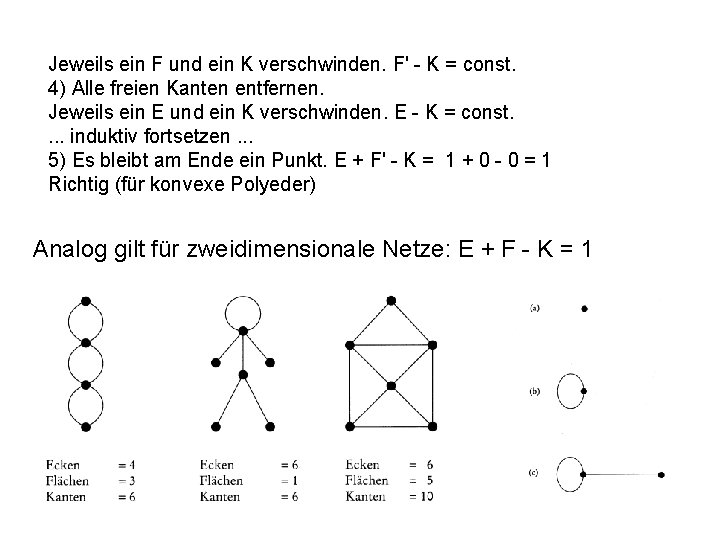
Jeweils ein F und ein K verschwinden. F' - K = const. 4) Alle freien Kanten entfernen. Jeweils ein E und ein K verschwinden. E - K = const. . induktiv fortsetzen. . . 5) Es bleibt am Ende ein Punkt. E + F' - K = 1 + 0 - 0 = 1 Richtig (für konvexe Polyeder) Analog gilt für zweidimensionale Netze: E + F - K = 1

Zetafunktion Ausgehend von der Reihe für sin x die Reihe der inversen Quadrate summiert (Leibniz und die Bernoullis hatten es vergeblich versucht) z(2) = 1 + 1/22 + 1/32 + 1/42 +. . . = p 2/6 z(4) = 1 + 1/24 + 1/34 + 1/44 +. . . = p 4/90. . .

für a 0 ≠ 0

Vergleich der quadratischen Glieder liefert

Zetafunktion Ausgehend von der Reihe für sin x die Reihe der inversen Quadrate summiert (Leibniz und die Bernoullis hatten es vergeblich versucht) z(2) = 1 + 1/22 + 1/32 + 1/42 +. . . = p 2/6 z(4) = 1 + 1/24 + 1/34 + 1/44 +. . . = p 4/90. . . Reihenwerte für ungerade Potenzen: vergeblich gesucht bislang noch nicht gefunden z(-1) = 1 + 2 + 3 + 4 +. . . = -1/12

für alle x mit |x| < 1 für x = 1

Die Anzahl der Primzahlen p < N ist ungefähr lnln. N Euler fand die längste Primzahlfolge: n(n+1) + 41 liefert Primzahlen für n = 0 bis n = 39 41, 43, 47, 53, 61, 71, 83, 97. . . Euler hat, wie seine Zeitgenossen, divergente Reihen bedenkenlos eingesetzt, gibt aber erstmals ein Konvergenz-kriterium an: Der Reihenrest nach dem "unendlichsten" Glied muß unendlich klein werden. Euler schreibt immer das letzte Glied mit hin, meist i für numerus infinitus.

= x 0 + x 1 + x 2 + x 3 +. . . + xi = (-1)0 + (-1)1 + (-1)2 + (-1)3 +. . . = 1 - 1 + -. . . = ½ auch Leibniz und Jakob B. kamen zu diesem Schluß = 1 + 2 + 4 + 8 +. . . = -1 mit Wallis angenommen: 1/3 < 1/2 < 1/1 < 1/0 < 1/-1

ln(a/b) = lna - lnb ln 2 = ln 2 - ln -1 - 1/2 - 1/3 -. . . - 1/

Carl Friedrich Gauß (1777 - 1855) Der dreijährige Carl Friedrich korrigierte seinen Vater bei der Lohnabrechnung. Rechnen vor dem Sprechen gelernt. Mit neun Jahren: 1 + 2 + 3 +. . . + 100 + 99 + 98 +. . . + = 5050 1 101 +. . . + 101 1 + 2 + 3 +. . . + n = n(n+1)/2 = 10100

Disquisitiones Arithmeticae (1801) Zahlentheorie Modulo-Arithmetik Satz von Fermat Satz von Wilson Quadratische Gleichungen Quadratische Formen Primzahltests Kreisteilung

Konstruktion des 17 -Eck Algebra Methode der kleinsten Quadrate Fehlerfortpflanzungsgesetz Osterformel Eliminationsverfahren Nichteuklidische Geometrie Beweis des Fundamentalsatzes der Algebra Krümmung (1/r) Elliptische Integrale Arithmetisch-geometrisches Mittel: a 0, b 0 > 0 an+1 = (an + bn)/2 bn+1 = /anbn

Wiederauffindung des Ceres Kirchhoffsche Gesetze Erdvermessung Erdmagnetfeld Telegraph Heliotrop Direktor der Göttinger Sternwarte Er vermaß […] ein durch drei Berge, den Brocken, den Hohen Hagen und den Inselberg gebildetes Dreieck, dessen Seiten 69, 85 und 107 km maßen. Es braucht kaum eigens gesagt zu werden, daß er innerhalb der Fehlergrenze keine Abweichung von 180° entdeckte und daraus den Schluß zog, die Struktur des wirklichen Raumes sei, soweit die Erfahrung darüber eine Aussage erlaubt, Euklidisch

Pauca sed matura Komplexe Zahlenebene Gedenkmünze „Mathematicorum Principi“ 170000 Taler Vermögen Jahresgrundgehalt eines Prof. 1000 Taler

Tätigkeit als Ingenieur ab 1816 Professor in Frankreich und Italien Mit etwa 800 Abhandlungen ungewöhnlich produktiver und vielseitiger Mathematiker Cauchy-Kriterium Quotientenkriterium Wurzelkriterium Reihenverdichtung Konvergenzradius Diagonalverfahren Ableitung und Integral als Grenzwert Theorie komplexer Funktionen Augustin Louis Cauchy (1789 - 1857) n |Sak| < e k=m

Potentielles Verständnis des Grenzwertes: Wenn die Werte, die eine Variable annimmt, unbeschränkt einem festem Wert zustreben, so dass sie schließlich von ihm so wenig abweichen wie man will, so wird derselbe der Grenzwert aller anderen genannt. Irrationale Zahlen lassen sich als Grenzwerte von Folgen rationaler Zahlen definieren. x = a a x 2 = a 2 x 2 = x 2 +