From APW to LAPW to LAPWlo Karlheinz Schwarz

From APW to LAPW to (L)APW+lo Karlheinz Schwarz Institute for Material Chemistry TU Wien Vienna University of Technology

Atomic scale and quantum mechanics n An understanding of the electronic structure requires n quantum mechanical treatment of the electrons in the presence of nuclei n n n Crystal structure n Periodic boundary conditions n n n Unit cells Clusters Size n n n Hartree Fock (exchange) plus correlation Density Functional Theory (DFT) A few atoms per unit cell (to about 100) Large unit cells (for a simulation of e. g. impurities) Computational demand n n n CPU time (efficiency, high through-put, parallel) available software (portability) WIEN 2 k Hardware (PCs, cluster of PCs, workstations, supercomputers)

A few solid state concepts n Crystal structure Unit cell (defined by 3 lattice vectors) leading to 7 crystal systems n Bravais lattice (14) n Atomic basis (Wyckoff position) n Symmetries (rotations, inversion, mirror planes, glide plane, screw axis) n Space group (230) n Wigner-Seitz cell n Reciprocal lattice (Brillouin zone) n n Electronic structure Periodic boundary conditions n Bloch theorem (k-vector), Bloch function n Schrödinger equation (HF, DFT) n

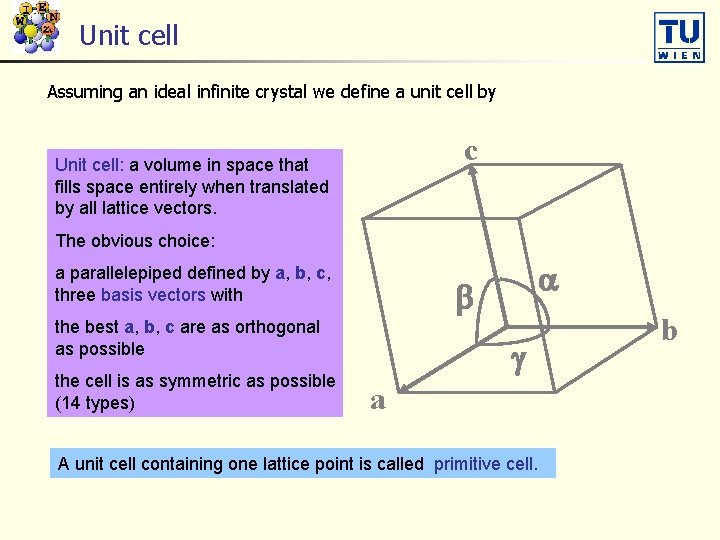
Unit cell Assuming an ideal infinite crystal we define a unit cell by c Unit cell: a volume in space that fills space entirely when translated by all lattice vectors. The obvious choice: a parallelepiped defined by a, b, c, three basis vectors with b the best a, b, c are as orthogonal as possible the cell is as symmetric as possible (14 types) a g a A unit cell containing one lattice point is called primitive cell. b

Wigner-Seitz Cell Form connection to all neighbors and span a plane normal to the connecting line at half distance

Bloch-Theorem: V(x) has lattice periodicity (“translational invariance”): V(x)=V(x+a) The electron density (x) has also lattice periodicity, however, the wave function does NOT: Application of the translation t g-times:

periodic boundary conditions: n The wave function must be uniquely defined: after G translations it must be identical (G a: periodicity volume): a Ga

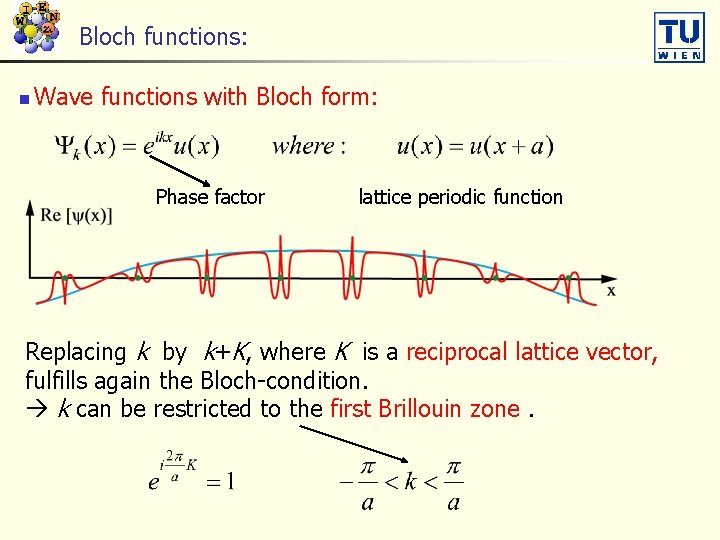
Bloch functions: n Wave functions with Bloch form: Phase factor lattice periodic function Replacing k by k+K, where K is a reciprocal lattice vector, fulfills again the Bloch-condition. k can be restricted to the first Brillouin zone.

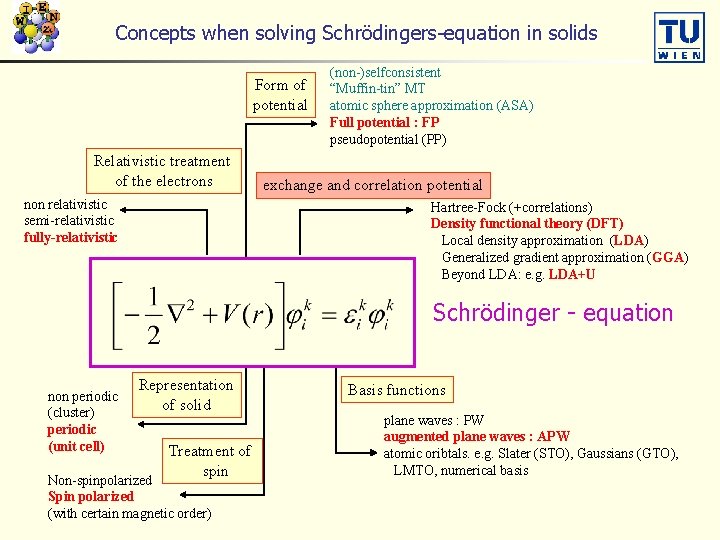
Concepts when solving Schrödingers-equation in solids Form of potential Relativistic treatment of the electrons non relativistic semi-relativistic fully-relativistic (non-)selfconsistent “Muffin-tin” MT atomic sphere approximation (ASA) Full potential : FP pseudopotential (PP) exchange and correlation potential Hartree-Fock (+correlations) Density functional theory (DFT) Local density approximation (LDA) Generalized gradient approximation (GGA) Beyond LDA: e. g. LDA+U Schrödinger - equation non periodic (cluster) periodic (unit cell) Representation of solid Treatment of spin Non-spinpolarized Spin polarized (with certain magnetic order) Basis functions plane waves : PW augmented plane waves : APW atomic oribtals. e. g. Slater (STO), Gaussians (GTO), LMTO, numerical basis

DFT Density Functional Theory Hohenberg-Kohn theorem: (exact) The total energy of an interacting inhomogeneous electron gas in the presence of an external potential Vext(r ) is a functional of the density Kohn-Sham: (still exact!) Ekinetic non interacting Ene Ecoulomb Eee Exc exchange-correlation In KS the many body problem of interacting electrons and nuclei is mapped to a one-electron reference system that leads to the same density as the real system.

Kohn-Sham equations LDA, GGA vary 1 -electron equations (Kohn Sham) -Z/r LDA treats both, exchange and correlation effects, GGA but approximately New (better ? ) functionals are still an active field of research

Walter Kohn, Nobel Prize 1998 Chemistry “Self-consistent Equations including Exchange and Correlation Effects” W. Kohn and L. J. Sham, Phys. Rev. 140, A 1133 (1965) Literal quote from Kohn and Sham’s paper: “… We do not expect an accurate description of chemical binding. ”

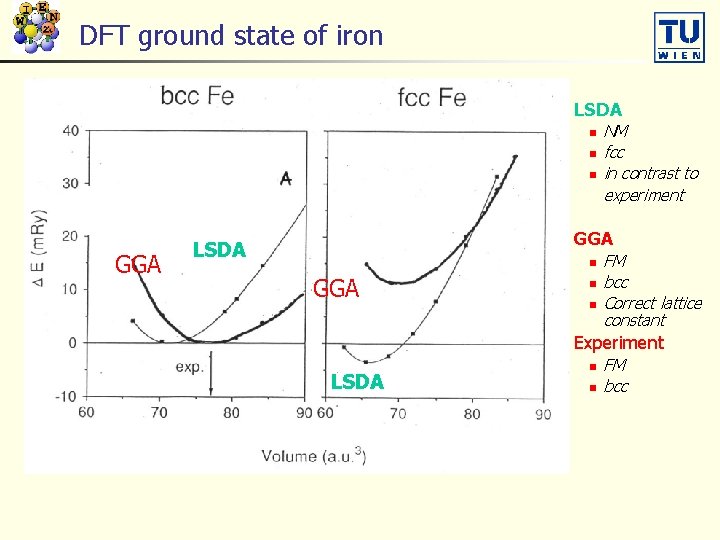
DFT ground state of iron n LSDA n n n GGA n LSDA GGA n n n LSDA NM fcc in contrast to experiment FM bcc Correct lattice constant Experiment n n FM bcc

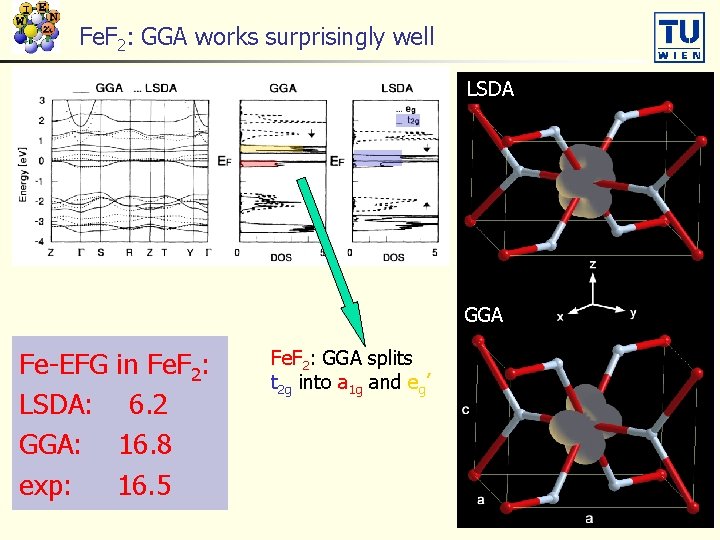
Fe. F 2: GGA works surprisingly well LSDA GGA Fe-EFG LSDA: GGA: exp: in Fe. F 2: 6. 2 16. 8 16. 5 Fe. F 2: GGA splits t 2 g into a 1 g and eg’

Solving Schrödingers equation: Y cannot be found analytically n complete “numerical” solution is possible but inefficient n Ansatz: n n linear combination of some “basis functions” n n n different methods use different basis sets ! finding the “best” wave function using the variational principle: this leads to the famous “Secular equations”, i. e. a set of linear equations which in matrix representation is called “generalized eigenvalue problem” HC=ESC H, S : hamilton and overlap matrix; C: eigenvectors, E: eigenvalues

Basis Sets for Solids plane waves (pseudo potentials) n space partitioning (augmentation) methods n n LMTO (linear muffin tin orbitals) ASA approx. , linearized numerical radial function + Hankel- and Bessel function expansions n n ASW (augmented spherical wave) n n FP-LMTO (full-potential LMTO) n n solution of multiple scattering problem, Greens function formalism equivalent to APW (L)APW (linearized augmented plane waves) LCAO methods n n similar to LAPW, space partitioned with non-overlapping spheres KKR (Kohn, Koringa, Rostocker method) n n similar to LMTO Gaussians, Slater, or numerical orbitals, often with PP option) See talk by Jörg Behler (Saturday) for comparison of methods

pseudopotential plane wave methods plane waves form a “complete” basis set, however, they “never” converge due to the rapid oscillations of the atomic wave functions close to the nuclei l let´s get rid of all core electrons and these oscillations by replacing the strong ion–electron potential by a much weaker (and physically dubious) l pseudopotential l Hellmann´s 1935 combined approximation method

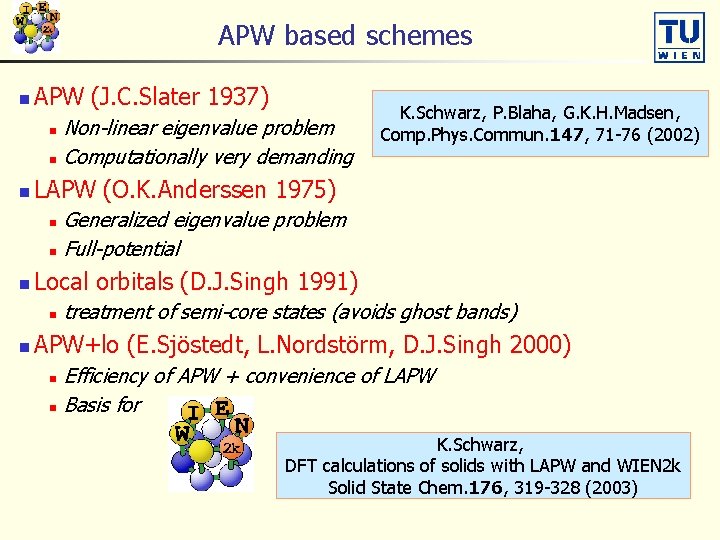
APW based schemes n APW (J. C. Slater 1937) Non-linear eigenvalue problem n Computationally very demanding n n K. Schwarz, P. Blaha, G. K. H. Madsen, Comp. Phys. Commun. 147, 71 -76 (2002) LAPW (O. K. Anderssen 1975) Generalized eigenvalue problem n Full-potential n n Local orbitals (D. J. Singh 1991) n n treatment of semi-core states (avoids ghost bands) APW+lo (E. Sjöstedt, L. Nordstörm, D. J. Singh 2000) Efficiency of APW + convenience of LAPW n Basis for n K. Schwarz, DFT calculations of solids with LAPW and WIEN 2 k Solid State Chem. 176, 319 -328 (2003)

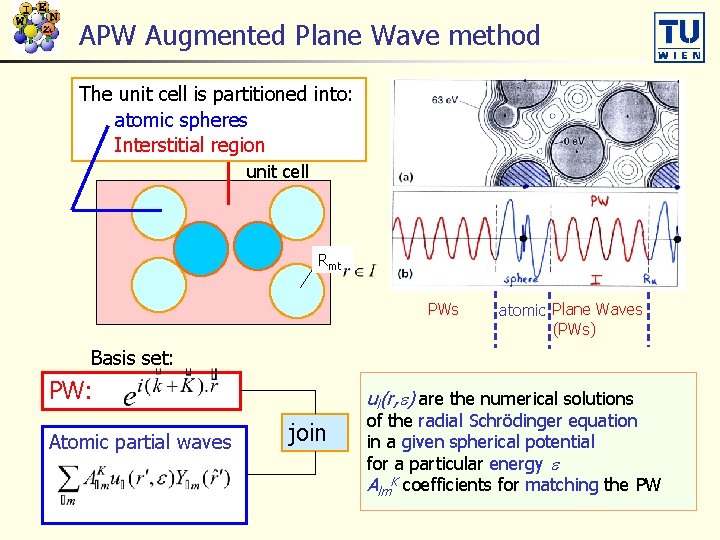
APW Augmented Plane Wave method The unit cell is partitioned into: atomic spheres Interstitial region unit cell Rmt PWs atomic Plane Waves (PWs) Basis set: PW: Atomic partial waves ul(r, e) are the numerical solutions join of the radial Schrödinger equation in a given spherical potential for a particular energy e Alm. K coefficients for matching the PW

Numerical solution of the radial Schrödinger equation n n Assuming a spherically symmetric potential we can use the Ansatz: This leads to the radial Schrödinger equation:

numerical calculation of P’’ assume an equidistant radial mesh (h=rn+1 -rn; yn=y(rn)) n replace 2 nd derivative by 2 nd differences d 2: yn 1 st diff. 2 nd diff. yn+1 yn-1 n rn-1 h rn+1 n Taylor-expansion of yn at rn:

Numerov method By a clever Ansatz one can find even better agreement: n Ansatz: n n substitute this Ansatz into the previous result:

Recursion formula: n The Numerov solution yields a recursion formula for P: n P(r) = R(r). r n solve P for given ℓ, V and E n the first two points from P(0)=0 and P~rℓ n (today even faster and more accurate solvers are available) and g(r)=ℓ(ℓ+1)/r 2 + V(r) – E

Slater‘s APW (1937) Atomic partial waves H Hamiltonian S overlap matrix Energy dependent basis functions lead to a Non-linear eigenvalue problem Numerical search for those energies, for which the det|H-ES| vanishes. Computationally very demanding. “Exact” solution for given MT potential!

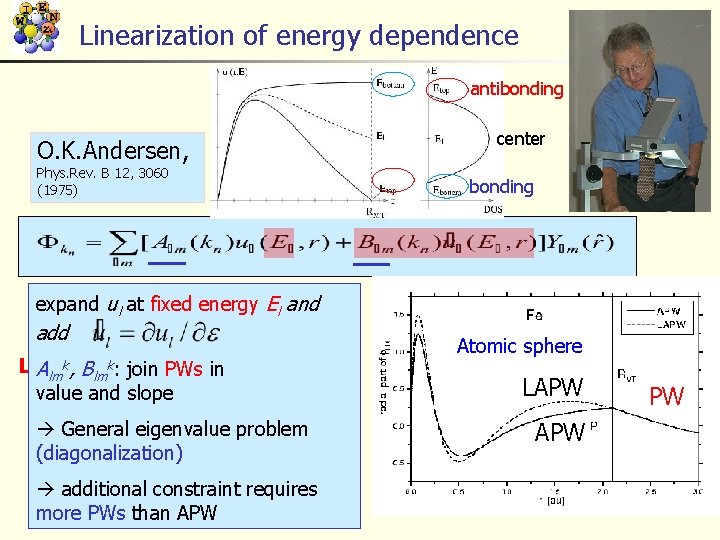
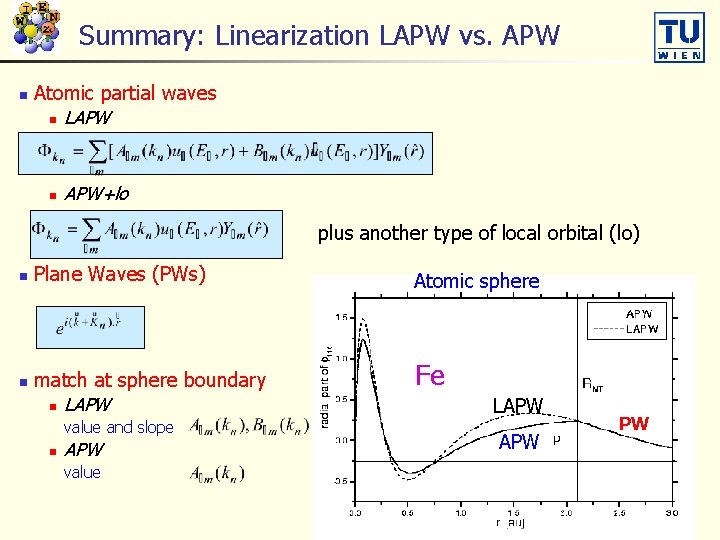
Linearization of energy dependence antibonding O. K. Andersen, Phys. Rev. B 12, 3060 (1975) center bonding expand ul at fixed energy El and add k LAPW by Almk, Bsuggested lm : join PWs in value and slope General eigenvalue problem (diagonalization) additional constraint requires more PWs than APW Atomic sphere LAPW PW

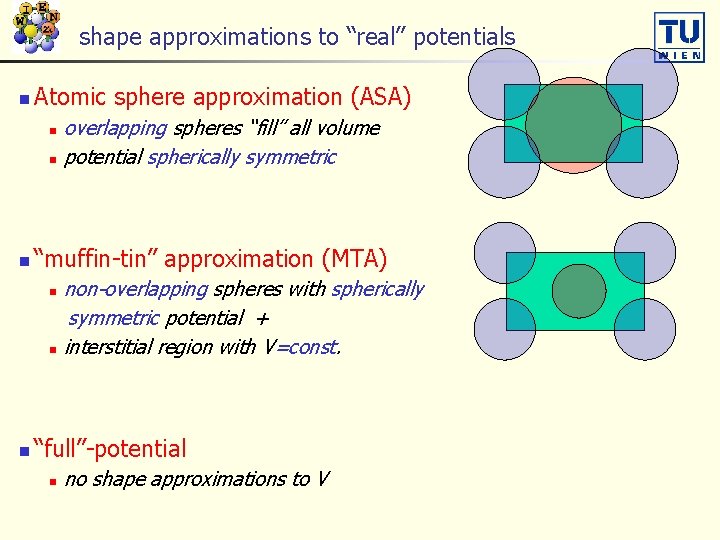
shape approximations to “real” potentials n Atomic sphere approximation (ASA) overlapping spheres “fill” all volume n potential spherically symmetric n n “muffin-tin” approximation (MTA) non-overlapping spheres with spherically symmetric potential + n interstitial region with V=const. n n “full”-potential n no shape approximations to V

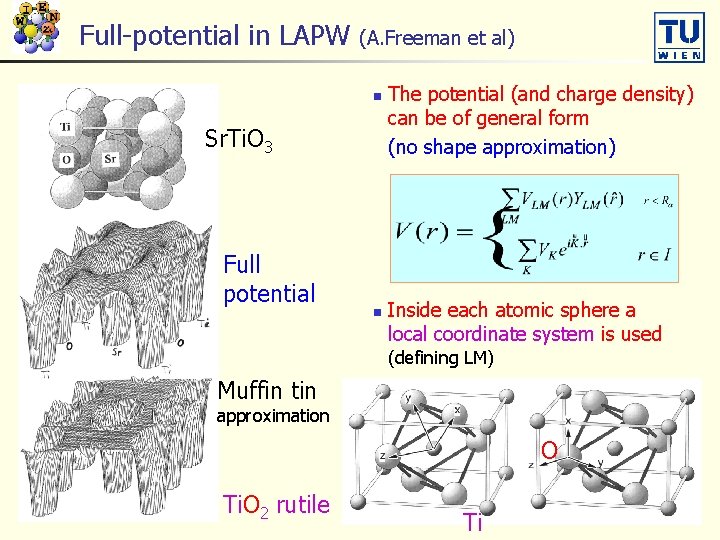
Full-potential in LAPW (A. Freeman et al) n Sr. Ti. O 3 Full potential n The potential (and charge density) can be of general form (no shape approximation) Inside each atomic sphere a local coordinate system is used (defining LM) Muffin tin approximation O Ti. O 2 rutile Ti

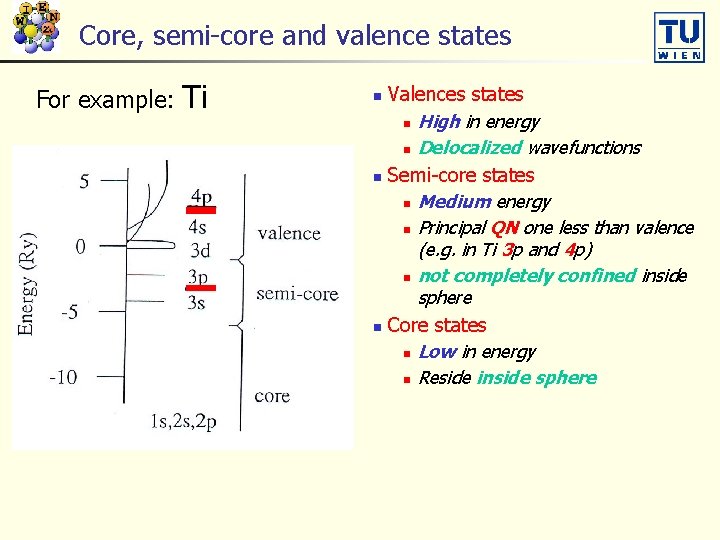
Core, semi-core and valence states For example: Ti Valences states n High in energy n Delocalized wavefunctions n Semi-core states n Medium energy n Principal QN one less than valence (e. g. in Ti 3 p and 4 p) n not completely confined inside sphere n Core states n Low in energy n Reside inside sphere n

Semi-core problems in LAPW Problems with semi-core states

Local orbitals (LO) n Ti atomic sphere LOs n are confined to an atomic sphere n have zero value and slope at R n Can treat two principal QN n for each azimuthal QN ( e. g. 3 p and 4 p) n Corresponding states are strictly orthogonal n n n (e. g. semi-core and valence) Tail of semi-core states can be represented by plane waves Only slightly increases the basis set (matrix size) D. J. Singh, Phys. Rev. B 43 6388 (1991)

The LAPW + LO method The LAPW+LO basis is: (r) = -1/2 c. K ei(K+k) r { (A lm K lmul(r)+Blmůl(r)) Ylm(r) + clm(A’lmul(r)+B’lmůl(r)+u(2)l(r)) Ylm(r) lm The variational coefficients are: (1) c. K and (2) clm Subsidiary (non-variational) coefficients are Alm Blm A’lm & B’lm • Alm and Blm are determined by matching the value and derivative on the sphere boundary to the plane waves as usual. • A’lm and B’lm are determined by forcing the value and derivative of the LO on the sphere boundary to zero. The part (A’lmul(r)+B’lmůl(r)+u(2)l(r)) Ylm(r) is formally a local orbital.

The LAPW + LO method Key Points: 1. The local orbitals should only be used for those atoms and angular momenta, for which they are needed. K 2. The local orbitals are just another way to handle the augmentation. They look very different from atomic functions. 3. We are trading a large number LO of extra plane wave coefficients for some clm. Shape of H and S <K|K>

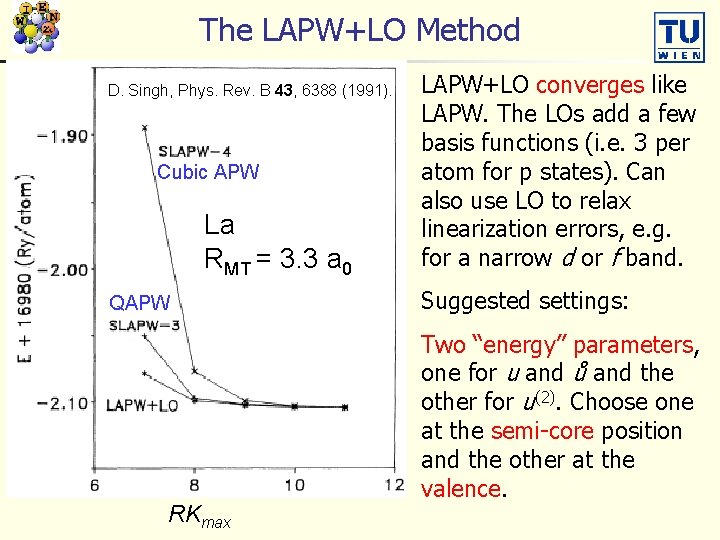
The LAPW+LO Method D. Singh, Phys. Rev. B 43, 6388 (1991). Cubic APW La RMT = 3. 3 a 0 QAPW RKmax LAPW+LO converges like LAPW. The LOs add a few basis functions (i. e. 3 per atom for p states). Can also use LO to relax linearization errors, e. g. for a narrow d or f band. Suggested settings: Two “energy” parameters, one for u and ů and the other for u(2). Choose one at the semi-core position and the other at the valence.

An alternative combination of schemes E. Sjöstedt, L. Nordström, D. J. Singh, An alternative way of linearizing the augmented plane wave method, Solid State Commun. 114, 15 (2000) • Use APW, but at fixed El (superior PW convergence) • Linearize with additional local orbitals (lo) (add a few extra basis functions) optimal solution: mixed basis • use APW+lo for states which are difficult to converge: (f or d- states, atoms with small spheres) • use LAPW+LO for all other atoms and angular momenta

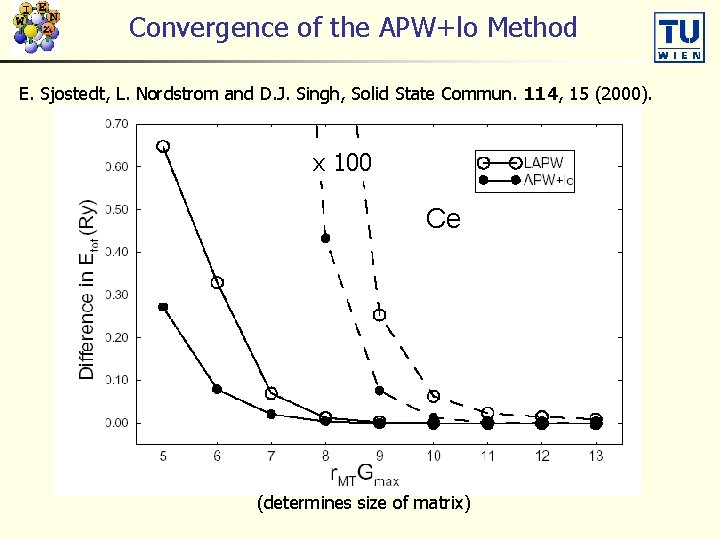
Convergence of the APW+lo Method E. Sjostedt, L. Nordstrom and D. J. Singh, Solid State Commun. 114, 15 (2000). x 100 Ce (determines size of matrix)

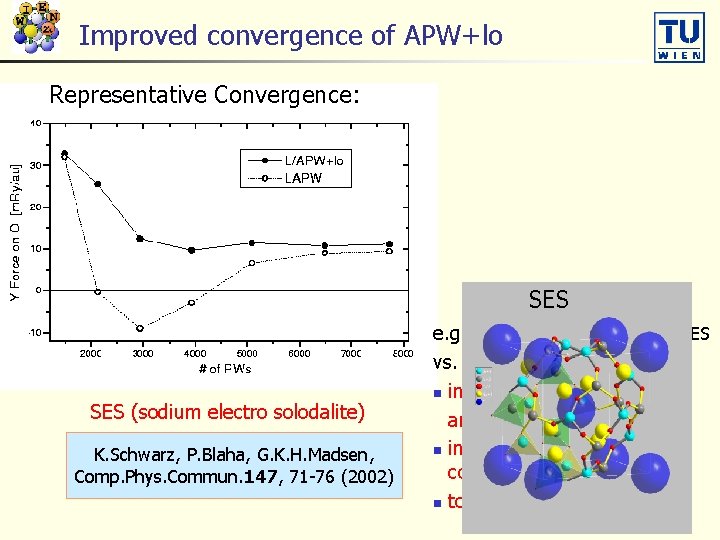
Improved convergence of APW+lo Representative Convergence: SES (sodium electro solodalite) K. Schwarz, P. Blaha, G. K. H. Madsen, Comp. Phys. Commun. 147, 71 -76 (2002) e. g. force (Fy) on oxygen in SES vs. # plane waves: n in LAPW changes sign and converges slowly n in APW+lo better convergence n to same value as in LAPW

Summary: Linearization LAPW vs. APW n Atomic partial waves n LAPW n APW+lo plus another type of local orbital (lo) n n Plane Waves (PWs) Atomic sphere match at sphere boundary n LAPW Fe value and slope n APW value LAPW PW

Method implemented in WIEN 2 k E. Sjöststedt, L. Nordström, D. J. Singh, SSC 114, 15 (2000) • Use APW, but at fixed El (superior PW convergence) • Linearize with additional lo (add a few basis functions) optimal solution: mixed basis • use APW+lo for states which are difficult to converge: (f- or d- states, atoms with small spheres) • use LAPW+LO for all other atoms and angular momenta A summary is given in K. Schwarz, P. Blaha, G. K. H. Madsen, Comp. Phys. Commun. 147, 71 -76 (2002)

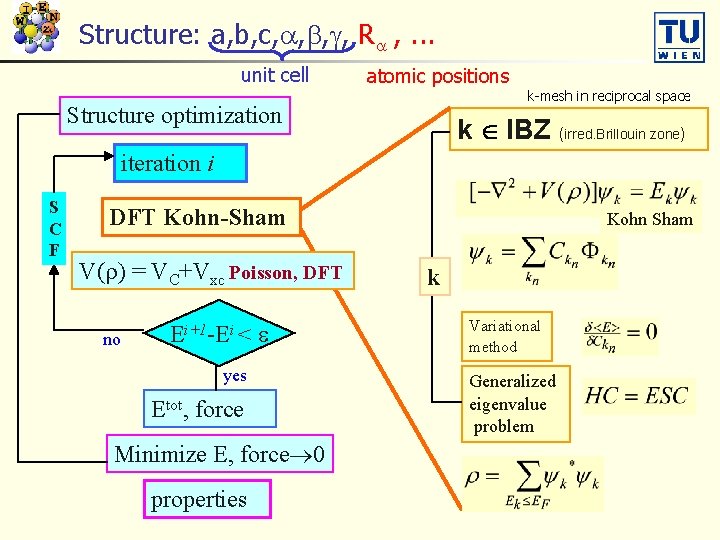
Structure: a, b, c, , R , . . . unit cell atomic positions Structure optimization k-mesh in reciprocal space k IBZ (irred. Brillouin zone) iteration i S C F DFT Kohn-Sham V( ) = VC+Vxc Poisson, DFT no Ei+1 -Ei < yes Etot, force Minimize E, force 0 properties Kohn Sham k Variational method Generalized eigenvalue problem

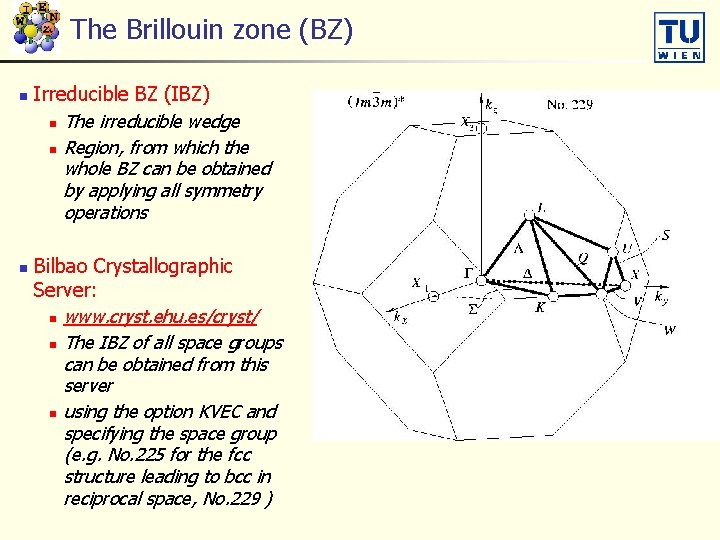
The Brillouin zone (BZ) n n Irreducible BZ (IBZ) n The irreducible wedge n Region, from which the whole BZ can be obtained by applying all symmetry operations Bilbao Crystallographic Server: n www. cryst. ehu. es/cryst/ n The IBZ of all space groups can be obtained from this server n using the option KVEC and specifying the space group (e. g. No. 225 for the fcc structure leading to bcc in reciprocal space, No. 229 )

Self-consistent field (SCF) calculations In order to solve HY=EY we need to know the potential V(r) n for V(r) we need the electron density (r) n the density (r) can be obtained from Y(r)*Y(r) n ? ? Y(r) is unknown before HY=EY is solved ? ? n Start with rin(r) Do the mixing of r(r) Calculate Veff (r) =f[r(r)] SCF cycles

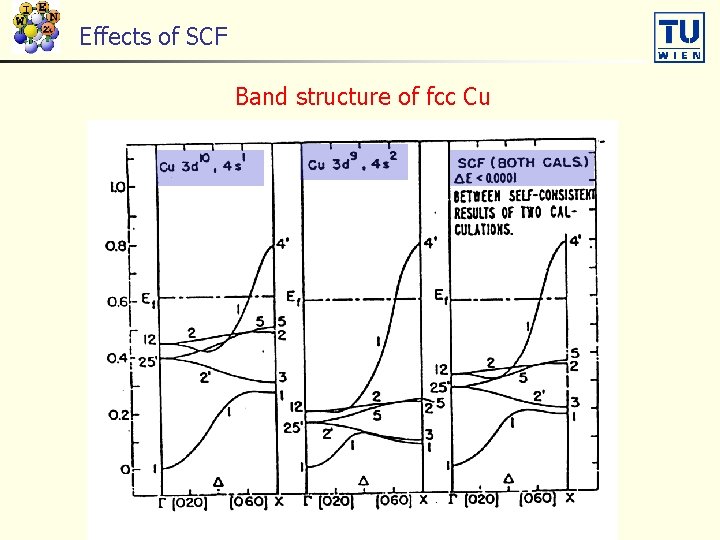
Effects of SCF Band structure of fcc Cu

WIEN 2 k software package An Augmented Plane Wave Plus Local Orbital Program for Calculating Crystal Properties Peter Blaha Karlheinz Schwarz Georg Madsen Dieter Kvasnicka Joachim Luitz WIEN 2 k: ~850 groups worldwide Based on DFT-LDA (GGA) Accuracy determined by one parameter: number of PW November 2001 Vienna, AUSTRIA Vienna University of Technology http: //www. wien 2 k. at

The WIEN 2 k authors G. Madsen P. Blaha K. Schwarz D. Kvasnicka J. Luitz

Main developers of WIEN 2 k n Authors of WIEN 2 k P. Blaha, K. Schwarz, D. Kvasnicka, G. Madsen and J. Luitz Other contributions to WIEN 2 k n C. Ambrosch-Draxl (Univ. Graz, Austria), optics n U. Birkenheuer (Dresden), wave function plotting n R. Dohmen und J. Pichlmeier (RZG, Garching), parallelization n C. Först (Vienna), afminput n R. Laskowski (Vienna), non-collinear magnetism n P. Novák and J. Kunes (Prague), LDA+U, SO n B. Olejnik (Vienna), non-linear optics n C. Persson (Uppsala), irreducible representations n M. Scheffler (Fritz Haber Inst. , Berlin), forces, optimization n D. J. Singh (NRL, Washington D. C. ), local orbitals (LO), APW+lo n E. Sjöstedt and L Nordström (Uppsala, Sweden), APW+lo n J. Sofo and J. Fuhr (Penn State, USA), Bader analysis n B. Yanchitsky and A. Timoshevskii (Kiev), space group n and many others …. n

International users n More than 850 user groups worldwide 30 industries (Canon, Eastman, Exxon, Fuji, Hitachi, Idemitsu Petroch. , A. D. Little, Mitsubishi, Motorola, NEC, Nippon Steel, Norsk Hydro, Osram, Panasonic, Samsung, Siemens, Sony, Sumitomo, TDK, Toyota). n Europe: A, B, CH, CZ, D, DK, ES, F, FIN, GR, H, I, IL, IRE, N, NL, PL, RO, S, SK, SL, UK, (EHT Zürich, MPI Stuttgart, FHI Berlin, DESY, TH Aachen, ESRF, Prague, Paris, Chalmers, Cambridge, Oxford) n America: ARG, BZ, CDN, MX, USA (MIT, NIST, Berkeley, Princeton, Harvard, Argonne NL, Los Alamos NL, Penn State, Georgia Tech, Lehigh, Chicago, Stony Brook, SUNY, UC St. Barbara, Toronto) n far east: AUS, China, India, JPN, Korea, Pakistan, Singapore, Taiwan (Beijing, Tokyo, Osaka, Kyoto, Sendai, Tsukuba, Hong Kong) n

Vienna city of music and the WIEN 2 k code Thank you for your attention