Fin 501 Asset Pricing Overview Simple CAPM with

Fin 501: Asset Pricing Overview • Simple CAPM with quadratic utility functions (derived from state-price beta model) • Mean-variance preferences – Portfolio Theory – CAPM (traditional derivation) • With risk-free bond • Zero-beta CAPM • CAPM (modern derivation) – Projections – Pricing Kernel and Expectation Kernel Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

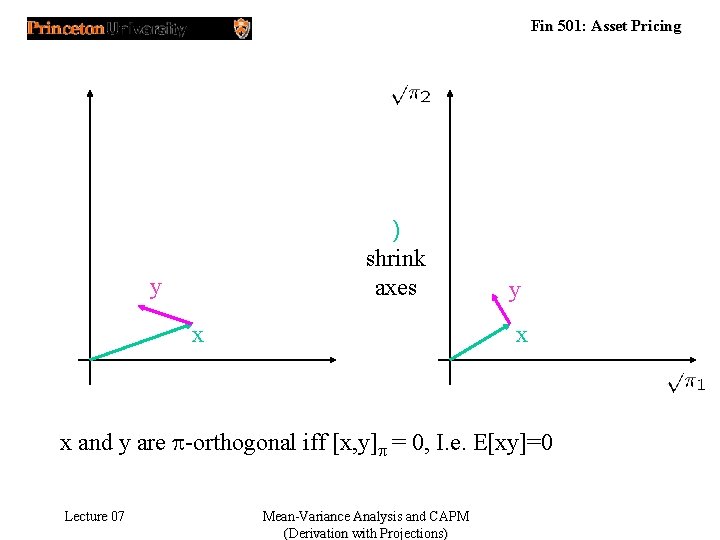
Fin 501: Asset Pricing Projections • States s=1, …, S with ps >0 • Probability inner product • p-norm Lecture 07 (measure of length) Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing ) shrink axes y x x and y are p-orthogonal iff [x, y]p = 0, I. e. E[xy]=0 Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing …Projections… • Z space of all linear combinations of vectors z 1, …, zn • Given a vector y 2 RS solve • [smallest distance between vector y and Z space] Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing …Projections y e y. Z E[e zj]=0 for each j=1, …, n (from FOC) e? z y. Z is the (orthogonal) projection on Z Z + e’ , y. Z 2 Z, e ? z y = y Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

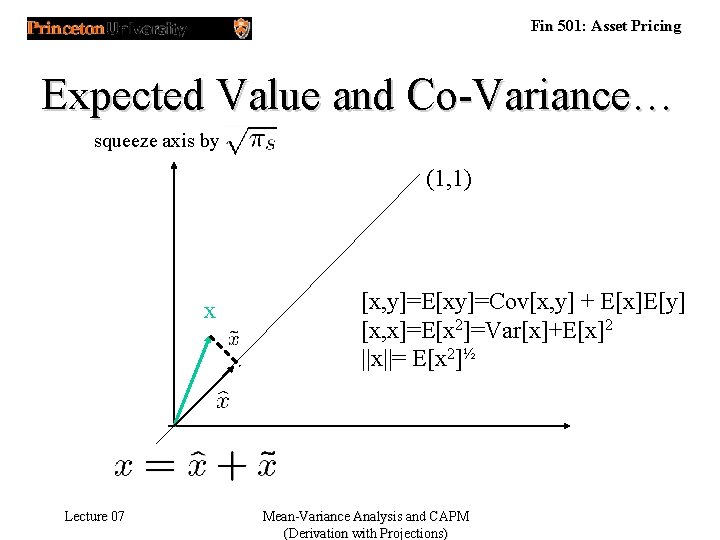
Fin 501: Asset Pricing Expected Value and Co-Variance… squeeze axis by (1, 1) x Lecture 07 [x, y]=E[xy]=Cov[x, y] + E[x]E[y] [x, x]=E[x 2]=Var[x]+E[x]2 ||x||= E[x 2]½ Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing …Expected Value and Co-Variance E[x] = [x, 1]= Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Overview • Simple CAPM with quadratic utility functions (derived from state-price beta model) • Mean-variance preferences – Portfolio Theory – CAPM (traditional derivation) • With risk-free bond • Zero-beta CAPM • CAPM (modern derivation) – Projections – Pricing Kernel and Expectation Kernel Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing New Notation (Le. Roy & Werner) • Main changes (new versus old) – gross return: – SDF: – pricing kernel: r=R m=m kq = m* – Asset span: – income/endowment: M = <X> wt = e t Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Kernel kq… • M space of feasible payoffs. • If no arbitrage and p >>0 there exists SDF m 2 RS, m >>0, such that q(z)=E(m z). • m 2 M – SDF need not be in asset span. • A pricing kernel is a kq 2 M such that for each z 2 M, q(z)=E(kq z). • (kq = m* in our old notation. ) Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing …Pricing Kernel - Examples… • Example 1: – S=3, ps=1/3 for s=1, 2, 3, – x 1=(1, 0, 0), x 2=(0, 1, 1), p=(1/3, 2/3). – Then k=(1, 1, 1) is the unique pricing kernel. • Example 2: – S=3, ps=1/3 for s=1, 2, 3, – x 1=(1, 0, 0), x 2=(0, 1, 0), p=(1/3, 2/3). – Then k=(1, 2, 0) is the unique pricing kernel. Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing …Pricing Kernel – Uniqueness • If a state price density exists, there exists a unique pricing kernel. – If dim(M) = m (markets are complete), there are exactly m equations and m unknowns – If dim(M) · m, (markets may be incomplete) For any state price density (=SDF) m and any z 2 M E[(m-kq)z]=0 m=(m-kq)+kq ) kq is the ``projection'' of m on M. • Complete markets ), kq=m (SDF=state price density) Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Expectations Kernel ke • An expectations kernel is a vector ke 2 M – Such that E(z)=E(ke z) for each z 2 M. • Example – S=3, ps=1/3, for s=1, 2, 3, x 1=(1, 0, 0), x 2=(0, 1, 0). – Then the unique $ke=(1, 1, 0). $ • • • If p >>0, there exists a unique expectations kernel. Let e=(1, …, 1) then for any z 2 M E[(e-ke)z]=0 ke is the “projection” of e on M ke = e if bond can be replicated (e. g. if markets are complete) Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

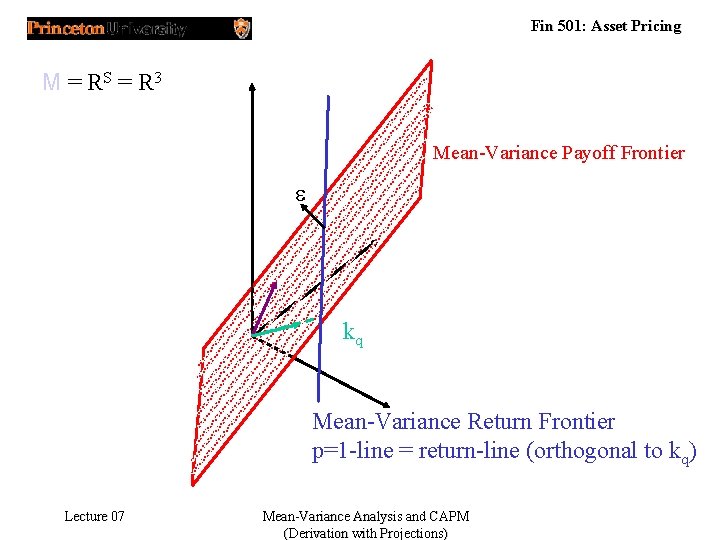
Fin 501: Asset Pricing Mean Variance Frontier • Definition 1: z 2 M is in the mean variance frontier if there exists no z’ 2 M such that E[z’]= E[z], q(z')= q(z) and var[z’] < var[z]. • Definition 2: Let E the space generated by kq and ke. • Decompose z=z. E+e, with z. E 2 E and e ? E. • Hence, E[e]= E[e ke]=0, q(e)= E[e kq]=0 Cov[e, z. E]=E[e z. E]=0, since e ? E. • var[z] = var[z. E]+var[e] (price of e is zero, but positive variance) • If z in mean variance frontier ) z 2 E. • Every z 2 E is in mean variance frontier. Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Frontier Returns… • Frontier returns are the returns of frontier payoffs with non-zero prices. • x • graphically: payoffs with price of p=1. Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing M = RS = R 3 Mean-Variance Payoff Frontier e kq Mean-Variance Return Frontier p=1 -line = return-line (orthogonal to kq) Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

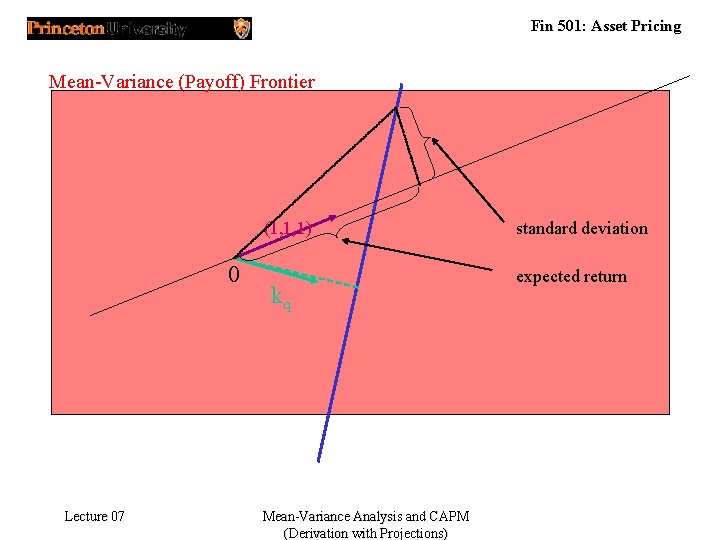
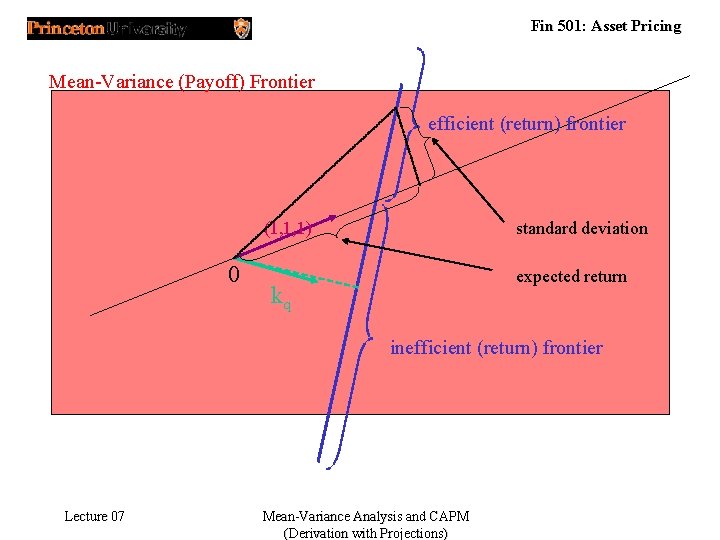
Fin 501: Asset Pricing Mean-Variance (Payoff) Frontier (1, 1, 1) 0 Lecture 07 kq Mean-Variance Analysis and CAPM (Derivation with Projections) standard deviation expected return

Fin 501: Asset Pricing Mean-Variance (Payoff) Frontier efficient (return) frontier (1, 1, 1) 0 standard deviation expected return kq inefficient (return) frontier Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

…Frontier Returns Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections) Fin 501: Asset Pricing

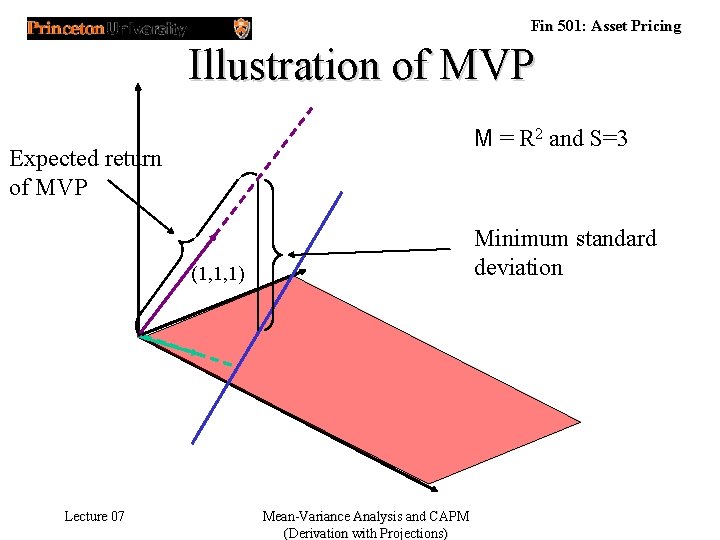
Fin 501: Asset Pricing Minimum Variance Portfolio • Take FOC w. r. t. l of • Hence, MVP has return of Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Mean-Variance Efficient Returns • Definition: A return is mean-variance efficient if there is no other return with same variance but greater expectation. • Mean variance efficient returns are frontier returns with E[rl] ¸ E[rl 0]. • If risk-free asset can be replicated – Mean variance efficient returns correspond to l · 0. – Pricing kernel (portfolio) is not mean-variance efficient, since Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Zero-Covariance Frontier Returns • Take two frontier portfolios with returns and • C • The portfolios have zero co-variance if • For all l ¹ l 0 m exists • m=0 if risk-free bond can be replicated Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Illustration of MVP M = R 2 and S=3 Expected return of MVP Minimum standard deviation (1, 1, 1) Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

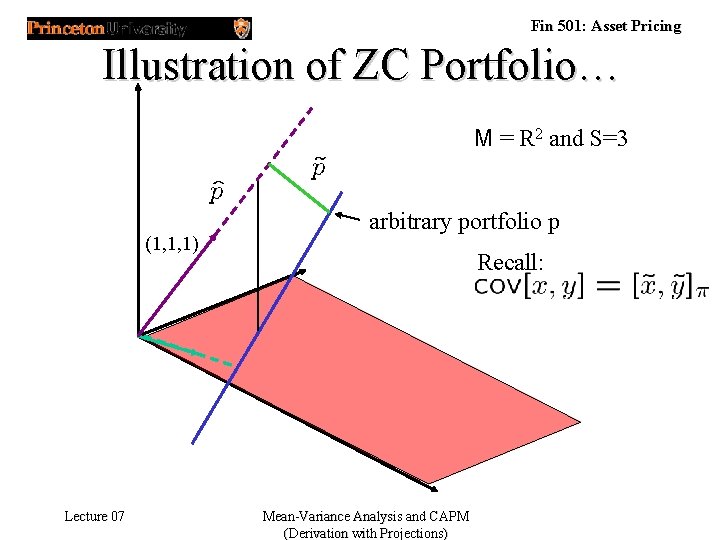
Fin 501: Asset Pricing Illustration of ZC Portfolio… M = R 2 and S=3 (1, 1, 1) Lecture 07 arbitrary portfolio p Recall: Mean-Variance Analysis and CAPM (Derivation with Projections)

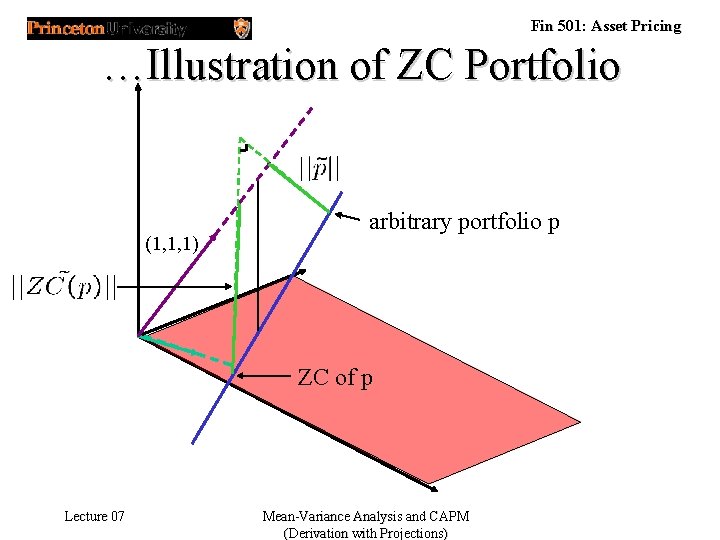
Fin 501: Asset Pricing …Illustration of ZC Portfolio (1, 1, 1) arbitrary portfolio p ZC of p Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Beta Pricing… • Frontier Returns (are on linear subspace). Hence • Consider any asset with payoff xj – It can be decomposed in xj = xj. E + ej – q(xj)=q(xj. E) and E[xj]=E[xj. E], since e ? E. – Let rj. E be the return of xj. E – Rdddf – Using above and assuming l ¹ lambda 0 and m is ZC-portfolio of l, Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing …Beta Pricing • Taking expectations and deriving covariance • _ • If risk-free asset can be replicated, beta-pricing equation simplifies to • Problem: How to identify frontier returns Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing Capital Asset Pricing Model… • CAPM = market return is frontier return – Derive conditions under which market return is frontier return – Two periods: 0, 1, – Endowment: individual wi 1 at time 1, aggregate where the orthogonal projection of on M is. – The market payoff: – Assume q(m) ¹ 0, let rm=m / q(m), and assume that rm is not the minimum variance return. Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)

Fin 501: Asset Pricing …Capital Asset Pricing Model • If rm 0 is the frontier return that has zero covariance with rm then, for every security j, • E[rj]=E[rm 0] + bj (E[rm]-E[rm 0]), with bj=cov[rj, rm] / var[rm]. • If a risk free asset exists, equation becomes, • E[rj]= rf + bj (E[rm]- rf) • N. B. first equation always hold if there are only two assets. Lecture 07 Mean-Variance Analysis and CAPM (Derivation with Projections)