FAJAR SURYANI 12 105 045 TENTANG FUNGSI 2

FAJAR SURYANI 12 105 045 TENTANG: FUNGSI( 2 SMA) MEDIA PEMBELAJARAN MATEMATIKA DOSEN: FRIDGO TASMAN M. SC

A. FUNGSI Pengertian fungsi Relasi R dari himpunan A ke himpunan B adalah pemasangan atau korespondensi antara anggota–anggota A dengan anggota–anggota B. Contoh : Lima siswa kelas XI program IPS di suatu sekolah ditanya mengenai ukuran baju seragam yang mereka kenakan dan hasilnya sebagai berikut. – Asri mengenakan baju seragam berukuran S. – Tari mengenakan baju seragam berukuran M. – Cecep mengenakan baju seragam berukuran L. – Pras mengenakan baju seragam berukuran L. – Setya mengenakan baju seragam berukuran XL. 1.

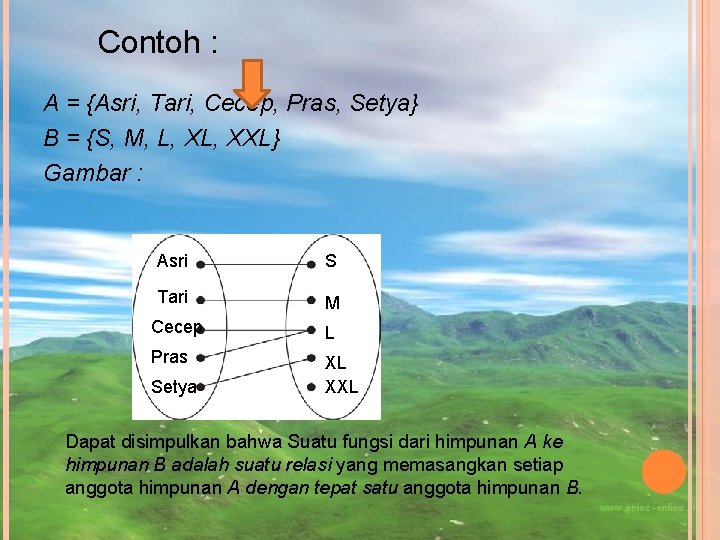
Contoh : A = {Asri, Tari, Cecep, Pras, Setya} B = {S, M, L, XXL} Gambar : Asri S Tari M Cecep L Pras XL XXL Setya Dapat disimpulkan bahwa Suatu fungsi dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap anggota himpunan A dengan tepat satu anggota himpunan B.

2. NOTASI FUNGSI f : x �� y (dibaca : f memetakan xy disebut ke y) bayangan x oleh fungsi f dan dinyatakan dengan f (x). Contoh : Tentukan bayangan 5 dan – 2 oleh f : x �� 2 x 2 + 1 dengan x �� R! Jawab: Bayangan x oleh fungsi f adalah f (x) = 2 x 2 + 1. Untuk x = 5 �� f (5) = 2. 52 + 1 = 50 + 1 = 51 Untuk x = – 2 �� f – 2) = 2. (– 2)2 + 1 = 8 + 1 = 9 Jadi, bayangan untuk fungsi f (x) = 2 x 2 + 1 adalah 51 dan 9. Bila hasilnya dinyatakan dalam pasangan berurutan, diperoleh relasi R = {(5, 51), (– 2, 9)}

3. SIFAT–SIFAT FUNGSI Fungsi satu–satu (injektif) Perhatikan diagram panah berikut ini! a 1 b 2 c 3 d 4 5 Ditentukan fungsi f : A B yang didefinisikan sebagai diagram panah di samping. Dari diagram dapat terlihat bahwa setiap anggota himpunan A dipasangkan tepat satu anggota himpunan B yang berbeda. Fungsi yang seperti ini disebut fungsi satu–satu.

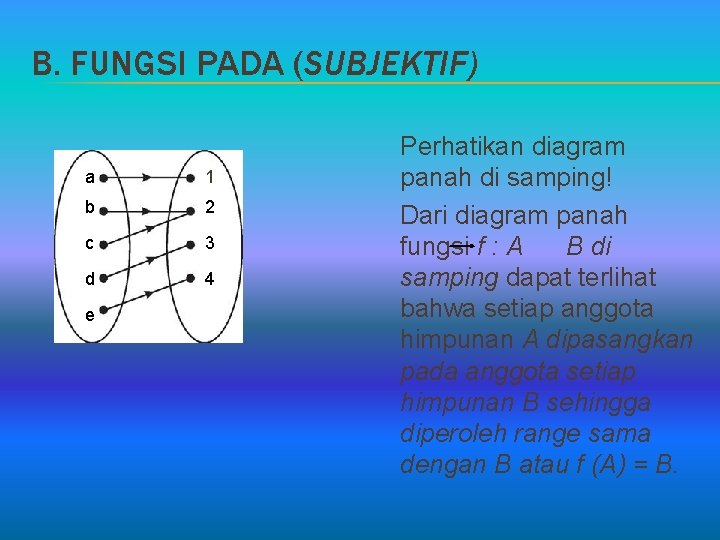
B. FUNGSI PADA (SUBJEKTIF) a 1 b 2 c 3 d 4 e Perhatikan diagram panah di samping! Dari diagram panah fungsi f : A B di samping dapat terlihat bahwa setiap anggota himpunan A dipasangkan pada anggota setiap himpunan B sehingga diperoleh range sama dengan B atau f (A) = B.

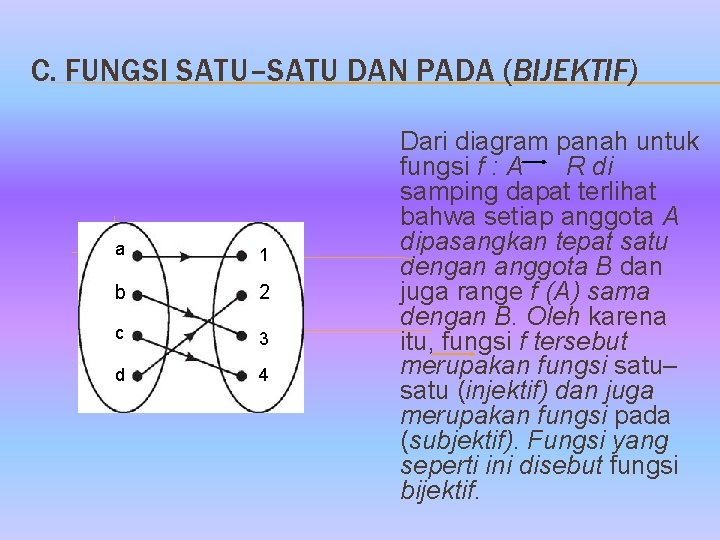
C. FUNGSI SATU–SATU DAN PADA (BIJEKTIF) a 1 b 2 c 3 d 4 Dari diagram panah untuk fungsi f : A R di samping dapat terlihat bahwa setiap anggota A dipasangkan tepat satu dengan anggota B dan juga range f (A) sama dengan B. Oleh karena itu, fungsi f tersebut merupakan fungsi satu– satu (injektif) dan juga merupakan fungsi pada (subjektif). Fungsi yang seperti ini disebut fungsi bijektif.

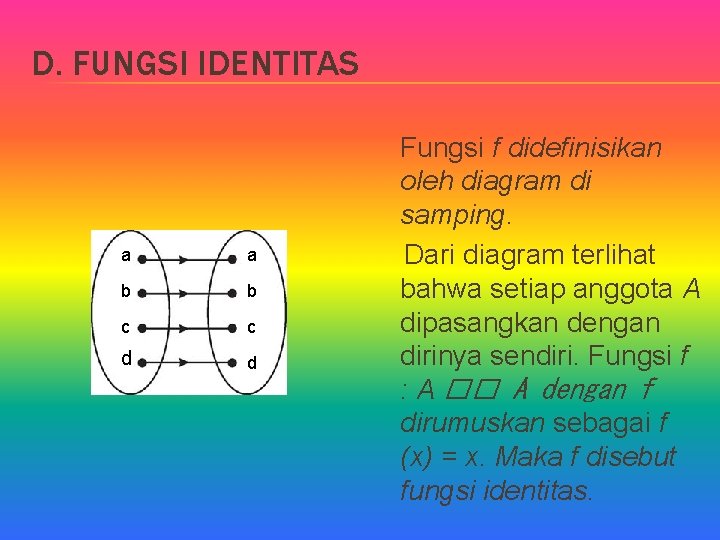
D. FUNGSI IDENTITAS a a b b c c d d Fungsi f didefinisikan oleh diagram di samping. Dari diagram terlihat bahwa setiap anggota A dipasangkan dengan dirinya sendiri. Fungsi f : A �� A dengan f dirumuskan sebagai f (x) = x. Maka f disebut fungsi identitas.

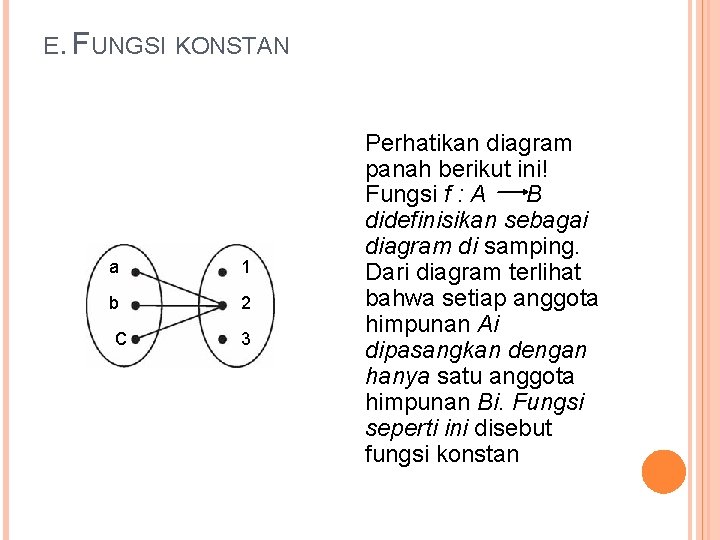
E. FUNGSI KONSTAN a 1 b 2 c 3 Perhatikan diagram panah berikut ini! Fungsi f : A B didefinisikan sebagai diagram di samping. Dari diagram terlihat bahwa setiap anggota himpunan Ai dipasangkan dengan hanya satu anggota himpunan Bi. Fungsi seperti ini disebut fungsi konstan

B. FUNGSI KOMPOSISI 1. Pengertian Fungsi Komposisi Jika f : A B dan fungsi g : B C, maka fungsi F yang memetakan A C melalui hubungan dua fungsi f dan g, dapat dinyatakan sebagai fungsi komposisi. Secara matematis ditulis: F : A C atau F : x g (f (x)) dengan rumus F (x) = g (f (x)). Dengan demikian, dapat disimpulkan bahwa: Fungsi f (x) = g (x) adalah komposisi fungsi f dan g, sehingga f (x) disebut fungsi komposisi. F: x (gof) (x) = g (f (x))

2. FUNGSI KOMPOSISI BILANGAN REAL Misalkan f : R R dan g : R R adalah dua fungsi, maka dapat didefinisikan F : gof dan juga F = fog. Contoh : 1. Diketahui fungsi f : R R dan g : R R ditentukan oleh f (x) = 3 x + 2 dan g (x) = x 2 + 2. Tentukan: a. (gof) (1) b. (fog) (1) c. Bandingkan hasil (a) dan (b), berilah kesimpulan. Jawab: f (x) = 3 x + 2 dan g (x) = x 2 + 2 a. (fog) (1) = g (f (1)) = 9 (3. 1 + 2) = 9 (5) = 52 + 2 = 27 b. (fog) (1) = f (g (1)) = f (12 + 2) = f (3) = 3. 3 + 2 = 11 c. Hasil fungsi gof dan fog tidak sama. Jadi, dapat disimpulkan bahwa fungsi komposisi tidak komutatif.

3. SIFAT FUNGSI KOMPOSISI Fungsi komposisi tidak memiliki sifat komutatif, yaitu (fog) (gof). Contoh soal : Diketahui f : R R, g : R R, dan h : R R ditentukan oleh rumus f (x) = 2 x + 4, g (x) = 3 x, dan h (x) = x 2 + 1. Tentukan: a. ((fog)oh) (x); b. (fo (goh)) (x)! c. Bandingkan hasil a dan b. Apa yang dapat Anda simpulkan?

LANJUTAN : Jawab: a. (fog) (x) = f (g (x)) = f (3 x) = 2 (3 x) + 4 = 6 x + 4 ((fog)oh) (x) = (fog) (h(x)) = (fog) (x 2 + 1) = 6 (x 2 + 1) + 4 = 6 x 2 + 6 + 4 = 6 x 2 + 10 Jadi, ((fog)oh) (x) = 6 x 2 + 10 b. (goh) (x) = g (h (x)) = g (x 2 + 1) = 3 x 2 + 3 (fo(goh)) (x) = f ((goh) (x)) = f (3 x 2 + 3) = 2 (3 x 2 + 3) + 4 = 6 x 2 + 6 + 4 = 6 x 2 + 10 Jadi, (fo(goh)) (x) = 6 x 2 + 10

LANJUTAN : c. Hasil dari (fog)oh dan fo(goh) adalah sama, maka dapat disimpulkan bahwa: Fungsi komposisi memiliki sifat asosiatif, yaitu (fog)oh = fo(goh) Apabila pada contoh di atas diketahui fungsi identitas I pada R yang ditentukan oleh rumus I (x) = x maka nilai Iof dan fo. I adalah: (Iof) (x) = I (f (x)) = I (2 x + 4) = 2 x + 4 (fo. I) (x) = f (I (x)) = f (x) = 2 x + 4 Hasil dari Iof dan fo. I adalah sama, sehingga dapat disimpulkan bahwa: Ada fungsi identitas, yaitu I (x) = x, artinya untuk setiap f akan berlaku fo. I = Iof = f.

Thanks for you attention