FA Algorithms Finite Automata Part Three Kleene Star

FA Algorithms Finite Automata Part Three

Kleene Star L={a} L* = { e, a, aaa, … } L = { a, bb } L* = { e, a, bba, aaa, bbbb, bbabbaaa…}

Got it? given L = { ab, aba } Which of the following words are accepted by L*? Ø aaaa Ø ababa Ø abaab Ø ababaab

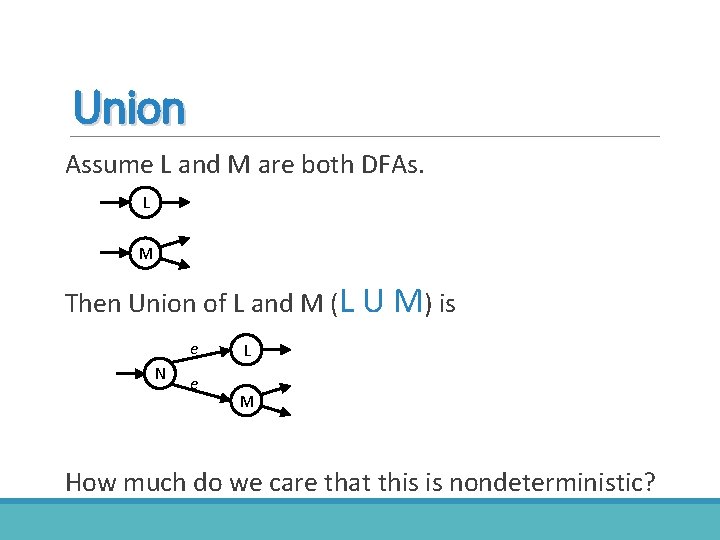
Union Assume L and M are both DFAs. L M Then Union of L and M (L U M) is e N e L M How much do we care that this is nondeterministic?

Complement of L is written ∑* - L 1. Convert the FA to a DFA. 2. Flip favorable states to unfavorable and vice versa.

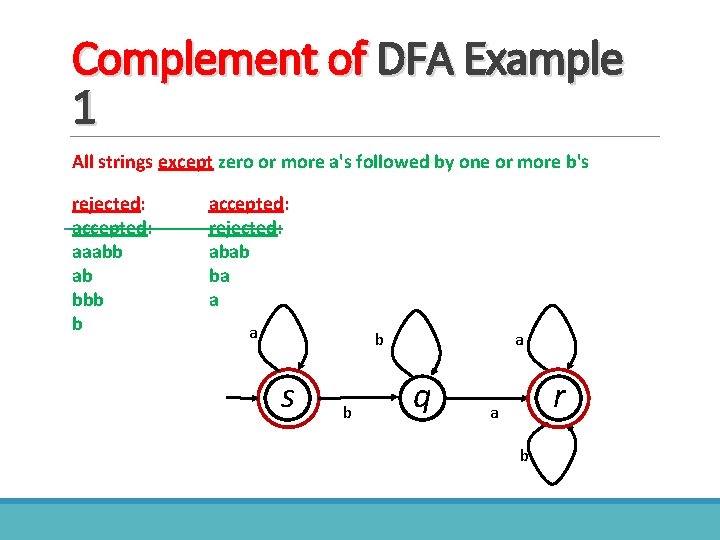
Complement of DFA Example 1 All strings except zero or more a's followed by one or more b's rejected: accepted: aaabb ab bbb b accepted: rejected: abab ba a a b s b a q r a b

Intersection L ∩ M = complement of ( ∑* - L ) U ( ∑* - M ) 1. Build the complement of L and complement of M 2. Build union of those complements. 3. Build the complement of that union.

Difference L - M = L ∩ ( ∑* - M ) 1. Build complement of M 2. Build intersection of that FA and L.

Concatenation of L and M is written LM. 1. Add an arrow labeled e from every favorable state of L to the initial state of M.

Membership If A is an FA, and L(A) is the language (set of words) accepted by A. Then how do we determine if word w is a member of L(A)? w ∈ L(A) Just run w through the FA.

Empty Language How do we determine if L(A) is empty? Are there any paths from the initial state to any favorable state? If all favorable state are unreachable then L(A) is empty.

Subset of a Language L(A) ⊆ L(B) 1. Build language C where L(C) = L(A) - L(B) 2. If L(C) is empty, then L(A) ⊆ L(B)

Equality Is L(A) = L(B) ? Language A and B are equal if L(A) ⊆ L(B) and L(B) ⊆ L(A)

State Minimization Why do we care about the number of states in a Finite Automata?

State Minimization Step 1 : Remove unreachable states. Step 2 : Remove equivalent states. Sometimes it is obvious looking at the state table that two states have the same outputs. See previously used example of converting an NFA to a DFA.

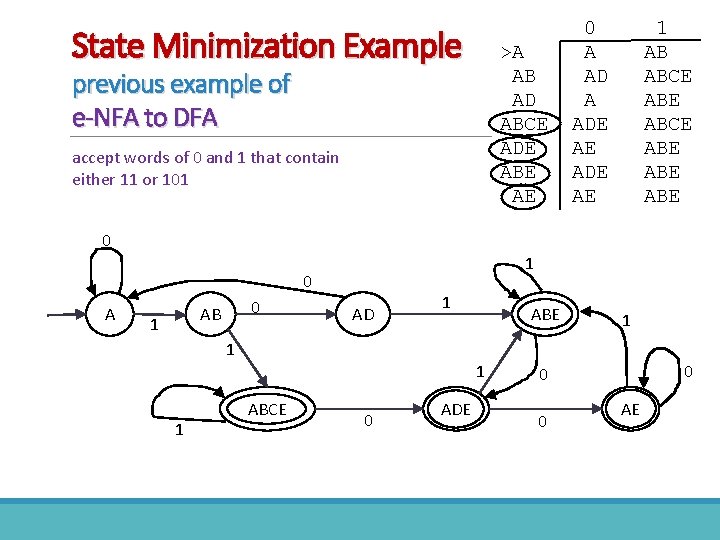
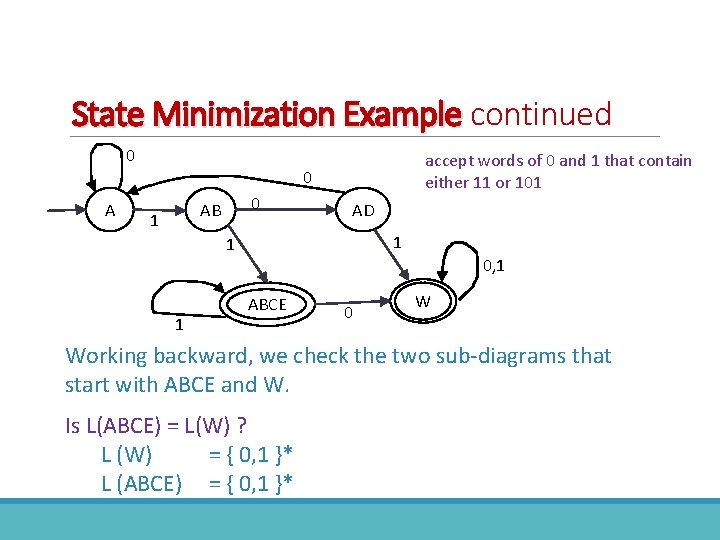
State Minimization Example >A AB AD ABCE ADE ABE AE previous example of e-NFA to DFA accept words of 0 and 1 that contain either 11 or 101 0 A ADE AE 1 AB ABCE ABE ABE 0 1 0 AB 1 AD 1 ABE 1 1 ABCE 0 ADE 0 0 0 AE

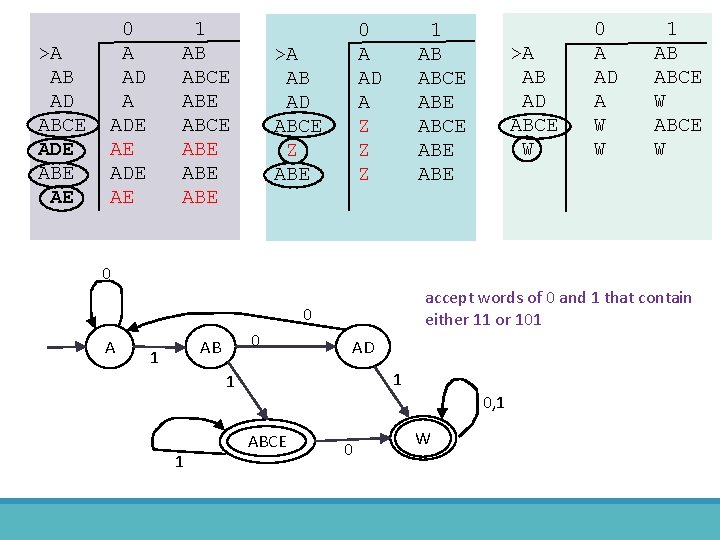
>A AB AD ABCE ADE ABE AE 0 A ADE AE 1 AB ABCE ABE ABE 0 A AD A Z Z Z >A AB AD ABCE Z ABE 1 AB ABCE ABE ABE >A AB AD ABCE W 0 A AD A W W 1 AB ABCE W 0 accept words of 0 and 1 that contain either 11 or 101 0 AB 1 AD 1 1 1 0, 1 ABCE 0 W

FA State Minimization Algorithm Working backward from each favorable state to determine if two sub-FAs are equivalent: make both states start states determine accepted languages in other words, is L(A) = L(B) ?

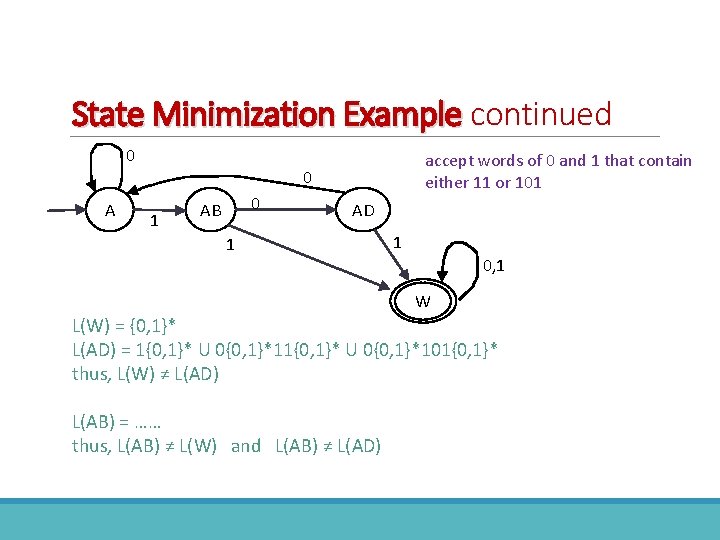
State Minimization Example continued 0 A accept words of 0 and 1 that contain either 11 or 101 0 0 AB 1 AD 1 1 1 0, 1 ABCE 0 W Working backward, we check the two sub-diagrams that start with ABCE and W. Is L(ABCE) = L(W) ? L (W) = { 0, 1 }* L (ABCE) = { 0, 1 }*

State Minimization Example continued 0 A accept words of 0 and 1 that contain either 11 or 101 0 AB AD 1 1 0, 1 W L(W) = {0, 1}* L(AD) = 1{0, 1}* U 0{0, 1}*101{0, 1}* thus, L(W) ≠ L(AD) L(AB) = …… thus, L(AB) ≠ L(W) and L(AB) ≠ L(AD)