Lecture 10 Kleenes Theorem Kleenes Theorem Part III

Lecture # 10 (Kleene’s Theorem)

Kleene’s Theorem Part III n n n Statement: If the language can be expressed by a RE then there exists an FA accepting the language. (A) As the regular expression is obtained applying addition, concatenation and closure on the letters of an alphabet and the Null string, so while building the RE, sometimes, the corresponding FA may be built easily, as shown in the following examples

Example n n Consider the language, defined over Σ={a, b}, consisting of only b, then this language may be accepted by the following FA which shows that this FA helps in building an FA accepting only one letter

Example n Consider the language, defined over Σ={a, b}, consisting of only Λ , then this language may be accepted by the following FA

Kleene’s Theorem Part III Continued … n (B) As, if r 1 and r 2 are regular expressions then their sum, concatenation and closure also regular expressions, so an FA can be built for any regular expression if the methods can be developed for building the FAs corresponding to the sum, concatenation and closure of the regular expressions along with their FAs. These three methods are explained in the following discussions

Kleene’s Theorem Part III Continued … n Method 1 (Union of two FAs): Using the FAs corresponding to r 1 and r 2 an FA can be built, corresponding to r 1 + r 2. This method can be developed considering the following examples

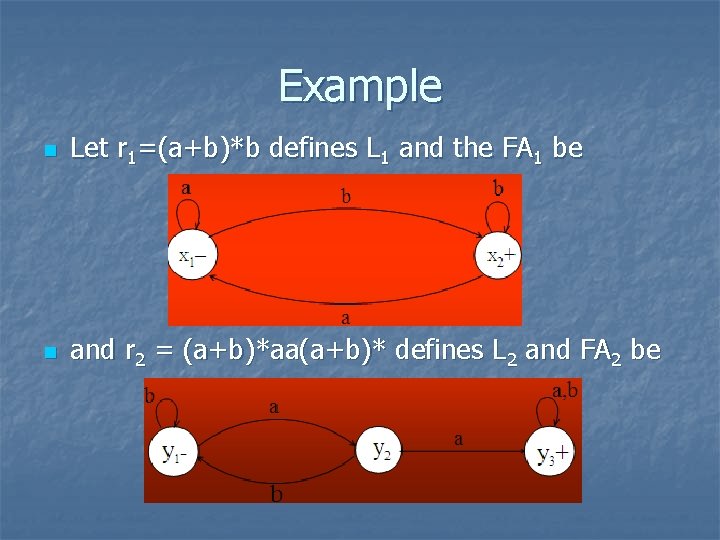
Example n Let r 1=(a+b)*b defines L 1 and the FA 1 be n and r 2 = (a+b)*aa(a+b)* defines L 2 and FA 2 be

Sum of two FAs Continued … n n Let FA 3 be an FA corresponding to r 1+ r 2, then the initial state of FA 3 must correspond to the initial state of FA 1 or the initial state of FA 2. Since the language corresponding to r 1+ r 2 is the union of corresponding languages L 1 and L 2, consists of the strings belonging to L 1 or L 2 or both, therefore a final state of FA 3 must correspond to a final state of FA 1 or FA 2 or both.

Sum of two FAs Continued … n Since, in general, FA 3 will be different from both FA 1 and FA 2, so the labels of the states of FA 3 may be supposed to be z 1, z 2, z 3, …, where z 1 is supposed to be the initial state. Since z 1 corresponds to the states x 1 or y 1, so there will be two transitions separately for each letter read at z 1. It will give two possibilities of states either z 1 or different from z 1. This process may be expressed in the following transition table for all possible states of FA 3.

Example continued … New states after reading Old states z 1– € (x 1, y 1) a b (x 1, y 2) € z 2 (x 2, y 1) € z 3

Example continued … New states after reading Old states a b z 1– € (x 1, y 1) (x 1, y 2) € z 2 (x 2, y 1) € z 3 z 2 € (x 1, y 2) (x 1, y 3) € z 4 (x 2, y 1) € z 3 + € (x 2, y 1) (x 1, y 2) € z 2 (x 2, y 1) € z 3 z 4 + € (x 1, y 3) € z 4 (x 2, y 3) € z 5 + € (x 2, y 3) (x 1, y 3) € z 4 (x 2, y 3) € z 5

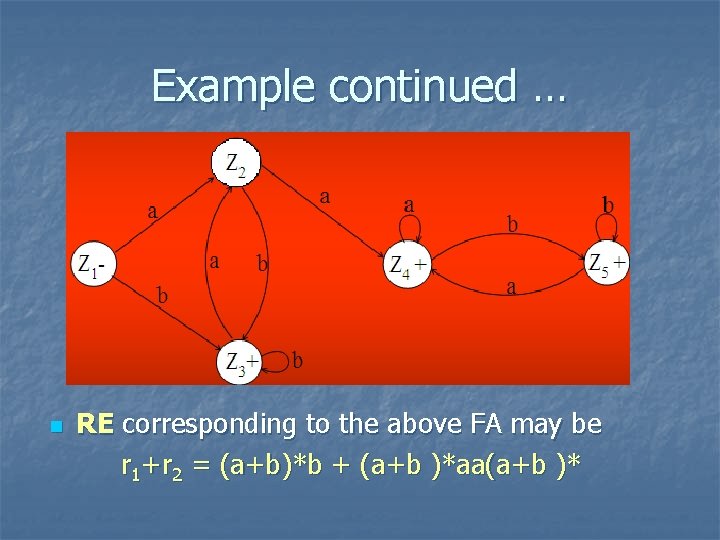
Example continued … n RE corresponding to the above FA may be r 1+r 2 = (a+b)*b + (a+b )*aa(a+b )*

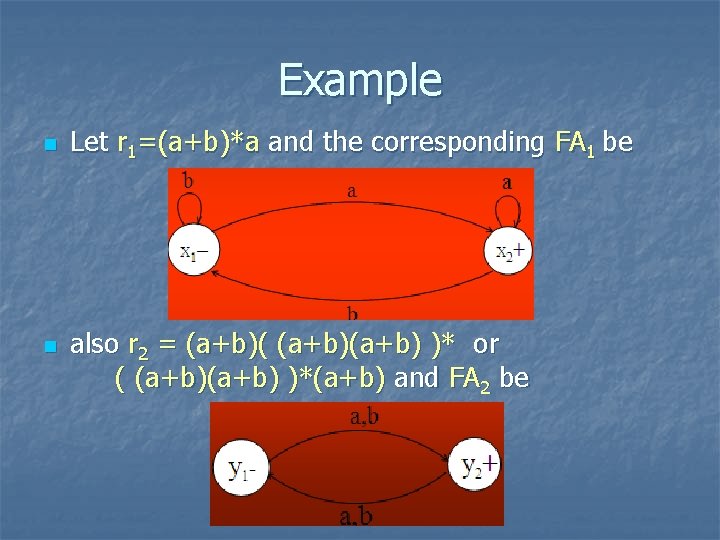
Example n n Let r 1=(a+b)*a and the corresponding FA 1 be also r 2 = (a+b)(a+b) )* or ( (a+b) )*(a+b) and FA 2 be

TASK n Generate Union of FAs corresponding to r 1 and r 2 i. e. r 1+ r 2

Assignment No 1 n n n Input FA 1 and FA 2 representing r 1 and r 2 respectively. Generate a final automata FA 3 representing the Union of FA 1 and FA 2 corresponding to r 1+ r 2. Based on the algorithm studied of Union of two FAs. Due: 26 th Dec, 2013

Kleene’s Theorem Part III Continued … n Method 2 (Concatenation of two FAs): Using the FAs corresponding to r 1 and r 2 , an FA can be built, corresponding to r 1 r 2. This method can be developed considering the following examples

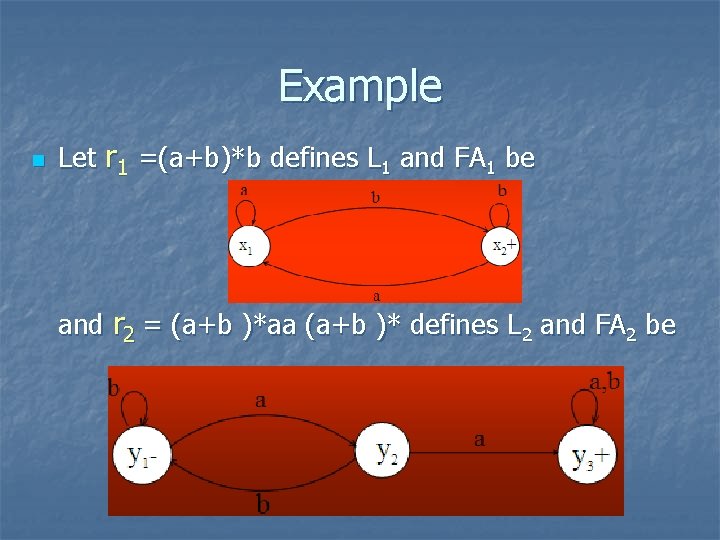
Example n Let r 1 =(a+b)*b defines L 1 and FA 1 be and r 2 = (a+b )*aa (a+b )* defines L 2 and FA 2 be

Concatenation of two FAs Continued … n Let FA 3 be an FA corresponding to r 1 r 2 , then the initial state of FA 3 must correspond to the initial state of FA 1 and the final state of FA 3 must correspond to the final state of FA 2. Since the language corresponding to r 1 r 2 is the concatenation of corresponding languages L 1 and L 2 , consists of the strings obtained, concatenating the strings of L 1 to those of L 2 , therefore the moment a final state of first FA is entered, the possibility of the initial state of second FA will be included as well.

Concatenation of two FAs Continued … n Since, in general, FA 3 will be different from both FA 1 and FA 2 , so the labels of the states of FA 3 may be supposed to be z 1, z 2, z 3, …, where z 1 stands for the initial state. Since z 1 corresponds to the states x 1 , so there will be two transitions separately for each letter read at z 1. It will give two possibilities of states which correspond to either z 1 or different from z 1. This process may be expressed in the following transition table for all possible states of FA 3

Example continued … New states after reading Old states z 1 – € x 1 a b x 1 € z 1 (x 2, y 1) € z 2

Example continued … New states after reading Old states a b z 1 – € x 1 € z 1 (x 2, y 1) € z 2 € (x 2, y 1) (x 1, y 2) € z 3 (x 2, y 1) € z 2 z 3 € (x 1, y 2) (x 1, y 3) € z 4 (x 2, y 1) € z 2 z 4 + € ( x 1 , y 3 ) (x 1, y 3) € z 4 ( x 2 , y 1 , y 3 ) € z 5 + € (x 2, y 1, y 3) (x 1, y 2, y 3) € z 6 (x 2, y 1, y 3) € z 5 z 6 + € (x 1, y 2, y 3) (x 1, y 3) € z 4 ( x 2 , y 1 , y 3 ) € z 5

Example continued …

Example n Let r 1 =((a+b))* , the corresponding FA 1 be also r 2 = (a+b)(a+b))* or ((a+b))*(a+b) and FA 2 be

TASK n Generate the FA representing r 1 r 2 using Concatenation Algorithm