DR Torng Closure Properties for CFLs Kleene Closure

DR. Torng • Closure Properties for CFL’s – Kleene Closure – Union – Concatenation • CFL’s versus regular languages – regular languages subset of CFL 1

Closure Properties for CFL’s Kleene Closure 2

CFL closed under Kleene Closure • Let L be an arbitrary CFL • Let G 1 be a CFG s. t. L(G 1) = L – G 1 exists by definition of L 1 in CFL • • Construct CFG G 2 from CFG G 1 Argue L(G 2) = L* There exists CFG G 2 s. t. L(G 2) = L* L* is a CFL 3

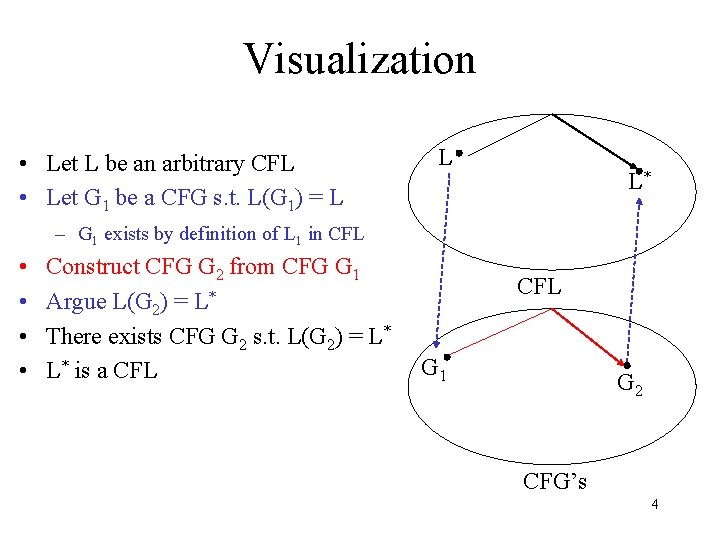
Visualization • Let L be an arbitrary CFL • Let G 1 be a CFG s. t. L(G 1) = L L L* – G 1 exists by definition of L 1 in CFL • • Construct CFG G 2 from CFG G 1 Argue L(G 2) = L* There exists CFG G 2 s. t. L(G 2) = L* L* is a CFL G 1 G 2 CFG’s 4

Algorithm Specification • Input – CFG G 1 • Output – CFG G 2 such that L(G 2) = CFG G 1 A CFG G 2 5

Construction • Input – CFG G 1 = (V 1, S, S 1, P 1) • Output – CFG G 2 = (V 2, S, S 2, P 2) • V 2 = V 1 union {T} – T is a new symbol not in V 1 or S • S 2 = T • P 2 = P 1 union ? ? 6

Closure Properties for CFL’s Kleene Closure Examples 7

Example 1 • Input grammar: – – V = {S} S = {a, b} S=S P: V 2 = V 1 union {T} T is a new symbol not in V 1 or S S 2 = T P 2 = P 1 union {T → ST | l} • Output grammar – – V= S = {a, b} Start symbol is P: S → aa | ab | ba | bb 8

Example 2 • Input grammar: – – V = {S, T} S = {a, b} Start symbol is T P: V 2 = V 1 union {T} T is a new symbol not in V 1 or S S 2 = T P 2 = P 1 union {T → ST | l} • Output grammar – – V= S = {a, b} Start symbol is P: T → ST | l S → aa | ab | ba | bb 9

Construction for Set Union • Input – CFG G 1 = (V 1, S, S 1, P 1) – CFG G 2 = (V 2, S, S 2, P 2) • Output – CFG G 3 = (V 3, S, S 3, P 3) • V 3 = V 1 union V 2 union {T} – Variable renaming to insure no names shared between V 1 and V 2 – T is a new symbol not in V 1 or V 2 or S • S 3 = T • P 3 = 10

Construction for Set Concatenation • Input – CFG G 1 = (V 1, S, S 1, P 1) – CFG G 2 = (V 2, S, S 2, P 2) • Output – CFG G 3 = (V 3, S, S 3, P 3) • V 3 = V 1 union V 2 union {T} – Variable renaming to insure no names shared between V 1 and V 2 – T is a new symbol not in V 1 or V 2 or S • S 3 = T • P 3 = 11

CFL’s and regular languages 12

CFL Closure Properties • What have we just proven – CFL’s are closed under Kleene closure – CFL’s are closed under set union – CFL’s are closed under set concatenation • What can we conclude from these 3 results? – It follows that regular languages are a subset of CFL’s 13

Regular languages subset of CFL • Similar to reg-exp to NFA-λ construction from module 22 – Base Case: • {}, {l}, {a}, {b} are regular languages over {a, b} • P={}, P={S → l}, P={S → a}, P={S → b} – Inductive Case: • If L 1 and L 2 are regular languages, then L 1*, L 1 L 2, L 1 union L 2 are regular languages • Use previous constructions to see that these resulting languages are also context-free 14

Other CFL Closure Properties • We will show that CFL’s are NOT closed under many other set operations • Examples include – set complement – set intersection – set difference 15

Language class hierarchy ? H H Equal REG CFL REC RE All languages over alphabet S 16

Nested language examples • Prove the following languages are CFLs – {anbncmdm | m, n ≥ 0} – {anbmcmdn | m, n ≥ 0} – {am+nbmcn | m, n ≥ 0} – What happens if we change bounds above to 1 instead of 0? 17