Finite State Automata Finite State Automata A very

Finite State Automata

Finite State Automata • A very simple and intuitive formalism suitable for certain tasks • A bit like a flow chart, but can be used for both recognition and generation • “Transition network” • Unique start point • Series of states linked by transitions • Transitions represent input to be accounted for, or output to be generated • Legal exit point(s) explicitly identified

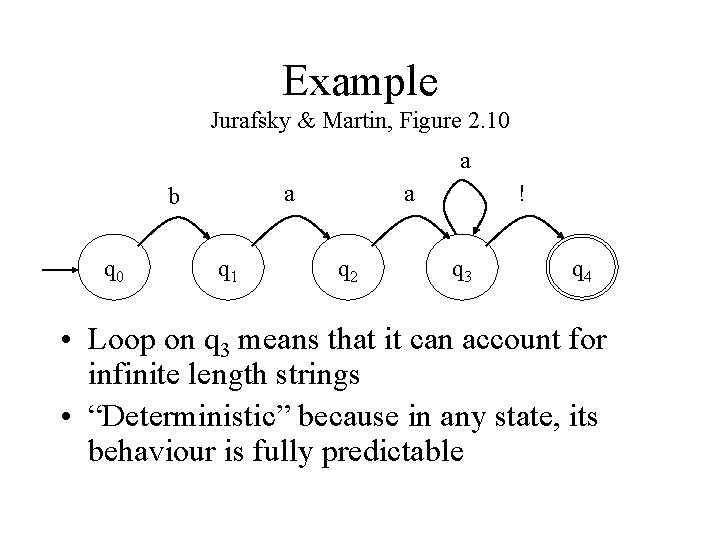
Example Jurafsky & Martin, Figure 2. 10 a a b q 0 q 1 a q 2 ! q 3 q 4 • Loop on q 3 means that it can account for infinite length strings • “Deterministic” because in any state, its behaviour is fully predictable

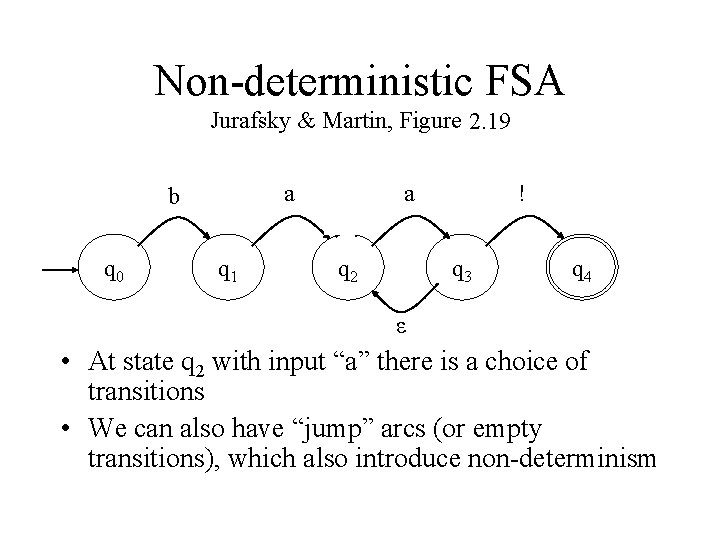
Non deterministic FSA Jurafsky & Martin, Figure 2. 18 2. 19 a a b q 0 q 1 a q 2 ! q 3 q 4 ε • At state q 2 with input “a” there is a choice of transitions • We can also have “jump” arcs (or empty transitions), which also introduce non determinism

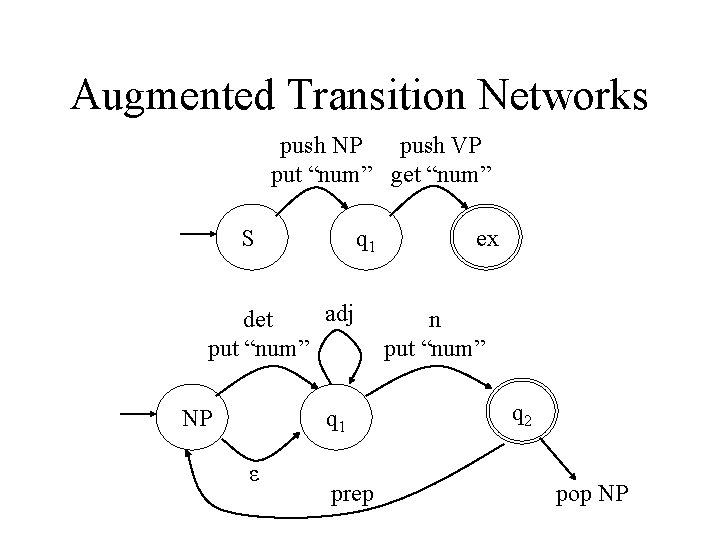
Augmented Transition Networks • ATNs were used for parsing in the 60 s and 70 s • For parsing, you need to pass constraints (e. g. for agreement) as well as account for input: the Transition Networks were “augmented” by having a “register” into/from which such information could be put/taken. • It’s easy to write recognizers, but computing structure is difficult • ATNs quickly become very complex; one solution isto have a “cascade” of ATNs, where transitions can call other networks

Augmented Transition Networks push NP push VP put “num” get “num” S q 1 adj det put “num” NP q 1 ε prep ex n put “num” q 2 pop NP

Exercises a a b q 0 [0, b, 1] q 1 a q 2 [1, a, 2] ! q 3 q 4 [2, a, 3] [3, !, end] fsa([[0, b, 1], [1, a, 2], [2, a, 3], [3, !, end]]).

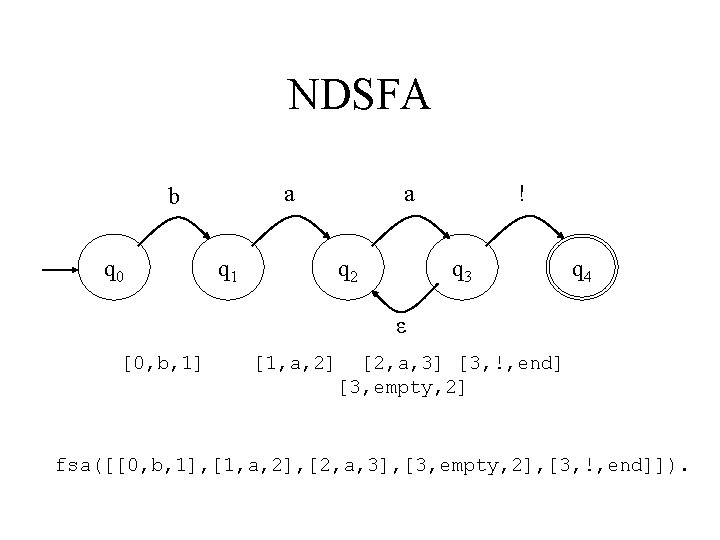
NDSFA a b q 0 q 1 a q 2 ! q 3 q 4 ε [0, b, 1] [1, a, 2] [2, a, 3] [3, !, end] [3, empty, 2] fsa([[0, b, 1], [1, a, 2], [2, a, 3], [3, empty, 2], [3, !, end]]).

FSA and NDFSA programs First load (consult) the file, eg 219. pl | ? - help. Options are as follows run - a simple recognizer; on prompt type in string with space between each element, ending in. or ! or ? run(v) - verbose recognizer gives trace of transitions gen(X) - generate text; will interact at choice points rec(X, quiet) - to generate text deterministically. Type ; to get other grammatical sequences | ? - run. Enter your string: b a a ! yes

FSA and NDFSA programs | ? - run(v). Enter your string: b a a ! 0 -b-1 1 -a-2 2 -a-3 3 -skip-2 3 -!-end yes

FSA and NDFSA programs | ? - gen(X). Choice at state 3. Choose state from (1) [!, end] (2) [empty, 2] Select choice number: 2. Choice at state 3. Choose state from (1) [!, end] (2) [empty, 2] Select choice number: 1. X = [b, a, a, !] ? yes

FSA and NDFSA programs | ? - rec(X, quiet). X = [b, a, a] ? ; X = [b, a, a, a] ? yes

FSAs and regular expressions • FSAs have a close relationship with “regular expressions”, a formalism for expressing strings, mainly used for searching texts, or stipulating patterns of strings • Regular expressions are defined by combinations of literal characters and special operators

Regular expressions Character [ ] [^ ] ? * +. ^, $ | ( ) etc. Meaning alternatives range not optionality zero or more one or more any character start, end of line not special character alternate strings substring Examples /[aeiou]/, /m[ae]n/ /[a z]/ /[^pbm]/, /[^ox]s/ /Kath? mandu/ /baa*!/ /ba+!/ /cat. [aeiou]/ . ? ^ /cat|dog/ /cit(y|ies)/

Regular expressions • A regular expression can be mapped onto an FSA • Can be a good way of handling morphology • Especially in connection with Finite State Transducers

Finite State Transducers • A “transducer” defines a relationship (a mapping) between two things • Typically used for “two level morphology”, but can be used for other things • Like an FSA, but each state transition stipulates a pair of symbols, and thus a mapping

Finite State Transducers • Three functions: – Recognizer (verification): takes a pair of strings and verifies if the FST is able to map them onto each other – Generator (synthesis): can generate a legal pair of strings – Translator (transduction): given one string, can generate the corresponding string

Some conventions • Transitions are marked by “: ” • A non changing transition “x: x” can be shown simply as “x” • Wild cards are shown as “@” • Empty string shown as “ε”

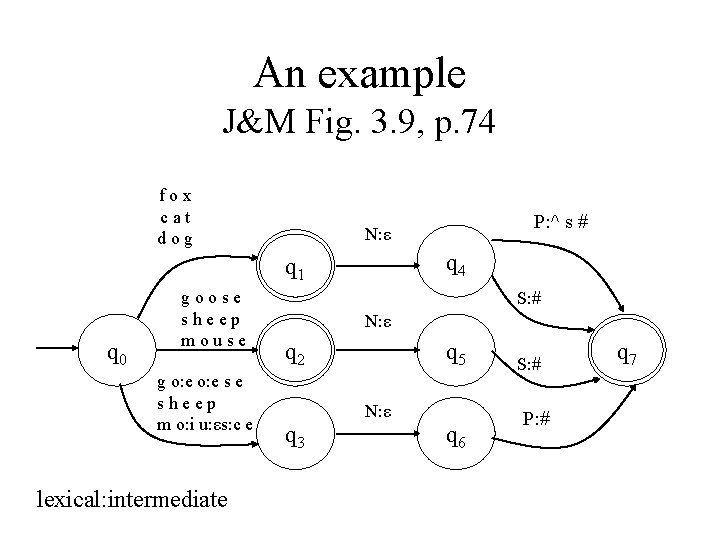
An example J&M Fig. 3. 9, p. 74 fox cat dog q 4 q 1 q 0 goose sheep mouse g o: e s e sheep m o: i u: εs: c e lexical: intermediate P: ^ s # N: ε S: # N: ε q 2 q 5 N: ε q 3 q 6 S: # P: # q 7

[0] f: f o: o x: x [1] N: ε [4] P: ^ s: s #: # [7] [0] f: f o: o x: x [1] N: ε [4] S: # [7] [0] c: c a: a t: t [1] N: ε [4] P: ^ s: s #: # [7] [0] s: s h: h e: e p: p [2] N: ε [5] S: # [7] [0] g: g o: o s: s e: e [2] N: ε [5] P: # [7] fox cat dog fox. NPs#: fox^s# fox. NS: fox# cat. NPs#: cat^s# sheep. NS: sheep# goose. NP: geese# q 4 q 1 q 0 goose sheep mouse g o: e s e sheep m o: i u: εs: c e P: ^ s # N: ε S: # N: ε q 2 q 5 N: ε q 3 q 6 S: # P: # q 7

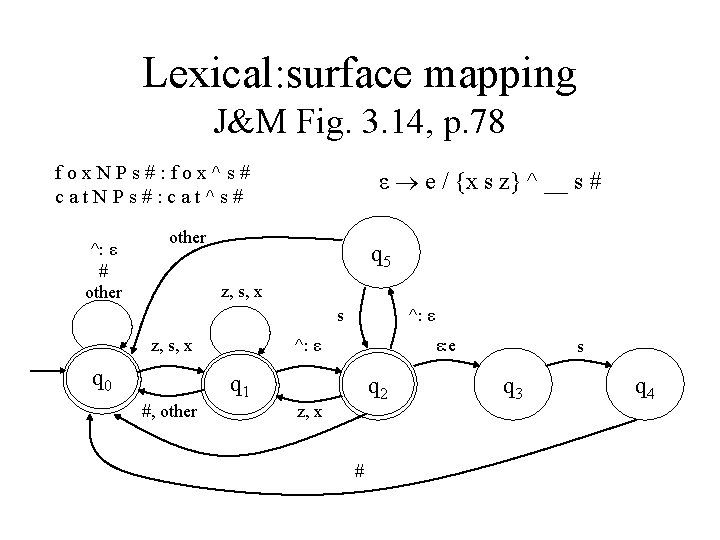
Lexical: surface mapping J&M Fig. 3. 14, p. 78 fox. NPs#: fox^s# cat. NPs#: cat^s# ^: ε # other ε e / {x s z} ^ __ s # other q 5 z, s, x s z, s, x q 0 ^: ε ε: e q 1 #, other q 2 z, x # s q 3 q 4

[0] f: f [0] o: o [0] x: x [1] ^: ε [2] ε: e [3] s: s [4] #: # [0] c: c [0] a: a [0] t: t [0] ^: ε [0] s: s [0] #: # [0] fox^s#foxes# cat^s#: cat^s# ^: ε # other q 5 z, s, x s z, s, x q 0 ^: ε ε: e q 1 #, other q 2 z, x # s q 3 q 4

FST • Can be generated automatically • Therefore, slightly different formalism

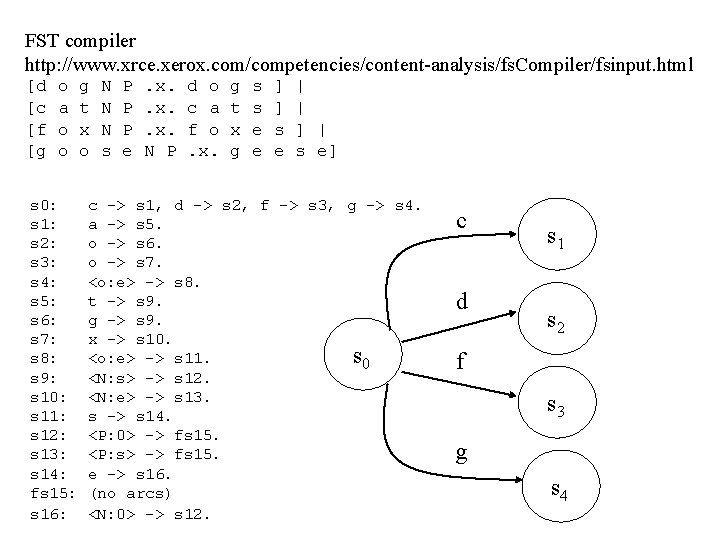
FST compiler http: //www. xrce. xerox. com/competencies/content analysis/fs. Compiler/fsinput. html [d [c [f [g o a o o s 0: s 1: s 2: s 3: s 4: s 5: s 6: s 7: s 8: s 9: s 10: s 11: s 12: s 13: s 14: fs 15: s 16: g t x o N N N s P P P e . x. N P d o c a f o. x. g t x g s s e e ] ] s e | | ] | s e] c -> s 1, d -> s 2, f -> s 3, g -> s 4. a -> s 5. o -> s 6. o -> s 7. <o: e> -> s 8. t -> s 9. g -> s 9. x -> s 10. s 0 <o: e> -> s 11. <N: s> -> s 12. <N: e> -> s 13. s -> s 14. <P: 0> -> fs 15. <P: s> -> fs 15. e -> s 16. (no arcs) <N: 0> -> s 12. c d s 1 s 2 f s 3 g s 4

s 0: s 1: s 2: s 3: s 4: s 5: s 6: s 7: s 8: s 9: s 10: s 11: s 12: s 13: s 14: fs 15: s 16: c -> s 1, d -> s 2, f -> s 3, g -> s 4. a -> s 5. fst([ o -> s 6. o -> s 7. [s 0, [c, s 1], [d, s 2], [f, s 3], <o: e> -> s 8. [g, s 4]], t -> s 9. [s 1, [a, s 5]], g -> s 9. [s 2, [o, s 6]], x -> s 10. [s 3, [o, s 7]], <o: e> -> s 11. [s 4, [[o, e], s 8]], <N: s> -> s 12. [s 5, [t, s 9]], <N: e> -> s 13. [s 6, [g, s 9]], s -> s 14. <P: 0> -> fs 15. [s 7, [x, s 10]], <P: s> -> fs 15. [s 8, [[o, e], s 11]], e -> s 16. [s 9, [['N', s], s 12]], (no arcs) [s 10, [['N', e], s 13]], <N: 0> -> s 12. [s 11, [s, s 14]], [s 12, [['P', 0], fs 15]], [s 13, [['P', s], fs 15]], [s 14, [e, s 16]], [fs 15, noarcs], [s 16, [['N', 0], s 12]] ]).

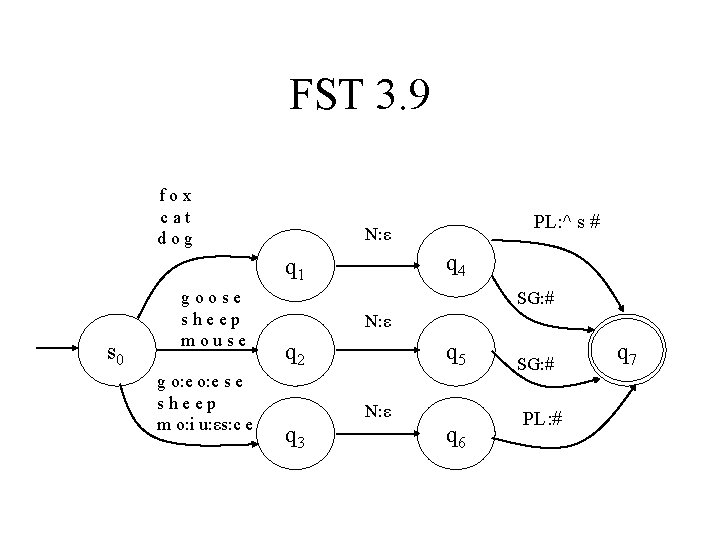
FST 3. 9 fox cat dog q 4 q 1 s 0 goose sheep mouse g o: e s e sheep m o: i u: εs: c e PL: ^ s # N: ε SG: # N: ε q 2 q 5 N: ε q 3 q 6 SG: # PL: # q 7

FST 3. 9 (portion) fox cat dog [s 0, [f, s 1], [c, s 3], [d, s 5]], [s 1, [o, s 2]], [s 2, [x, q 1]], [s 3, [a, s 4]], [s 4, [t, q 1]], [s 5, [o, s 6]], [s 6, [g, q 1]], q 1 s 0 f s 0 c d s 1 s 3 s 5 o a o s 2 s 4 s 6 x t g q 1