Especificaes de Filtros Resposta em frequncia de um















- Slides: 25

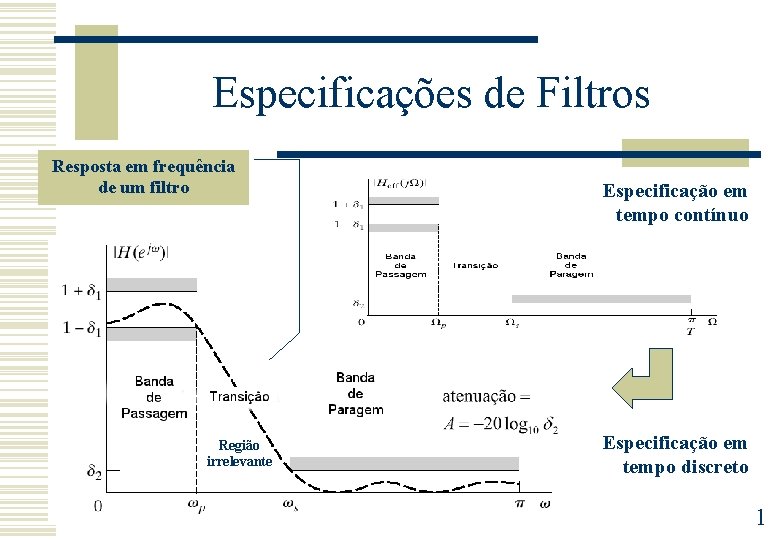
Especificações de Filtros Resposta em frequência de um filtro Região irrelevante Especificação em tempo contínuo Especificação em tempo discreto 1

FIR – Finite Impulse Response Filter (Resposta ao Impulso Finita) Coeficientes da resposta impulsiva do filtro Só tem zeros sempre estáveis M – ordem do filtro (ordem do polinómio H(z)) Numero de coeficientes é do filto é M+1=N 2

IIR – Infinite Impulse Response Filter (Resposta ao Impulso Infinita) Corresponde a uma equação às diferenças. Implementa uma equação às diferenças em que a saida não depende directamente apenas de valores passados da entrada mas tambem da saida. Contêm zeros e pólos Sistemas recursivos N – ordem do filtro Ordem do polinomio no denominador 3

FIR vs IIR w FIR n n n São sempre estáveis Permitem facilmente fase linear Podem necessitar de ordem elevada w IIR n Menor peso computacional 4

Projecto de Filtros FIR Método da Janela Especificação de uma resposta ideal na frequência e determinação da resposta impulsiva correspondente (teoricamente ou numericamente (IFFT)): Multiplicação por janela: Atraso da janela Janela rectangular: janela Pode ser infinita e não causal truncagem 5

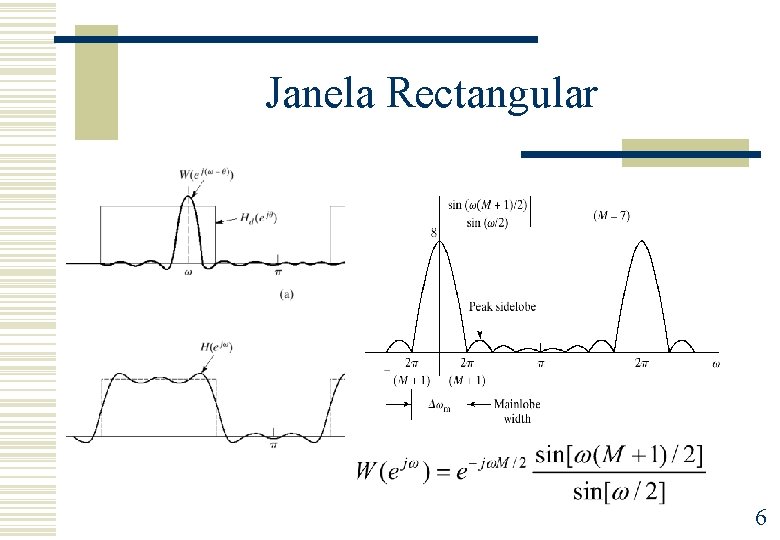
Janela Rectangular 6

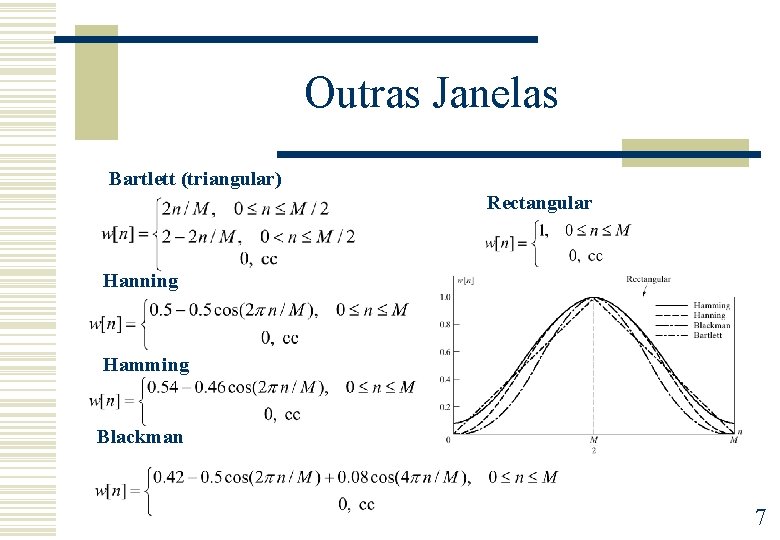
Outras Janelas Bartlett (triangular) Rectangular Hanning Hamming Blackman 7

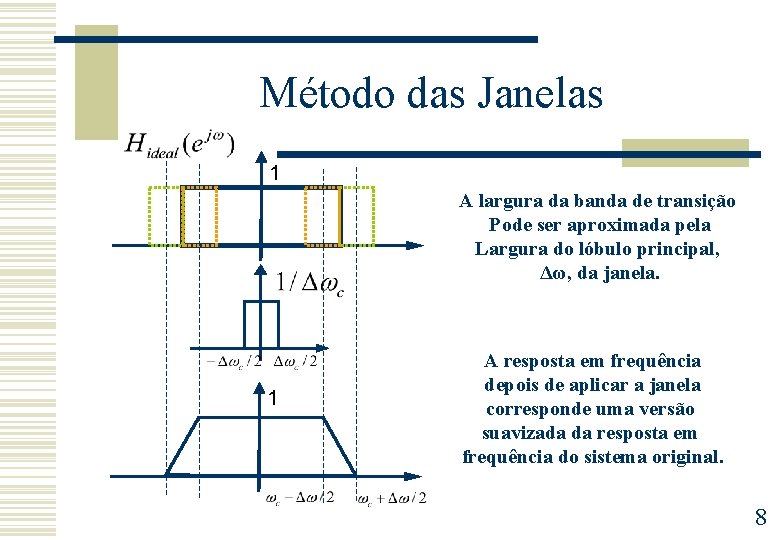
Método das Janelas 1 A largura da banda de transição Pode ser aproximada pela Largura do lóbulo principal, Δω, da janela. 1 A resposta em frequência depois de aplicar a janela corresponde uma versão suavizada da resposta em frequência do sistema original. 8

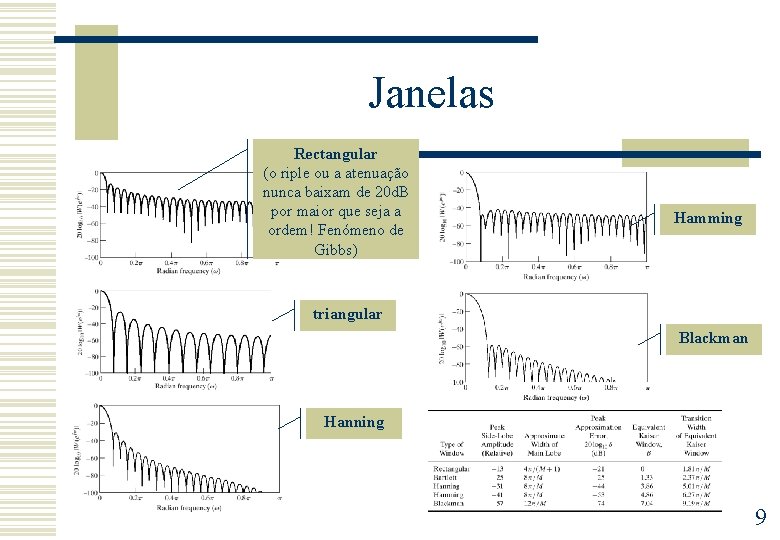
Janelas Rectangular (o riple ou a atenuação nunca baixam de 20 d. B por maior que seja a ordem! Fenómeno de Gibbs) Hamming triangular Blackman Hanning 9

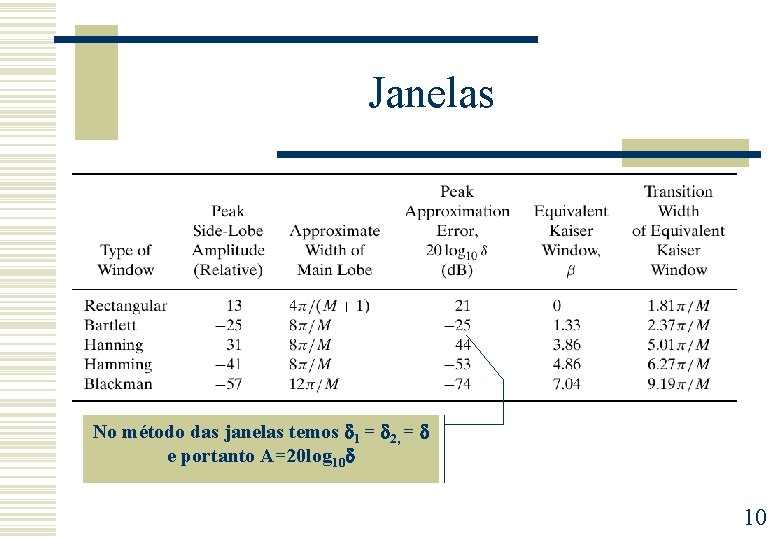
Janelas No método das janelas temos 1 = 2, = e portanto A=20 log 10

Janela de Hanning WR – Janela Rectangular W – Janela Hanning 11

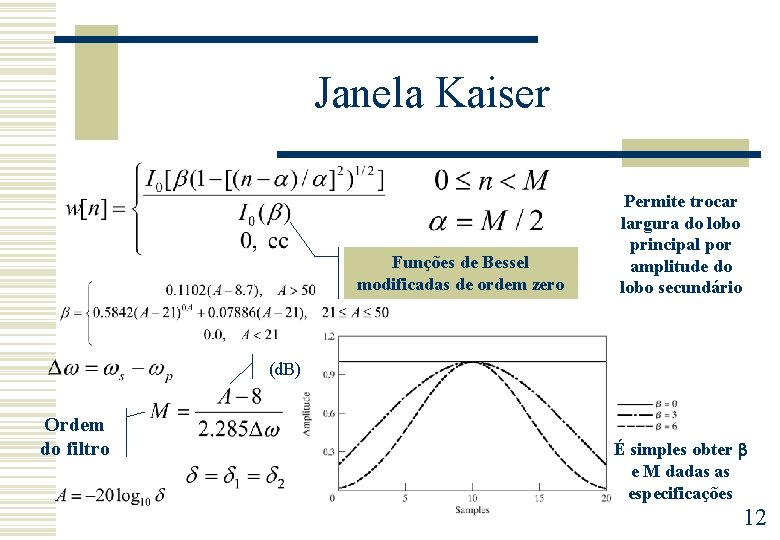
Janela Kaiser Funções de Bessel modificadas de ordem zero Permite trocar largura do lobo principal por amplitude do lobo secundário (d. B) Ordem do filtro É simples obter e M dadas as especificações 12

Ex: Projecto Diferenciadores em tempo discreto w A resposta em frequência de um diferenciador ideal será, Nota: Tal corresponderá a amostragem do sinal derivada de um sinal de entrada amostrado dentro dos limites do crtitério de Nyquist A que corresponde um diferenciador com resposta impulsiva dada por: Notar que: Notar os limitações de aplicação!!! 13

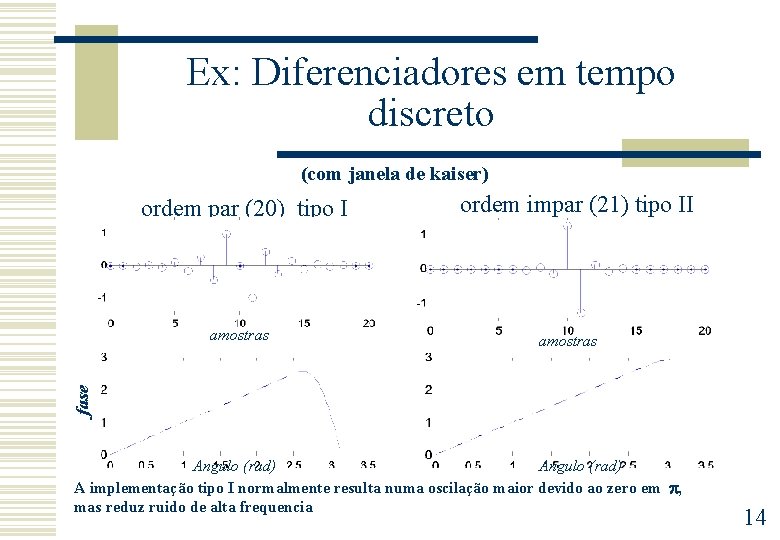
Ex: Diferenciadores em tempo discreto (com janela de kaiser) ordem par (20) tipo I amostras fase amostras ordem impar (21) tipo II Angulo (rad) A implementação tipo I normalmente resulta numa oscilação maior devido ao zero em , mas reduz ruido de alta frequencia 14

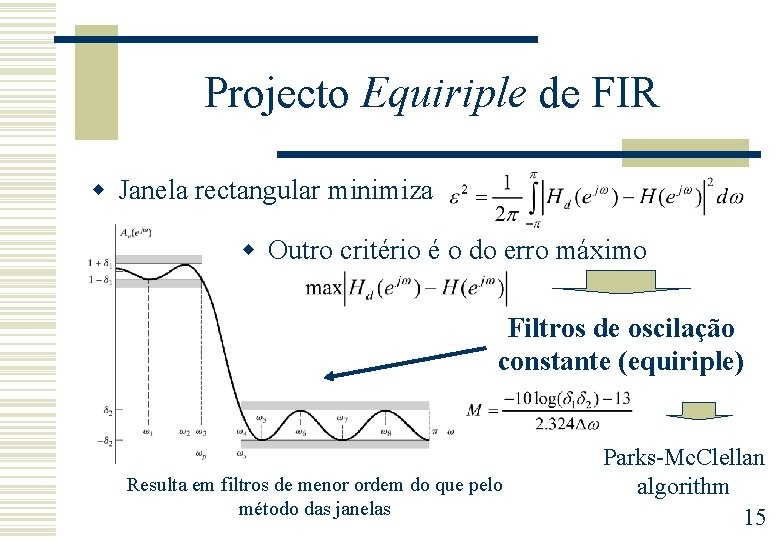
Projecto Equiriple de FIR w Janela rectangular minimiza w Outro critério é o do erro máximo Filtros de oscilação constante (equiriple) Resulta em filtros de menor ordem do que pelo método das janelas Parks-Mc. Clellan algorithm 15

Projecto Equiriple w Erro quadrático mínimo (janela rectangular) n Óptimo sinais de banda larga, ex: ruído branco w Equiriple (erro máximo mínimo) n n Garante qualquer sinal fora da banda é atenuado pelo menos A d. B Projecto para o pior caso, ie, sinais de banda estreita junto à banda de transição 16

Projecto de Filtros IIR Conversão de Filtros Analógicos • Aproveita os resultados sistemas analógicos Transformação Bilínear Provoca uma transformação na frequência • Um mapa do plano-s para o plano-z Mapa exacto seria (AD->DSP->DA): 17

Transformação Bilínear Transforma o semi-plano complexo esquerdo no circulo unitário! Sistemas estáveis resultam em sistemas estáveis Transformação na frequência: Especificações devem ser ajustadas de forma a compensar a transformação 18

Transformação bilinear w A transformação bilinear corresponde a utilização de um método de integração trapezoidal Função de transferência de um integrador Área do trapézio 19

Invariância ao Impulso amostragem 20

Filtros Butterworth w São filtros que têm uma característica de amplitude maximamente plana na banda de passagem. Têm a seguinte resposta em amplitude: A sua transformada de Laplace é constituída apenas por pólos nas posições: 21

Filtros Chebyshev w Permitem oscilações na banda de passagem de forma permitir a utilização de filtros de menor ordem relativamente ao Butterworth. 22

Comparação de Filtros IIR w Butterworth n Resposta em frequência maximamente plana w Chebyshev n Maior atenuação mas pior resposta de fase w Qualquer deles tem distorção de fase ao contrário dos filtros FIR que têm fase linear! 23

Filtros passa-banda Projecto em tempo continuo w Transformação passa-baixo passa banda w Escolher o tal que, w Especificações ou mais apertadas 24

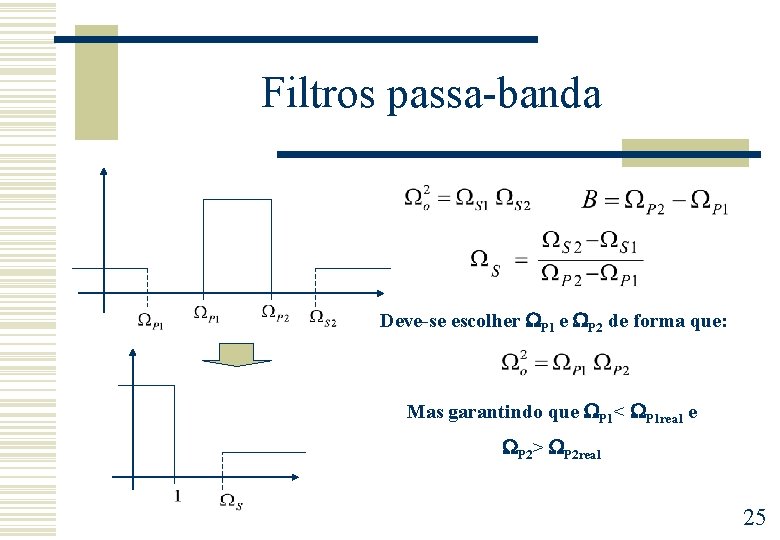
Filtros passa-banda Deve-se escolher P 1 e P 2 de forma que: Mas garantindo que P 1< P 1 real e P 2> P 2 real 25
 Senoide amortecida
Senoide amortecida Locução adjetiva olhos felinos
Locução adjetiva olhos felinos Filtros analogicos
Filtros analogicos Filtro rapido
Filtro rapido Qué es un macro filtro
Qué es un macro filtro Filtros ideales
Filtros ideales Filtros rayos x
Filtros rayos x Desventajas de la filtración
Desventajas de la filtración A resposta
A resposta Resposta
Resposta Taquicardia supraventricular
Taquicardia supraventricular Elias pediu emprestado
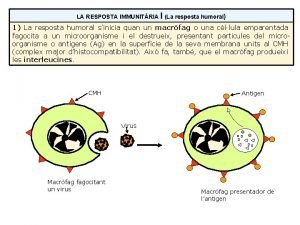
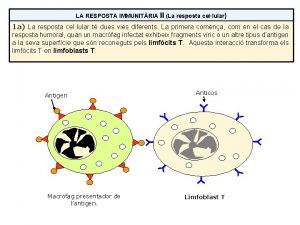
Elias pediu emprestado Macrofago e monocito
Macrofago e monocito Instrumentos de entrevista
Instrumentos de entrevista Uosm posm
Uosm posm Imune celular
Imune celular Charadas com respostas
Charadas com respostas Qual e a resposta
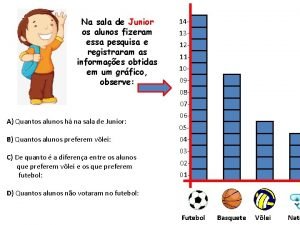
Qual e a resposta Observe o grafico de brinquedos de artur
Observe o grafico de brinquedos de artur Resposta
Resposta Qual a resposta
Qual a resposta Assinale a melhor resposta em papagaio temos
Assinale a melhor resposta em papagaio temos Horizontal resposta
Horizontal resposta Resposta
Resposta Resposta
Resposta Resposta
Resposta