Errors Transmission errors are a way of life

Errors • Transmission errors are a way of life. • In the digital world an error means that a bit value is flipped. • An error can be isolated to a single bit. • Errors on some media come in bursts – Harder to detect and correct than isolated errors. 3/3/2021 Errors 1

Dealing with Errors • Error detecting codes – provide enough redundant information to enable the receiver to deduce that an error occurred • Error correcting codes – provide enough redundant information to enable the receiver to deduce that an error occurred AND how to fix it • So a message consists of m data bits and r redundant or check bits. 3/3/2021 Errors 2

Hamming Distance • Hamming distance: – the number of bit positions in which two codewords differ • Simple to calculate find the XOR • If two codewords are a Hamming distance d apart, it will require d single-bit errors to convert one into the other. • The Hamming distance of a code is the minimum Hamming distance between any two codewords. 3/3/2021 Errors 3

Hamming Distance 2 Code 000 011 101 110 Note that not all of the 8 different bit patterns are included in the code Any single error will convert a valid codeword into an invalid codeword. If we know the valid codewords we can detect the error 3/3/2021 Errors 4

How Error Detection Works 2 e Valid codeword Invalid Code Words 3/3/2021 Errors 5

Parity • A simple single error detecting code could be constructed by counting bits. – Any codeword with an even number of bits is consider valid (you could also make it the other way around). • The minimum distance of this code is 2, so it is capable of detecting single errors. • This code can be created by adding a parity bit: – chose the parity bit so that the number of ones in the codeword is even (or odd). 3/3/2021 Errors 6

Parity in Action Want to send: 10 Receive: 111 (ERROR) Data Link Sends: 110 3/3/2021 Errors 7

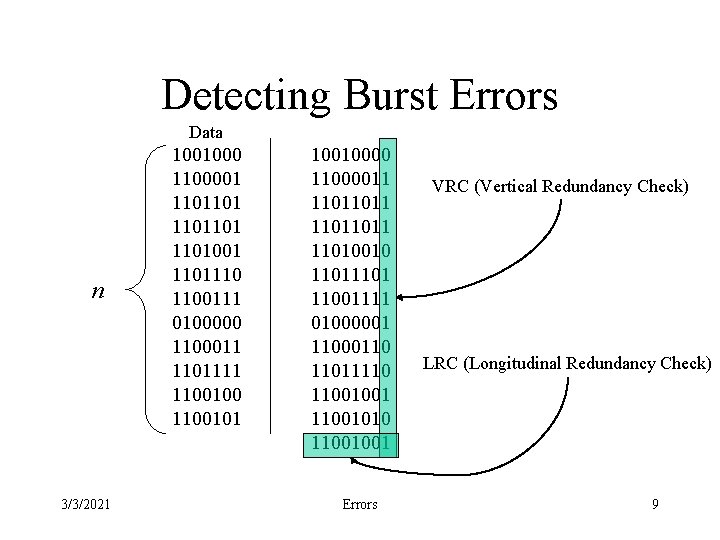
Protecting Blocks • The probability of detecting a burst error on a block using a single parity bit is 50%. • This can be improved by viewing the block as a n by k bit matrix. • A parity bit is then computed for each column. • The check bits are placed in a k-bit row and affixed to the matrix as the last row. • Bursts of length n can be detected. 3/3/2021 Errors 8

Detecting Burst Errors Data n 3/3/2021 1001000 1100001 1101101001 1101110 1100111 0100000 1100011 1101111 1100100 1100101 10010000 11000011 11011011 11010010 1101 11001111 01000001 11000110 11011110 11001001 11001010 11001001 Errors VRC (Vertical Redundancy Check) LRC (Longitudinal Redundancy Check) 9

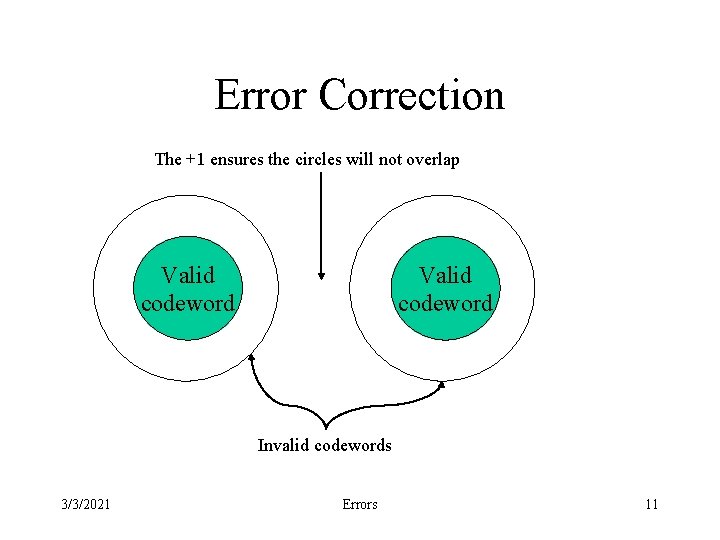
What About Error Correction? • How do we get error correction? – Must increase the minimum distance of the code • The key to error correction is that it must be possible to detect and locate the error. • The minimum distance must be at least 2 e+1 3/3/2021 Errors 10

Error Correction The +1 ensures the circles will not overlap Valid codeword Invalid codewords 3/3/2021 Errors 11

A Simple Single Error Correcting Code 3/3/2021 Errors 12

Hamming Codes • Hamming codes are n-bit codes that can correct single errors. • The basic idea is to split the codeword into two portions – information or message bits (m) – parity bits (k) • The result are codewords that consist of m+k bits 3/3/2021 Errors 13

Choosing m and k • Selecting m is easy, you are usually told what it is. • How do you pick k? • The parity bits are used to generate a k-bit word that identifies where in the codeword the error, if any, occurred. • Consequently, k must satisfy the following: 3/3/2021 Errors 14

Constructing the Codeword • The codeword consists of m+k bits. • The location of each of the m+k bits is assigned a decimal value, 1 is assigned to the MSB, and m+k to the LSB. • Parity bits go in positions 1, 2, 4, …, 2 k-1 p 0 p 1 m 0 p 2 m 1 m 2 m 3 p 3 m 4. . . mm+k 1 3/3/2021 2 3 4 5 6 Errors 7 8 9 . . . m+k 15

Parity Checks • The parity checks must be specified so that when an error occurs, the position number will take on the value assigned to to location of the error 3/3/2021 Errors 16

Putting It Together 3/3/2021 Errors 17

Example Send the message 0010 using a hamming code Step 1: Find k. Here k=3 Step 2: Determine where things go Step 3: Figure out the parity bits p 1 will cover 1, 3, 5, 7, 9, 11, … p 2 will cover 2, 3, 6, 7, 10, 11, … p 3 will cover 4, 5, 6, 7, 12, 13, 14, 15, . . . 3/3/2021 Errors 18

Correcting Burst Errors • Hamming codes can be used to correct burst errors • A sequence of s consecutive codewords are arranged as a matrix, one codeword per row. • Transmit data one column (s bits) at a time. • The matrix is reconstructed by the receiver one column at a time. • If a burst error of size s occurs, only a single column will be affected. 3/3/2021 Errors 19

Correcting Burst Errors Character ASCII H a m m I n g 1001000 1100001 1101101001 1101110 1100111 0100000 1100011 1101111 1100100 1100101 c o d e 3/3/2021 Check Bits Errors 00110010000 10111001001 11101010101 01101011001 01101010110 01111001111 10011000000 11111000011 1010101111100 00111000101 s 20

Correcting vs. Detecting • Most often error detection followed by retransmission is more efficient. • Consider a channel with an error rate is 10 -6 per bit (one error per million bits sent) – Block size 1000 == 10 check bits ( k == 10 ) – For parity one check bit will suffice • Overhead for sending 1 MB – Hamming == 10, 000 bits – Parity == 2001 bits (since 1 block will be retransmitted) 3/3/2021 Errors 21

Checksums • Both sides agree on a checksum function • Sender – Computes checksum while sending message – Attaches result to the end of the message • Receiver – Computes checksum while reading message – Compares result to checksum at end of message 3/3/2021 Errors 22

Error Detection 3/3/2021 Errors 23

Simple Example • Checksum function – Sum of bytes in message modulo 256 • Sender – 72 101 108 111 87 111 114 108 100 – Checksum 1020 % 256 252 – 72 101 108 111 87 111 114 108 100 252 • Receiver – 72 101 118 108 111 87 111 114 108 100 252 – Checksum 1030 % 256 6 – Error, discard message 3/3/2021 Errors 24

Cyclic Redundancy Check • CRC detects all of the following errors: – All single bit errors – All double bit errors if the divisor is at least three terms – Any odd number of errors, if the divisor contains a factor (x+1) – Any error in which the length of the error (an error burst) is less than the length of the FCS – Most errors with larger bursts 3/3/2021 Errors 25

Basic Idea • Treat the entire message as a binary number • To calculate the checksum – Divide message by another fixed number – Use the remainder as the checksum • CRC treats bit strings as representations of polynomials with coefficients of 0 and 1. – 110001 == x 5+ x 4+ x 0 3/3/2021 Errors 26

The Generator Polynomial • Both the sender and the receiver must agree upon a generator polynomial, G(x). – Both the high and low order bits of the generator must be 1. – The length of the generator is one bit longer than the FCS. – Finally the frame must be longer than the generator. • This is what we use mathematicians for 3/3/2021 Errors 27

Standard Polynomials • CRC-12 (x 12+x 11+x 3+x 2+x 1+1) – used when the character length is 6 • CRC-16 (x 16+x 15+x 2+1) • CRC-CCITT (x 16+x 12+x 5+1) – – 3/3/2021 used for 8 bit characters catches all single and double errors all errors of an odd length all bursts of 16 -bits or less, 99. 997% of 17 -bits, and 99. 998% of 18 -bits and longer. Errors 28

The Algorithm • To compute the checksum – Append n 0 s to the end of the message, where n is the number of bits in the checksum – The resulting value is divided by the generator polynomial – Each division step is carried out in the conventional manner, except that we use polynomial arithmetic 3/3/2021 Errors 29

Polynomial Arithmetic • Subtraction and addition as usual but no borrows or carries 1 -1 -0 -1 -1 0 -0 -0 1 +1 -0 1 +0 -1 0 +1 -1 0 +0 -0 • Both operations are identical to XOR 3/3/2021 Errors 30

Polynomial Arithmetic • Addition and subtraction, are a single operation, that is its own inverse • By collapsing addition and subtraction, the arithmetic discards any notion of magnitude – Beyond the power of the highest bit • 1010 is clearly greater than 10 • 1010 is no longer greater than 1001 – 1010 = 1001 + 0011 – 1010 = 1001 - 0011 3/3/2021 Errors 31

Polynomial Multiplication 1101 x 1011 ---11010 000000 1101000 ------1111111 3/3/2021 Errors 32

Polynomial Division 1101 1011 1111111 1001 1011 0 3/3/2021 Errors 33

The Algorithm (continued) • The division produces a quotient which is discarded. • The remainder replaces the 0 s appended to the frame (subtracted from the frame modulo 2). • The resulting frame is now evenly divisible by the generator polynomial. • The receiver performs the same division, a nonzero remainder indicates that an error occurred. 3/3/2021 Errors 34

CRC Example (transmit) Frame contents: Polynomial: Frame with 0 s: 111011 11101 (x 4+ x 3+x 2 + x 0) 11101100001 1110110000 11101 ----1101 Frame to send: 3/3/2021 11101 Errors 35

CRC Example (receive) Frame contents: Polynomial: 11101 (x 4+ x 3+x 2 + x 0) 100001 1110111101 ----0 3/3/2021 Errors 36

Fast Polynomial Division 3/3/2021 Start 0000000 1111111 0000000 Shift 0000001 1111110 0000000 Shift 0000011 1111100 0000000 Shift 0000111 1111000 0000000 Shift 0001111 1110000000 XOR/Inc 0000100 1110000001 Shift 0001001 110000010 XOR/Inc 0000010 110000011 Shift 0000101 1000000110 Shift 0001011 0000000 0001100 XOR/Inc 0000000 0001101 Errors 37

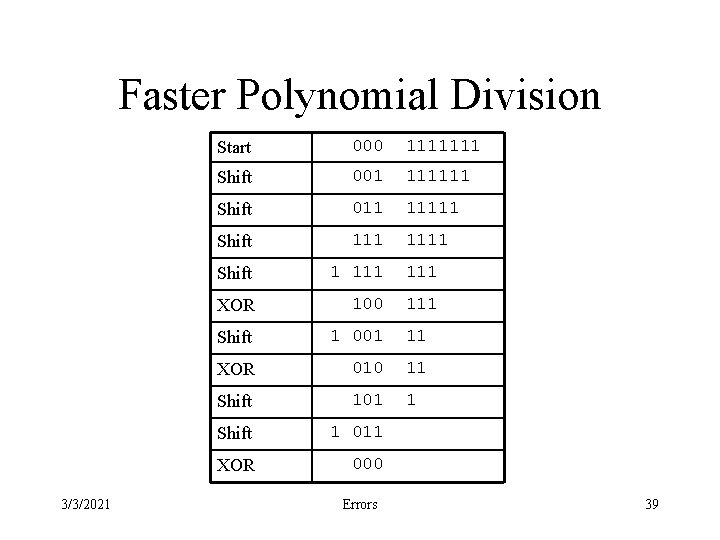
Optimize • For CRC – We do not need the quotient – If the divisor is W bits long • The remainder will be at most W-1 bits long • Only need 1 register 3/3/2021 Errors 38

Faster Polynomial Division 3/3/2021 Start 000 1111111 Shift 001 111111 Shift 011 11111 Shift 1 111 XOR 100 111 Shift 1 001 11 XOR 010 11 Shift 101 1 Shift 1 011 XOR 000 Errors 39

CRC Simple Version • Consider the polynomial 10111 with a CRC of size W=4 • To perform the division perform the following: – Load the register with zero bits. – Augment the message by appending W zero bits to the end of it. – While (more message bits) • Shift the register left by one bit, reading the next bit of the augmented message into register bit position 0. • If (a 1 bit popped out of the register during step 3) – Register = Register XOR Poly. • The register contains the remainder. Source: http: //www. repairfaq. org/filipg/LINK/F_crc_v 33. html 3/3/2021 Errors 40