Entropy Change at Constant Volume For an ideal

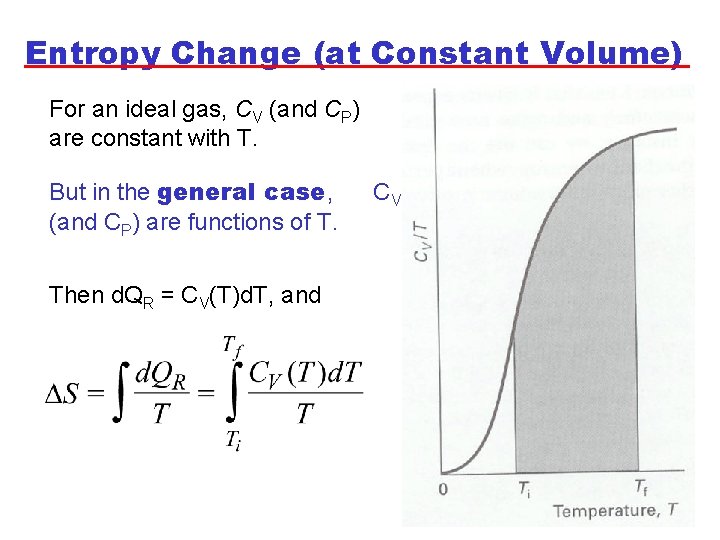
Entropy Change (at Constant Volume) For an ideal gas, CV (and CP) are constant with T. But in the general case, (and CP) are functions of T. Then d. QR = CV(T)d. T, and CV

Kinetic Model of Gas molecules typically collide with a wall or other molecules about once every ns. Each molecule has a different speed, si. For N molecules, the root-meansquare (rms) speed, c, is: ( ) If n moles of gas, with a molar mass of M, are in a volume of V, then the pressure is: Total mass

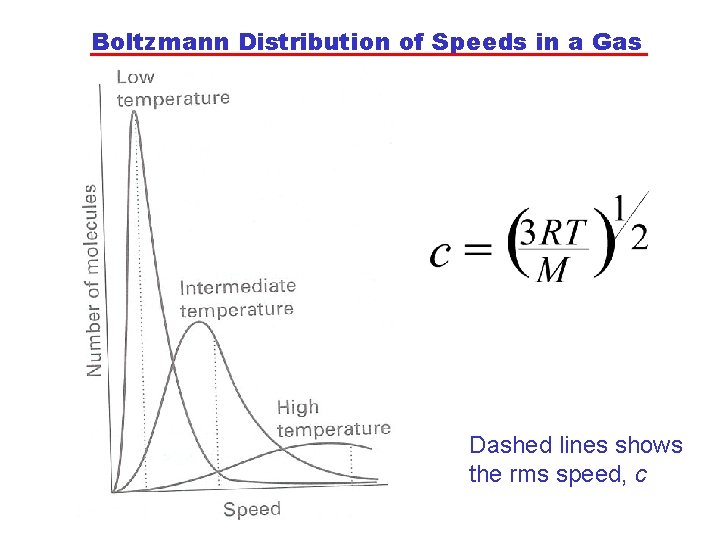
Kinetic Model of Gas As PV=n. RT for an ideal gas, we can solve for c as a function of T: There is a proportionality between the rms speed of molecules and the square root of temperature. Note: There is a distribution of speeds, which is described by the Boltzmann distribution.

Boltzmann Distribution of Speeds in a Gas Dashed lines shows the rms speed, c

Statistical Approach • Statistical thermodynamics uses a mathematical description of the distribution of particle positions and speeds to calculate the state variables for a system and to obtain values of the state functions, such as U and S. • The position of each molecule is given in “phase space” by the co-ordinates of x, y and z. • The momentum (product of mass and velocity) of each molecule is represented in “phase space” by three vectors: px, py and pz. • Neither position nor momentum can both be known with certainty but are only known within a range in phase space.

Statistical Approach • The positions of molecules in phase space can be used to determine the bulk state variables for the system. • Obvious correlation between positions and volume, V. • Pressure can be related to the rms speed which is related to momentum of all the molecules in the system. • Temperature is related to the square of the rms speed, which is likewise related to the momentum. • Several different arrangements of molecules in phase space can correspond to the same bulk state (P, V, T). • The number of arrangements of molecules for a particular state of the systems is called thermodynamic probability, .

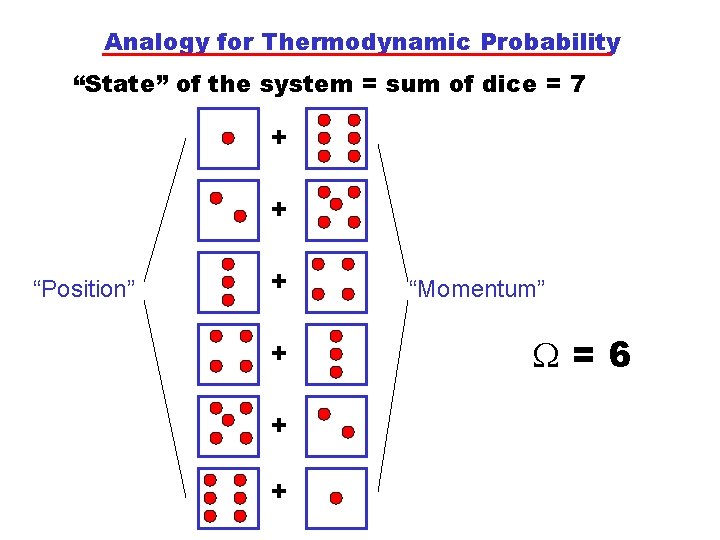
Analogy for Thermodynamic Probability “State” of the system = sum of dice = 7 + + “Position” + + “Momentum” =6

Analogy for Thermodynamic Probability “State” of the system = sum of dice = 2 + =1 • Conclude that a “state” of 7 is more likely to be found as it has a higher probability, . • In a “real” system, each state (Pi, Vi, Ti) will have a certain i. • As one mole contains ~1023 molecules, tends to be a very large number! • The equilibrium state of a system is most likely and hence must have the largest .

Relationship between and S • In an isolated system, or thermodynamic Universe, molecules will spontaneously move from a low state to a high state. • Thus the for the system approaches a maximum. • Previously we saw that in a thermally-isolated system (or t. d. Universe), S approaches a maximum. • CONCLUDE that there must be some proportionality between and S.

Boltzmann Equation For a thermodynamic Universe, we saw that: SUniverse The Universe can consist of several parts (systems and reservoirs) each with their own entropy, so: SUniverse = S 1 + S 2 + S 3 +. . . Probabilities are multiplicative, so: SUniverse = S 1 + S 2 + S 3 +. . . 1 2 3…. But, since S 1 1 and S 2 2 , etc. , then: S 1 + S 2 + S 3 +. . . 1+ 2+ 3+. . . How can this be? Boltzmann thought about this problem….

Boltzmann Equation We note a property of logarithms: ln 1+ ln 2+ ln 3+. . . ln ( 1 2 3…. ) The conditions are therefore satisfied if S ln . Then, S 1 + S 2 + S 3 +. . . ln 1+ ln 2+ ln 3+. . . but also S 1 + S 2 + S 3 +. . . ln( 1 2 3…. ), as required. Boltzmann derived a relationship in which k is the constant of proportionality: S = k ln with k = 1. 38 x 10 -23 JK-1. Voted one of the ten most beautiful equations in a survey by Physics World!