Mutual Information Joint Entropy Conditional Entropy Contents Entropy

  • Slides: 13
Download presentation
Mutual Information, Joint Entropy & Conditional Entropy

Mutual Information, Joint Entropy & Conditional Entropy

Contents Entropy Joint entropy & conditional entropy Mutual information 2

Contents Entropy Joint entropy & conditional entropy Mutual information 2

Entropy(1/2) Entropy(self-information) the amount of information in a random variable average uncertainty of a

Entropy(1/2) Entropy(self-information) the amount of information in a random variable average uncertainty of a random variable the average length of the message needed to transmit an outcome of that variable the size of the search space consisting of the possible values of a random variable and its associated probabilities Properties ( : providing no new information) increases with message length 3

Entropy(2/2) - Example Simplified Polynesian letter frequencies per-letter entropy coding p 100 t 00

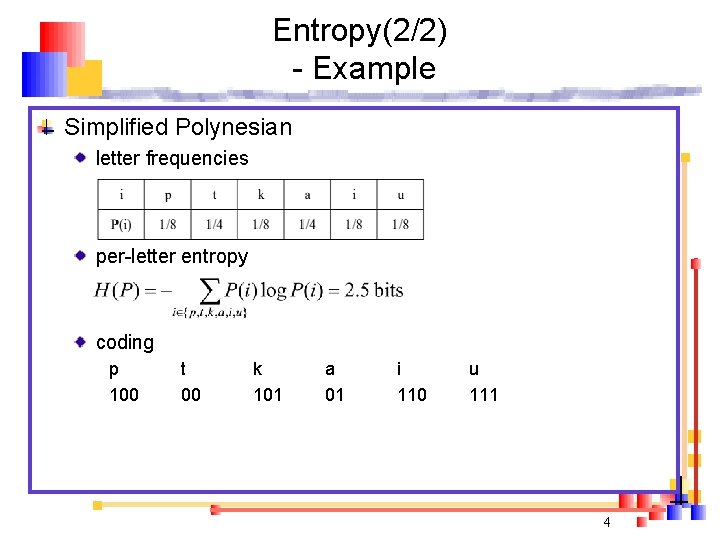
Entropy(2/2) - Example Simplified Polynesian letter frequencies per-letter entropy coding p 100 t 00 k 101 a 01 i 110 u 111 4

Joint Entropy & Conditional Entropy(1/4) Joint Entropy the amount of information needed on average

Joint Entropy & Conditional Entropy(1/4) Joint Entropy the amount of information needed on average to specify both their values Conditional Entropy how much extra information you still need to supply on average to communicate Y given that the other party knows X 5

Joint Entropy & Conditional Entropy(2/4) Chain Rules for Entropy 6

Joint Entropy & Conditional Entropy(2/4) Chain Rules for Entropy 6

Joint Entropy & Conditional Entropy(3/4) - Example Simplified Polynesian Revisited syllable structure all words

Joint Entropy & Conditional Entropy(3/4) - Example Simplified Polynesian Revisited syllable structure all words consist of sequences of CV syllables. C: consonant, V: vowel 7

Joint Entropy & Conditional Entropy(4/4) Entropy Rate(per-word/per-letter entropy) Entropy of a Language 8

Joint Entropy & Conditional Entropy(4/4) Entropy Rate(per-word/per-letter entropy) Entropy of a Language 8

Mutual Information(1/2) Mutual Information the reduction in uncertainty of one random variable due to

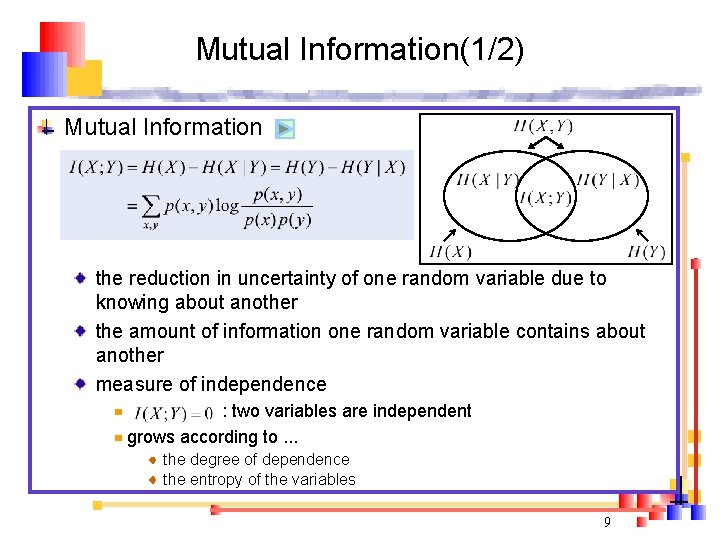
Mutual Information(1/2) Mutual Information the reduction in uncertainty of one random variable due to knowing about another the amount of information one random variable contains about another measure of independence : two variables are independent grows according to. . . the degree of dependence the entropy of the variables 9

Mutual Information(2/2) Conditional Mutual Information Chain Rule Pointwise Mutual Information between two particular points

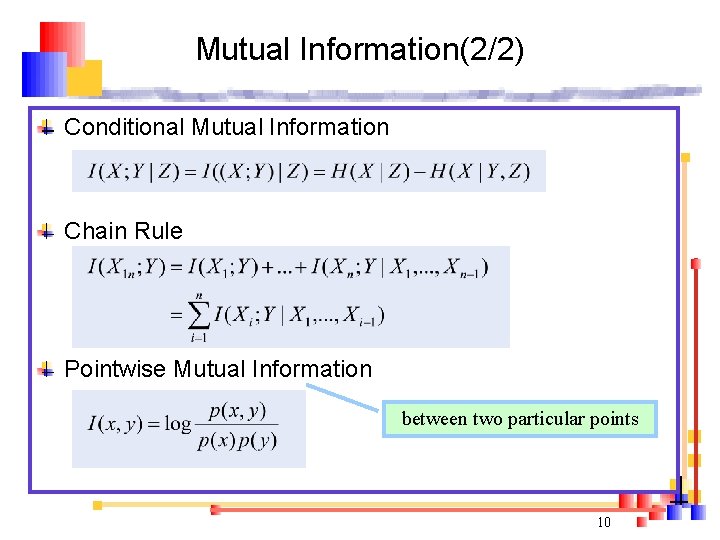
Mutual Information(2/2) Conditional Mutual Information Chain Rule Pointwise Mutual Information between two particular points 10

The Noisy Channel Model(1/2) The Noisy Channel Model Message from a finite alphabet Encoder

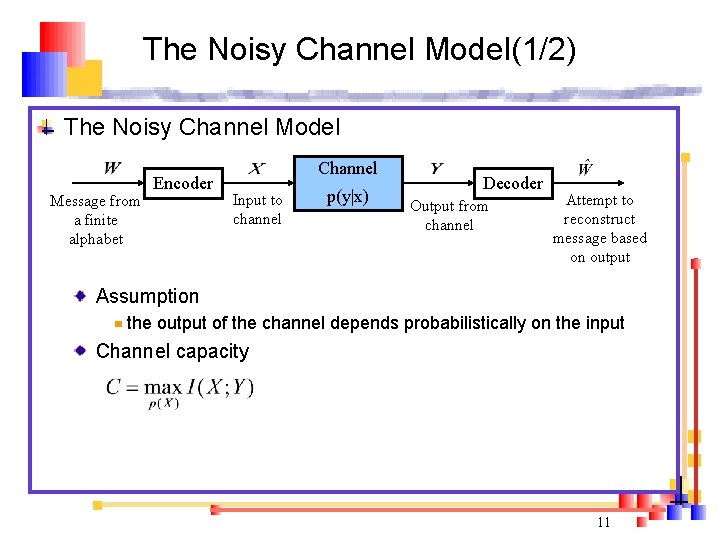
The Noisy Channel Model(1/2) The Noisy Channel Model Message from a finite alphabet Encoder Channel Input to channel p(y|x) Decoder Output from channel Attempt to reconstruct message based on output Assumption the output of the channel depends probabilistically on the input Channel capacity 11

The Noisy Channel Model(2/2) The Noisy Channel Model in Linguistics Noisy Channel Decoder decode

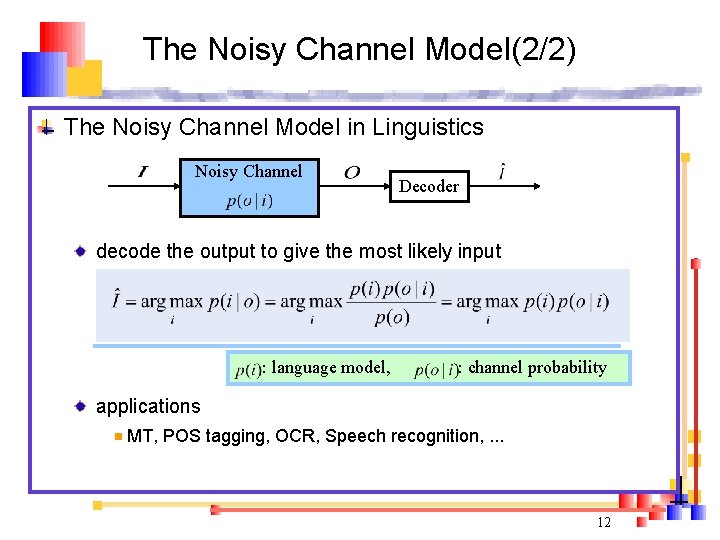
The Noisy Channel Model(2/2) The Noisy Channel Model in Linguistics Noisy Channel Decoder decode the output to give the most likely input : language model, : channel probability applications MT, POS tagging, OCR, Speech recognition, . . . 12

Derivation of Mutual Information 13

Derivation of Mutual Information 13

CONDITIONAL CLAUSES Conditional Sentences First Conditional Real ConditionalCONDITIONAL CLAUSES Conditional Sentences First Conditional Real Conditional
FED TAPERING MUTUAL FUNDS Understanding Mutual Funds MUTUALFED TAPERING MUTUAL FUNDS Understanding Mutual Funds MUTUAL
FED TAPERING MUTUAL FUNDS Understanding Mutual Funds MUTUALFED TAPERING MUTUAL FUNDS Understanding Mutual Funds MUTUAL
Conditional Density Functions and Conditional Expected Values ConditionalConditional Density Functions and Conditional Expected Values Conditional
FIRST CONDITIONAL First conditional We use first conditionalFIRST CONDITIONAL First conditional We use first conditional
Conditional Statements 1 Conditional Statement Definition A conditionalConditional Statements 1 Conditional Statement Definition A conditional
Nested conditional statements Nested conditional statements A conditionalNested conditional statements Nested conditional statements A conditional
CONDITIONAL SENTENCE Conditional Sentence Conditional sentences are sentencesCONDITIONAL SENTENCE Conditional Sentence Conditional sentences are sentences
Conditional Statements Conditional Statements A CONDITIONAL STATEMENT isConditional Statements Conditional Statements A CONDITIONAL STATEMENT is
Conditional 1 2 7 CONDITIONAL 1 CONDITIONAL 2Conditional 1 2 7 CONDITIONAL 1 CONDITIONAL 2
Conditional Jump Conditional Loop Instructions and Conditional StructuresConditional Jump Conditional Loop Instructions and Conditional Structures
CONTROL STRUCTURES CONDITIONAL CONTROLS Conditional Control Conditional controlCONTROL STRUCTURES CONDITIONAL CONTROLS Conditional Control Conditional control