Chapter 7 Applications of the Second Law 1

Chapter 7. Applications of the Second Law 1

Consider entropy changes in various reversible (!!!) processes We have: đ đ (a) Adiabatic process đ Hence a reversible adiabatic process is isentropic. (b) Isothermal process: đ (c) Change of phase (isothermal and isobaric) In this case the energy transfer as heat is the latent heat of transformation, so (d) Isochoric process. In general u=u(v, T) and so, for an isochoric process u=u(T) and 2

From (1) If the specific heat is constant over the temperature range of interest (isochoric) (e) Isobaric process: In isobaric processes it is often convenient to employ the enthalpy. The 1 st Law is: so Using equation (2) to eliminate du 3

Consider h=h(P, T) Since we are considering the case P=constant Placing this in equation (3) For constant specific heat (isobaric) 4

Entropy of an ideal gas n Although it is possible to determine an absolute value for the entropy, we do not do so at the present time. We have already shown for an ideal gas (students should review): Q = CPd. T - Vd. P _ _ _ (1) đ Q = CVd. T + Pd. V _ _ _(2) đ Note that from (1) and so -------(1 a) Similarly ------(2 a) 5

Introducing molar quantities and integrating equation (1 a): Similarly, using equation (2 a): From this last equation we deduce the following: (a) V fixed: the greater the temperature rise , the greater the increase in entropy. (b) T fixed: the greater the volume expansion, the greater the increase in entropy 6

Although we have been considering an ideal gas, these conclusions hold quite generally. Consider, for example, an isentropic expansion of a gas. The increase in volume will result in an increase in the entropy. This increase must be balanced by an equal decrease and this must come about by a drop in temperature. 7

n T S Diagrams A convenient representation of processes involving reversible cycles for various heat engines is a diagram with T along the y-axis and S along the x-axis. For an isothermal process the curve (isotherm) will be a straight horizontal line. For an adiabatic process, since đQ = 0 and so d. S = 0, the curve (isentrope) will be a straight vertical line. 8

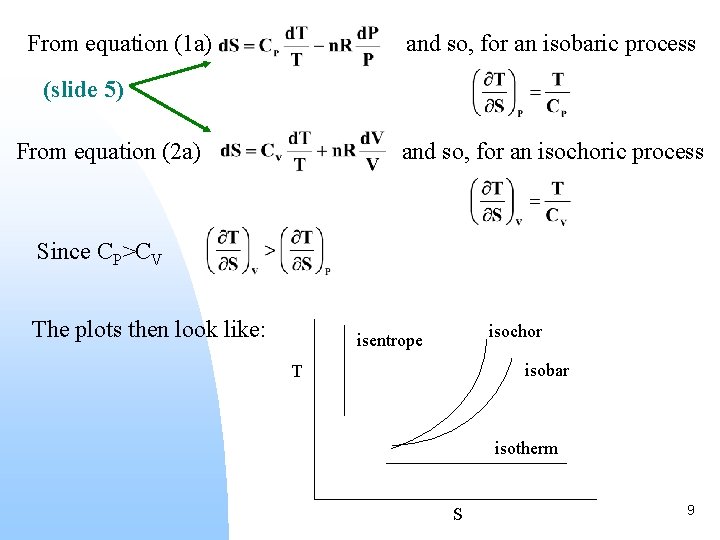
From equation (1 a) and so, for an isobaric process (slide 5) From equation (2 a) and so, for an isochoric process Since CP>CV The plots then look like: isochor isentrope isobar T isotherm S 9

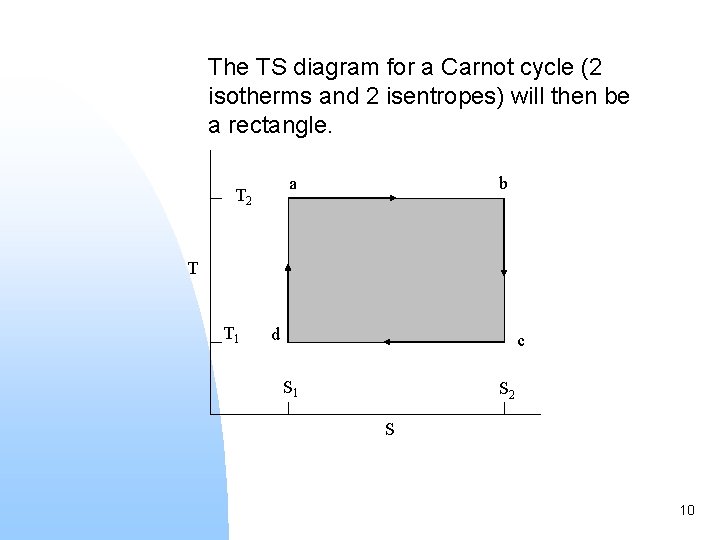
The TS diagram for a Carnot cycle (2 isotherms and 2 isentropes) will then be a rectangle. a T 2 b T T 1 d c S 1 S 2 S 10

Area under ab is the heat absorbed (Q 2) by system. Area under cd is the heat rejected (Q 1) by system. The shaded area is then the work done during the cycle. W = Q 1 + Q 2 and the efficiency, graph. Remember that is negative. Remember that, with a PV diagram, the area under the curve is W. We wish to consider all the entropy changes which take place when there is a reversible exchange of energy between a system and its surroundings d. S (system) + d. S (surroundings) = d. S (universe) 11

The temperature of the system and its surrounding differ by only an infinitesimal amount at any time. Suppose the surroundings (reservoir) absorbs an amount of heat đQ, then its entropy increases by đQ/T. In this process an equal amount of heat flows out of the system and its entropy decreases by đQ/T. Hence d. S (universe) = 0. In a reversible process, the change in entropy of the universe is zero. 12

Tds Equations. (Study derivations and examples in textbook. ) 1 st Tds equation: 2 nd Tds equation: 3 rd Tds equation: One way to begin the derivations is as follows: First equation: start with s(T, v) Second equation: start with s(T, P) Third equation: start with s(P, v) Remember that in a reversible process d q=Tds 13

These equations follow from the first and second laws of thermodynamics and thus contain much of the content of thermodynamics. They are often a good starting point for working problems or obtaining other useful relationships. Some examples of the use of these equations are: (a) to find the heat transferred in a reversible process (Slide 19) (b) the entropy can be obtained by dividing by T and integrating. (c) equations express heat flow or entropy in terms of measurable properties, such as (d) can be used to determine the difference in the specific heat capacities at constant P and constant V (Slide 21) (e) can provide relationships between pairs of coordinates in a reversible adiabatic process ( ds=0 ) (Slides 18, 20) 14

Derivation of the 1 st Tds equation Consider đ Comparing (1) and (2) Since s is an exact differential: 15

= Placing in equation (2) 16

Helpful expansion: 17

Example: What is the change in temperature when a solid or liquid is compressed adiabatically and reversibly? Using the 1 st Td. S equation and remembering that for an adiabatic process, d. S=0 Assuming that the experimental quantities are approximately constant over the range of interest and integrating: In such a process the change in temperature is generally small, so If the volume decreases, the temperature must increase! 18

To obtain the change in temperature in terms of pressure, we could start with the 2 nd Td. S equation and go through a similar analysis. The result is (show): If the pressure increases, the temperature must increase! Example: How much energy is released during an reversible isothermal compression of a solid or liquid? We use the 2 nd Td. S equation and for an isothermal process, d. T=0 We make the approximations that are nearly constant. 19

Example: During a reversible, adiabatic compression, how are the volume and pressure changes related? Use the 3 rd Td. S equation and again d. S=0 Assuming constant specific heats and experimental quantities: (reversible adiabatic process) Of course, we already know that if the pressure is increased, the volume will decrease. The above expression permits a calculation of the change in the volume for a given change in the pressure. 20

EXAMPLE: Determination of Is this difference constant? If not, what does it depend upon? We equate the first two Tds equations. Brings in the two specific heats. Volume expansivity Isothermal compressibility 21

Solving for d. T But we can write Comparing gives This shows that always. is easy to determine experimentally, but is difficult If is measured, then can be obtained if the quantities on the right hand side have been measured. An example is given on the next slide. 22

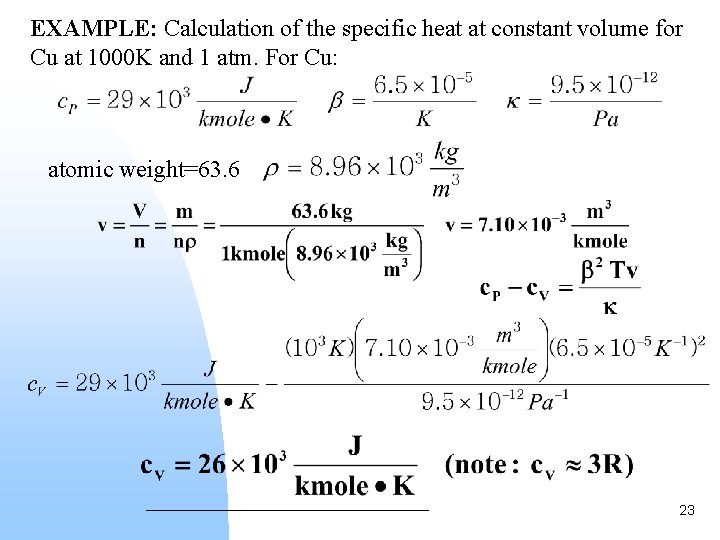
EXAMPLE: Calculation of the specific heat at constant volume for Cu at 1000 K and 1 atm. For Cu: atomic weight=63. 6 23

EXAMPLE: Consider a reversible adiabatic process, then ds=0 From the 3 rd Tds equation: giving: We define an adiabatic ( or isentropic) compressibility We can understand how this comes about. 24

An increase in pressure results in a decrease in the volume. Consider a small increase in pressure ΔP. For an isothermal process (heat will leave the system) there will be a certain decrease in volume (ΔV)T Now consider an isentropic process (no heat leaves the system) with the same increase in pressure. The increased pressure leads to an increase in temperature which tends to increase the volume. Hence, in this case, (ΔV)S will be less than (ΔV)T But and Hence The isentropic compressibility is smaller than the isothermal compressibility 25

Example: How much work is performed during a reversible, adiabatic compression of a solid or liquid? Starting with the definition of the isentropic compressibility: (reversible, adiabatic) Work is done on the system! 26

n Irreversible processes We defined entropy in terms of reversible processes. What about irreversible processes? Entropy is a state variable and change of entropy between any two equilibrium states is the same regardless of the process. Hence we can calculate S for any irreversible process between two equilibrium states by choosing any convenient path (reversible) between the same two states! Of course, regardless of the process, the change in entropy of the system must be the same, but the change in entropy of the universe will depend on the process. 27

As an example consider the following situation in which we have a large reservoir at temperature T 2 and a small body (system) at a lower temperature T 1. We let the system come into thermal equilibrium by means of some isobaric process, which is necessarily irreversible. body reservoir T 1 T 2 Q adiabatic walls 28

Now we imagine a reversible process, by which we bring about the change in T of the body through a whole series of reservoirs between T 1 and T 2, and keeping constant the pressure. In this manner the body passes through a large number of equilibrium states. For the reversible process, and using the second Tds equation and since d. P = 0 d. S = CP Upon integration S (body) = CP ln The heat absorbed is 29

The temperature of the reservoir remains constant and the heat flow out of the reservoir is -CP(T 2 -T 1). Hence, for the reservoir, regardless of whether T 2 > T 1 or T 1 > T 2. (Students: Let x = T 2/T 1 and examine the function). Hence S (universe) > 0. 30

In this example the decrease in entropy of the reservoir is less than the increase in entropy of the body In all real processes the entropy increases or, to put it in another way, entropy is created. The entropy of the universe is constantly increasing. It should be kept in mind that, for an irreversible process, đ and hence this formula cannot be used to calculate any entropy change that occurs. 31

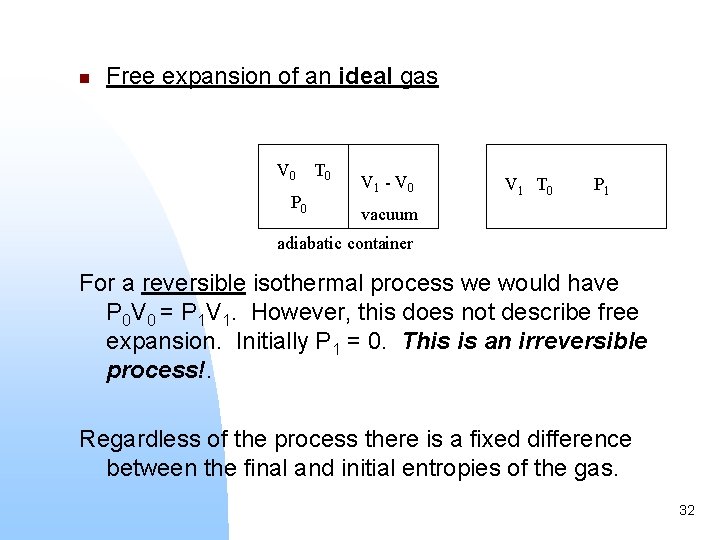
n Free expansion of an ideal gas V 0 P 0 T 0 V 1 - V 0 V 1 T 0 P 1 vacuum adiabatic container For a reversible isothermal process we would have P 0 V 0 = P 1 V 1. However, this does not describe free expansion. Initially P 1 = 0. This is an irreversible process!. Regardless of the process there is a fixed difference between the final and initial entropies of the gas. 32

We can calculate S by assuming a reversible isothermal expansion between the two equilibrium states. Because of the adiabatic walls, S (surroundings) = 0. (1 st Tds equation for an ideal gas) Even in this adiabatic process the entropy of the universe increases. Later we will provide some insight as to why this is so. The two processes, the free expansion and the reversible expansion, are completely different. What they have in common is that the initial and final states of the gas are the same. 33

In a reversible isothermal expansion, the work done by the ideal gas is W = n. RT 0 ln d. U = 0 Q=W S = n. Rln In a free expansion no work is done, but the change in entropy is as if work were done in a reversible, isothermal process between the same endpoints. To Summarize: reversible process irreversible process S (universe) = 0 S (universe) > 0 If the entropy of the universe increases in some process, we know 34 that it is irreversible.

Entropy change for a liquid or a solid An approximate equation of state for a liquid or solid is 2 nd Tds equation: Since and since the volume does not change drastically for a liquid or solid, we write: Substituting into the Tds equation gives: Integration gives If T increases, s increases. If P increases, s decreases. 35

Comments: 2 nd Law: energy tends to disperse. Natural processes accompany the dispersal of energy High quality energy is undispersed energy (energy in a lump of coal) or stored in coherent motion (flow of water) A local reduction of entropy is possible (such as cooling something below surroundings). 36

Example: Express in standard form. Evaluate this partial for an ideal gas. (Not obvious how to start. ) (start with 1 st law) But writing s(T, P) and comparing 37

Since ds is an exact differential: 38

( measurable quantities) For an ideal gas Using these expression in the expression at the top: 39