Entropy Entropy of Mixing ideal gas Container divided









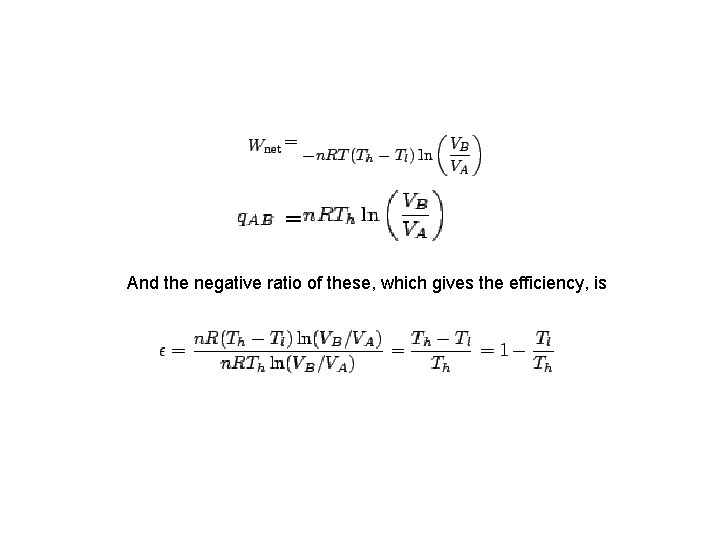





- Slides: 16

Entropy

Entropy of Mixing (ideal gas) • Container divided into two compartments. In one compartment we have n 1 moles of an ideal gas, gas 1, at pressure, p and temperature, T. • In the other compartment we have n 2 moles of another ideal gas, gas 2, at the same p and T. • If we remove the partition the gases will begin to diffuse into each other and the system will eventually reach the state where both gases are uniformly distributed throughout the container. • This is clearly an irreversibly process so that we would expect that the entropy would increase.

Imagine that we can devise a process that will expand one gas reversibly and isothermally, but leave the other gas undisturbed. We know how to calculate the change in entropy for the reversible isothermal expansion of an ideal gas. Recall that d. U = 0 for the isothermal expansion of an ideal gas. Then, So, for an ideal gas. So, for gas number 1 in our fictitious isothermal expansion we have,

and for gas number 2, The total entropy change is the sum of these two individual entropy changes, To obtain the usual form factor the R out and invert the argument of the logarithms,

where X 1 is the mole fraction of component 1. There is an equivalent expression for the argument of the second logarithm. The entropy of mixing becomes, To obtain the standard form write the total number of moles n 1 + n 2 as n and multiply and divide by n. The result is This equation can easily be extended to more than two gases,

The composition of dry air is approximately 78% N 2, 21% O 2, and 1% Ar by volume (which is the same as mole percent). What is the molar entropy of mixing of air?

Irreversible, Isothermal Expansion of an Ideal gas If we compare this to the work done by the gas in a reversible expansion, where the system is always in equilibrium with its surroundings, i. e. , , then the reversible work is Thus, since for the irreversible process, it follows that

However, the internal energy change , being a state function, will be the same for both the irreversible and reversible processes: Since , it follows that For an isothermal process Thus, or, in general,

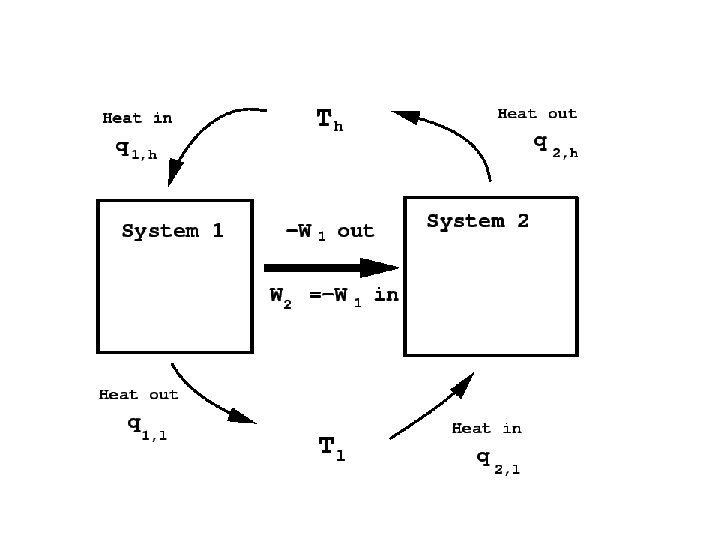
Efficiency of the Carnot engine • The efficiency of a device is defined to be the net work it can produce per unit of heat taken in: • Thus, if all of the heat taken in is converted to useful work with no discharge of waste heat, then the device is 100% efficient. We will now show that such a case is not possible. • For the Carnot cycle, in which a system containing an ideal gas undergoes reversible transformations around the cycle.
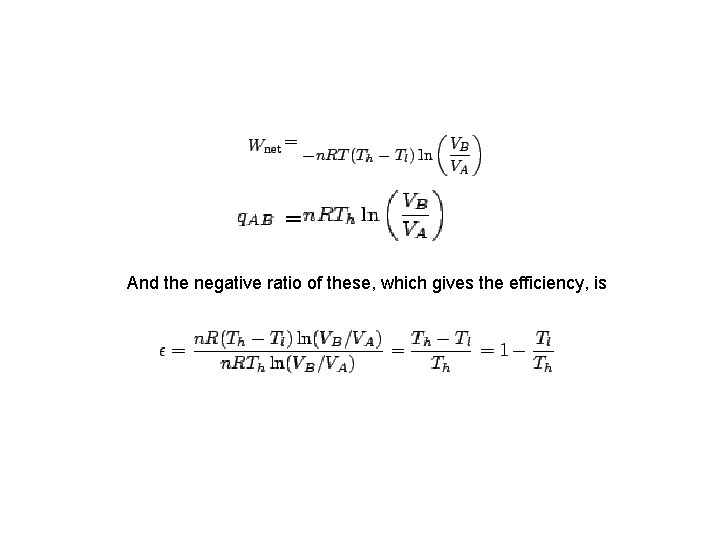
And the negative ratio of these, which gives the efficiency, is

• For Carnot engine, 100 % efficiency can only be achieve when Tl = 0 or Th = ∞. • The larger the temperature difference, the greater will be the efficiency of the device. • The difficulty with large temperature differences, in general, is that they are difficult to make. • It is also difficult to find materials that can withstand both extremely high AND extremely low temperatures.




