ENGG 2013 Unit 24 Linear DE and Applications
























![Modeling • • Consider a short time interval [t, t+ t] C 1 = Modeling • • Consider a short time interval [t, t+ t] C 1 =](https://slidetodoc.com/presentation_image_h/de8b14bb319ac27ecf7adb5bac05cfe9/image-27.jpg)







- Slides: 40

ENGG 2013 Unit 24 Linear DE and Applications Apr, 2011.

Outline • Method of separating variable • Method of integrating factor • System of linear and first-order differential equations – Graphical method using phase plane kshum 2

Nomenclatures • “First-order”: only the first derivative is involved. • “Autonomous”: the independent variable does not appear in the DE • “Linear”: – “Homogeneous” – “Non-homogeneous” c(t) not identically zero kshum 3

Separable DE • “Separable”: A first-order DE is called separable if it can be written in the following form • Examples – x’ = cos(t) – x’ = x+1 – x’ = t 2 sin(x) – t x’ = x 2– 1 – All linear homogeneous DE kshum 4

SEPARABLE DE AND METHOD OF SEPARATING VARIABLES kshum 5

How to solve separable DE • Write x’= f(x) g(t) as . • Separate variable x and t (move all “x” to the LHS and all “t” to the RHS) • Integrate both sides kshum 6

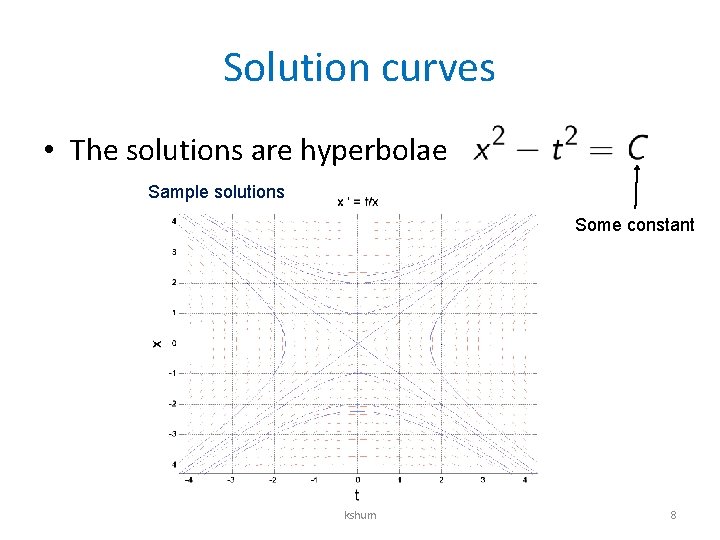
Example Solve (1) Write the DE as (2) Separate the variables (3) Integrate both sides General solution to x’=t/x kshum 7

Solution curves • The solutions are hyperbolae Sample solutions Some constant kshum 8

Example: Newton’s law of cooling • Suppose that the room temperature is Tr = 24 degree Celsius. The temperature of a can of coffee is 15 o. C at T=0 and rises to 16 o. C after one minute. – T(0) = 15, T(1) = 16. • Find the temperature after 10 minutes Proportionality constant kshum 9

LINEAR NON-HOMOGENEOUS DE METHOD OF INTEGRATING FACTOR kshum 10

Example: RC in series • Physical laws – Voltage drop across resistor = VR(t) = R I(t) – Voltage drop across inductor = C VC(t) = Q(t) Charge From Kirchoff voltage law VC(t) + VR(t) = sin( t) Linear non-homogeneous kshum 11

Linear DE in standard form • Linear equation has the following form • By dividing both sides by p(t), we can write the differential equation in standard form kshum 12

Product rule of differentiation • Idea: Given a DE in standard form Multiply both sides by some function u(t) so that the product rule can be applied. kshum 13

Illustrations 1. Solve the initial value problem 2. Find the general solution to kshum 14

Example: Mixing problem Water tank 1000 L Initial Caesium concentration = 1 Bq/L • In-flow of water: 10 L per minute • Out-flow of water: 10 L per minute • In-flowing water contains Caesium with concentration 5 Bq/L • Describe the concentration of Ce in the water tank as a function of time. kshum 15

http: //en. wikipedia. org/wiki/Henri_Becquerel Henri Becquerel • French physicist • Dec 1852 ~ Aug 1908 • Nobel prize laureate of Physics in 1903 (together with Marie Curie and Pierre Curie) for the discovery of radioactivity. • Bq is the SI unit for radioactivity – Defined as the number of nucleus decays per second. kshum 16

Back to the RC example • Write it in standard form • Multiply by an unknown function u(t) kshum 17

Integrating factor • Is there any function u(t) such that u’(t) = u(t)/RC ? • Choose u(t) = exp(t/RC) kshum 18

Now we can integrate Use a standard fact from calculus kshum 19

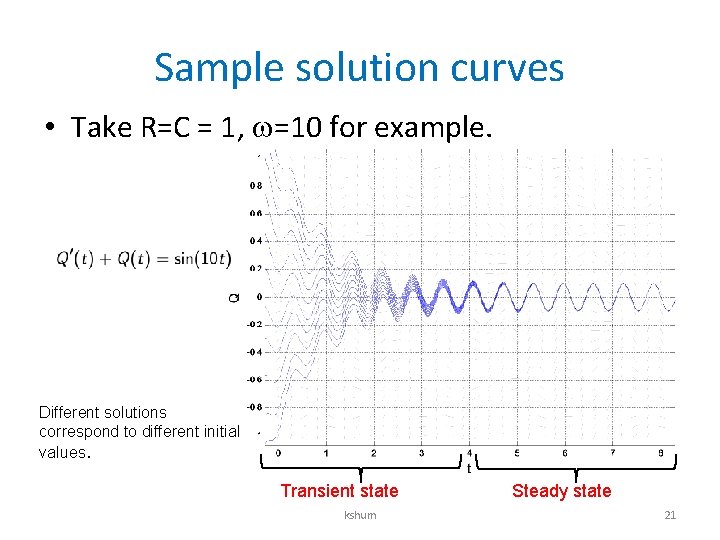
Solution to RC in series • General solution • If it is known that Q(0) = 0, then Steady-state solution kshum approaches zero as t 20

Sample solution curves • Take R=C = 1, =10 for example. Different solutions correspond to different initial values. Transient state kshum Steady state 21

SYSTEM OF DIFFERENTIAL EQUATIONS kshum 22

Interaction between components • If we have two or more objects, each and they interact with each other, we need a system of differential equations. • Metronomes synchronization – http: //www. youtube. com/watch? v=yysnk. Y 4 WHy. M • Double pendulum – http: //www. youtube. com/watch? v=p. YPRnx. S 6 u. Aw kshum 23

General form of a system of linear differential equation • System variables: x 1(t), x 2(t), …, xn(t). • A system of DE Some functions kshum 24

System of linear constant-coeff. differential equations • System variables: x 1(t), x 2(t), x 3(t). • Constant-coefficient linear DE – aij are constants, – g 1(t), g 2(t) and g 3(t) are some function of t. • Matrix form: kshum 25

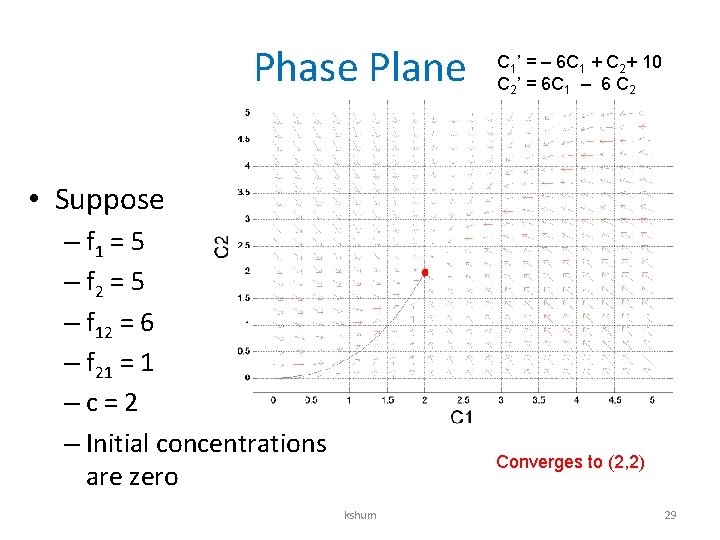
Application 1: Mixing Water tank 1 f 12 Water tank 2 f 2 Volume = V 2 m 3 Volume = V 1 m 3 Concentration = C 1(t) f 21 Concentration = C 2(t) • C 1(t) and C 2(t) are concentrations of a substance, e. g. salt, in tank 1 and 2. • Given – – – Initial concentrations C 1(0) = a, C 1(0) = b. In-low to tank 1 = f 1 m 3/s, with concentration c. Flow from tank 1 to tank 2 = f 12 m 3/s Flow from tank 2 to tank 1 = f 21 m 3/s Out-flow from tank 2 = f 2 m 3/s • Objective: Find C 1(t) and C 2(t). kshum 26
![Modeling Consider a short time interval t t t C 1 Modeling • • Consider a short time interval [t, t+ t] C 1 =](https://slidetodoc.com/presentation_image_h/de8b14bb319ac27ecf7adb5bac05cfe9/image-27.jpg)
Modeling • • Consider a short time interval [t, t+ t] C 1 = C 1(t+ t)–C 1(t) = cf 1 t + f 21 C 2 t – f 12 C 1 t C 2 = C 2(t+ t)–C 2(t) = f 12 C 1 t – f 21 C 2 t – f 2 C 2 t Take t 0, we have C 1’ = – f 12 C 1 + f 21 C 2+ cf 1 C 2’ = f 12 C 1 – (f 21+ f 2) C 2 kshum 27

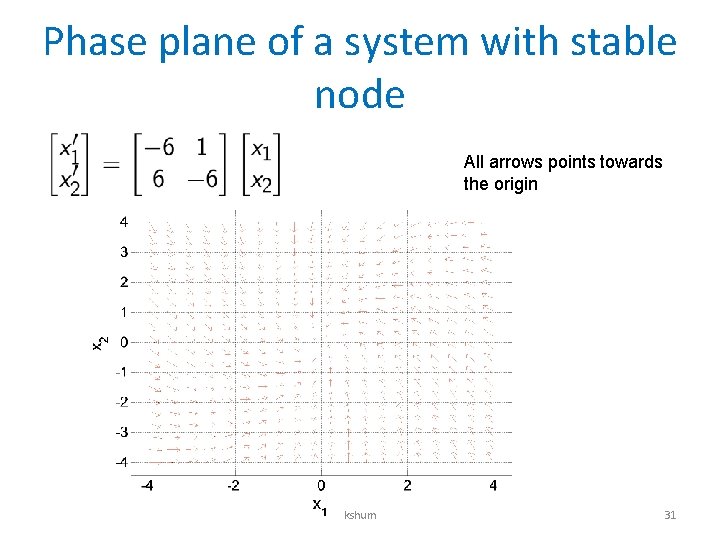
Graphical method • For autonomous system, • we can plot the phase plane (aka phase portrait) to understand the system qualitatively. • Select a grid of points, and draw an arrow for each point. The direction of each arrow is kshum 28

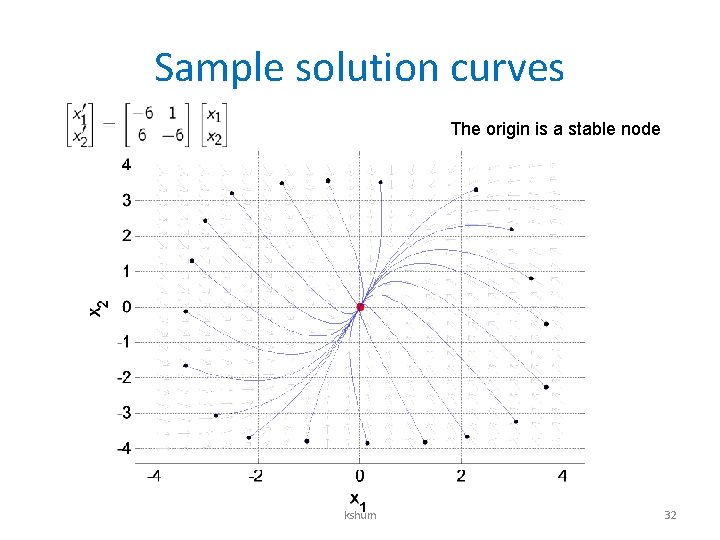
Phase Plane C 1’ = – 6 C 1 + C 2+ 10 C 2’ = 6 C 1 – 6 C 2 • Suppose – f 1 = 5 – f 2 = 5 – f 12 = 6 – f 21 = 1 –c=2 – Initial concentrations are zero Converges to (2, 2) kshum 29

Convergence C 1’ = – 6 C 1 + C 2+ 10 C 2’ = 6 C 1 – 6 C 2 • (C 1, C 2)=(2, 2) is a critical point. – C 1’ and C 2’ are both zero when C 1= C 2=2. • The analyze the stability of critical point, we usually make a change of coordinates and move the critical point to the origin. • Let x 1 = C 1– 2, x 2 = C 2– 2. x 1’ = – 6 x 1 + x 2’ = 6 x 1 – 6 x 2 kshum 30

Phase plane of a system with stable node All arrows points towards the origin kshum 31

Sample solution curves The origin is a stable node kshum 32

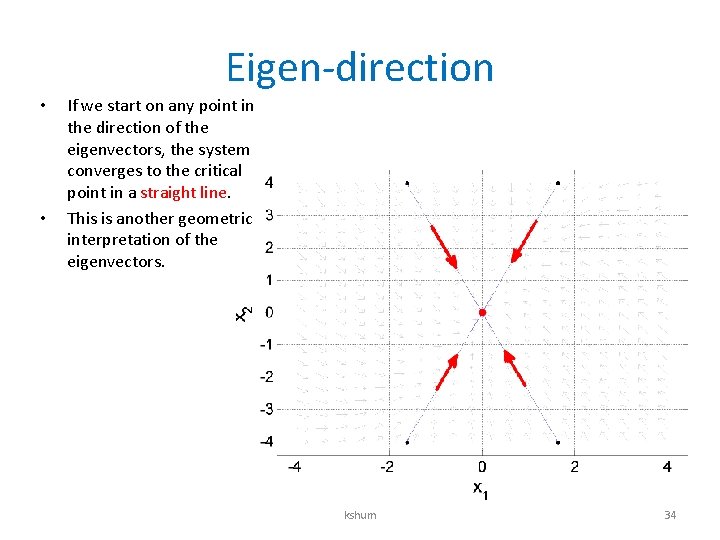
Theoretical explanation for convergence • The eigenvalues of the coefficient matrix are negative. Indeed, they are equal to – 3. 5505 and – 8. 4495. • The corresponding eigenvectors are [0. 3780 0. 9258] and [– 0. 3780 0. 9258] kshum 33

Eigen-direction • • If we start on any point in the direction of the eigenvectors, the system converges to the critical point in a straight line. This is another geometric interpretation of the eigenvectors. kshum 34

Application 2: RLC mesh circuit • Suppose that the initial charge at the capacity is Q 0. • Describe the currents in the two loops after the switch is closed. i 1(t) i 2(t) Physical Laws • Resistor: V=R i • Inductor: V=L i’ • Capacitor: V=Q/C • KVL, KCL Homework exercise kshum 35

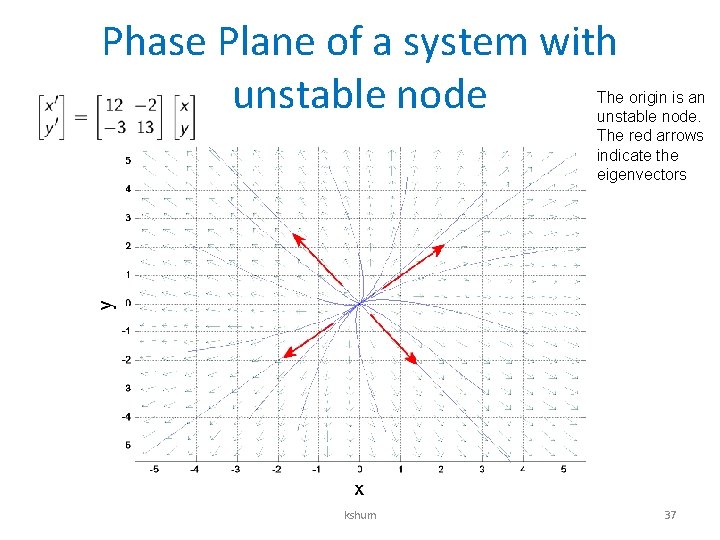
An expanding system • Both eigenvalues are positive. kshum 36

Phase Plane of a system with unstable node The origin is an unstable node. The red arrows indicate the eigenvectors kshum 37

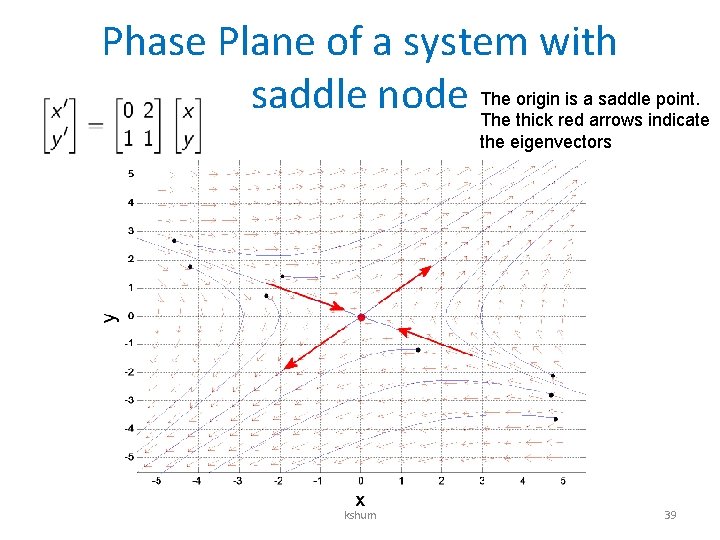
A system with saddle point • One eigenvalue is positive, and another eigenvalue is negative kshum 38

Phase Plane of a system with origin is a saddle point. saddle node The thick red arrows indicate the eigenvectors kshum 39

Conclusion The convergence and stability of a system of linear equations is intimately related to the signs of eigenvalues. kshum 40
 Engg2780
Engg2780 Civil engg drawing house planning
Civil engg drawing house planning Engg 1100
Engg 1100 Engg 1100
Engg 1100 Diagonalizable matrix
Diagonalizable matrix Systems of linear equations real world applications
Systems of linear equations real world applications Chapter 8 linear programming applications solutions
Chapter 8 linear programming applications solutions Non linear op amp applications
Non linear op amp applications Unit 6 review questions
Unit 6 review questions Simple and multiple linear regression
Simple and multiple linear regression Linear texts examples
Linear texts examples Non-linear plot definition
Non-linear plot definition Difference between linear and nonlinear pipeline processors
Difference between linear and nonlinear pipeline processors A multimedia project is identified as non-linear when
A multimedia project is identified as non-linear when Linear momentum and linear impulse
Linear momentum and linear impulse Persamaan linear simultan
Persamaan linear simultan Linear grammar
Linear grammar Difference between linear and nonlinear
Difference between linear and nonlinear Simultaneous nonlinear equations
Simultaneous nonlinear equations Elements of computer
Elements of computer Contoh soal metode biseksi dan penyelesaiannya
Contoh soal metode biseksi dan penyelesaiannya Contoh soal persamaan non linear dengan metode biseksi
Contoh soal persamaan non linear dengan metode biseksi Perbedaan fungsi linier dan non linier
Perbedaan fungsi linier dan non linier Contoh fungsi non linear
Contoh fungsi non linear Linearly independent
Linearly independent Linear algebra 1
Linear algebra 1 Cara dwi koordinat
Cara dwi koordinat Identify linear and nonlinear equations
Identify linear and nonlinear equations Nonlinear table
Nonlinear table Linear and nonlinear editing
Linear and nonlinear editing Right linear grammar to left linear grammar
Right linear grammar to left linear grammar Textos com falas
Textos com falas Reasoning with linear equations
Reasoning with linear equations Polynomials linear factors and zeros
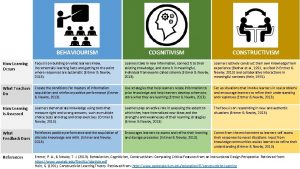
Polynomials linear factors and zeros Constructivism vs behaviorism vs cognitivism
Constructivism vs behaviorism vs cognitivism Coso cube 2013
Coso cube 2013 Application of heat transfer
Application of heat transfer Image sets
Image sets Unit 4 linear equations
Unit 4 linear equations Unit 1 lesson 3 review of linear systems
Unit 1 lesson 3 review of linear systems Unit 2 linear functions homework 2
Unit 2 linear functions homework 2