Unit 2 Week 5 Reasoning with Linear Equations






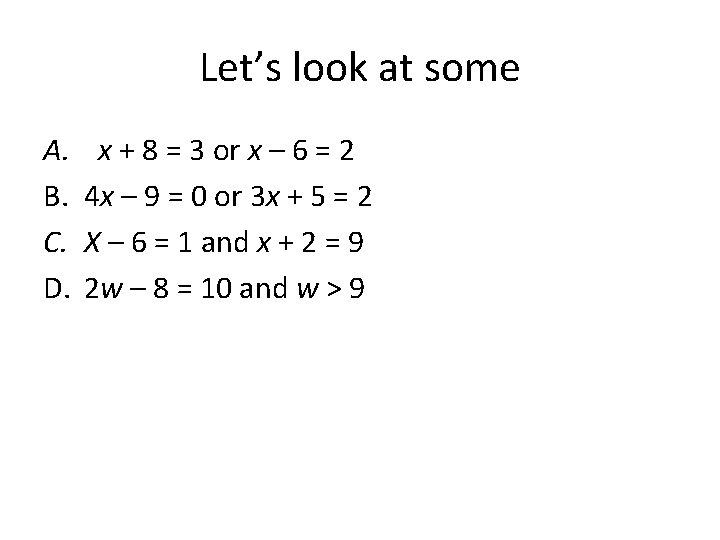






- Slides: 13

Unit 2 – Week 5 Reasoning with Linear Equations and Inequalities Lesson 3 Students describe the solution set of two equations or inequalities joined by either “and” or “or” and graph the solution set on a number line. Lesson 15 Story of Functions

Standards • A. CED. 1 – Create inequalities in one variable and use them to solve problems. (integer inputs only) • A. CED. 3 – Represent constraints by inequalities and interpret data points as possible or not possible solutions. • A. REI. 3 – Solve linear equations in one variable including equations with coefficients represented by letters.

Essential Questions • What is a compound sentence? • What is a declarative sentence? • Does the word “and” mean the same thing in a compound mathematical sentence as it does in an English sentence? • What is a compound math sentence?

Read, Write, Draw, Solve • Determine whether each claim given below is true or false. A. B. C. D. E. F. Right now, I am in math class and English class. Right now, I am in math class or English class. 3+5=8 and 5<7 -1. 10+2≠ 12 and 8 -3>0. 3<5+4 or 6+4=9. 16 -20>1 or 5. 5+4. 5=11 • These are all examples of declarative compound sentences. G. H. When the two declarations in the sentences above were separated by “and, ” what had to be true to make the statement true? When the two declarations in the sentences above were separated by “or, ” what had to be true to make the statement true?

Discussion - Activator • How does the word “and” mean the same thing in an English sentence and a math sentence?

Discussion • How does the word “or” mean a similar thing in a compound mathematical sentence as it does in an English sentence?
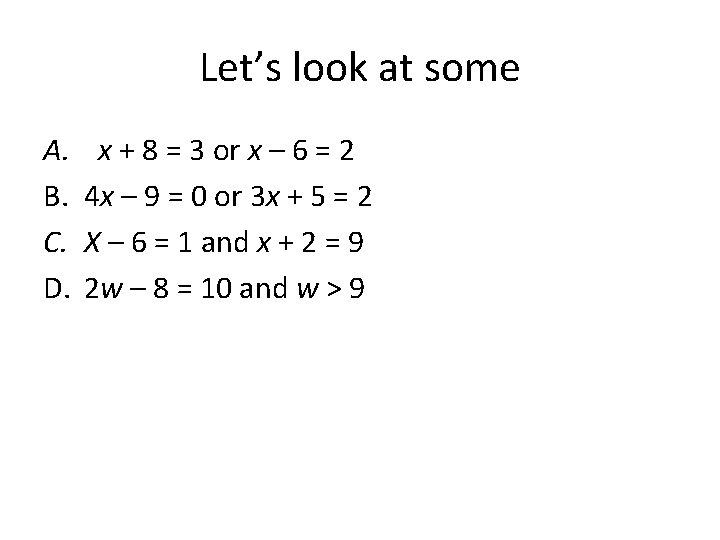
Let’s look at some A. B. C. D. x + 8 = 3 or x – 6 = 2 4 x – 9 = 0 or 3 x + 5 = 2 X – 6 = 1 and x + 2 = 9 2 w – 8 = 10 and w > 9

Exercise 2 Questions • In order for the compound sentence x > -1 and x < 3 to be true, what has to be true about x? • Where do the solutions lie on the graph? • What are some solutions that are possible for this compound inequality? • How many solutions are there to this compound inequality?

Ways to write you solution set • X can be any number that is between -1 and 3 • -1 < x < 3 • Or displayed on the number line

Exercise 3 Questions • In order for the compound sentence x < -4 or x > 0 to be true, what has to be true about x? • Where do the solutions lie on the graph? • What are some solutions that are possible for this compound inequality? • Would it be acceptable to write this compound sentence as follows: 0 < x < -4? Why or why not? • How many solutions are there to this compound inequality?

Ways to write you solution set • Sentence • Abbreviation • Number Line

Continue with Practice

Summarizer Consider each of the following compound sentence. x < 1 and x > -1 x < 1 or x > -1 Does changing the word from ‘and’ to ‘or’ change the solution set? Explain why. Create a number line graph for each compound sentence to support your reasoning.
 Unit 2 reasoning with linear equations and inequalities
Unit 2 reasoning with linear equations and inequalities Unit 2 lesson 4 solving equations
Unit 2 lesson 4 solving equations Penyelesaian persamaan simultan
Penyelesaian persamaan simultan Difference between linear and non linear equation
Difference between linear and non linear equation Simultaneous nonlinear equations
Simultaneous nonlinear equations Week by week plans for documenting children's development
Week by week plans for documenting children's development Definition of inductive method
Definition of inductive method Deductive reasoning process
Deductive reasoning process Deductive logic definition
Deductive logic definition Inductive reasoning vs deductive reasoning
Inductive reasoning vs deductive reasoning Every quiz has been easy. therefore the quiz will be easy
Every quiz has been easy. therefore the quiz will be easy Patterns and inductive reasoning
Patterns and inductive reasoning Inductive reasoning and deductive reasoning
Inductive reasoning and deductive reasoning Unit 4 linear equations
Unit 4 linear equations
























