2 2 Linear Equations Linear Equations Linear Function













- Slides: 31

2. 2 Linear Equations

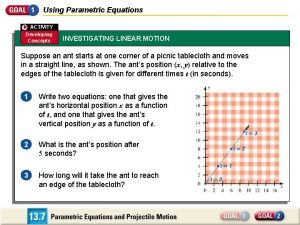
Linear Equations Linear Function: Functions whose graph is a line. Dependent Variable: y is a dependent variable of x because y is the output of x. Independent Variable: x is an independent variable because x is your input values.

Slope Dude http: //www. teachertube. com/view. Video. php? title=Slope_Dude &video_id=125151

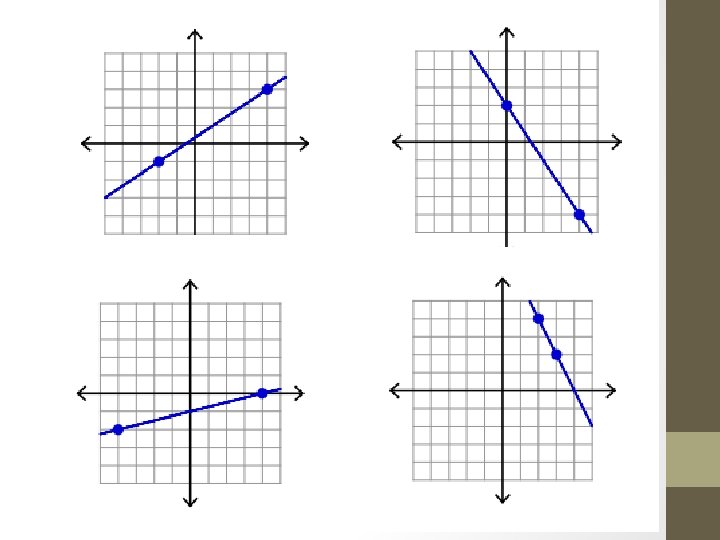
• Slope is the rate of vertical change to the horizontal change of a line. • Slope can be expressed as • The formula for Slope is Where a line, and are two points on

When finding slope from a graph use Pick two points on the line. Starting with the left most point, count rise and run When counting rise: Up is positive rise Down is negative rise When counting run: Right is positive run Left is negative run


When finding slope from two points use the formula

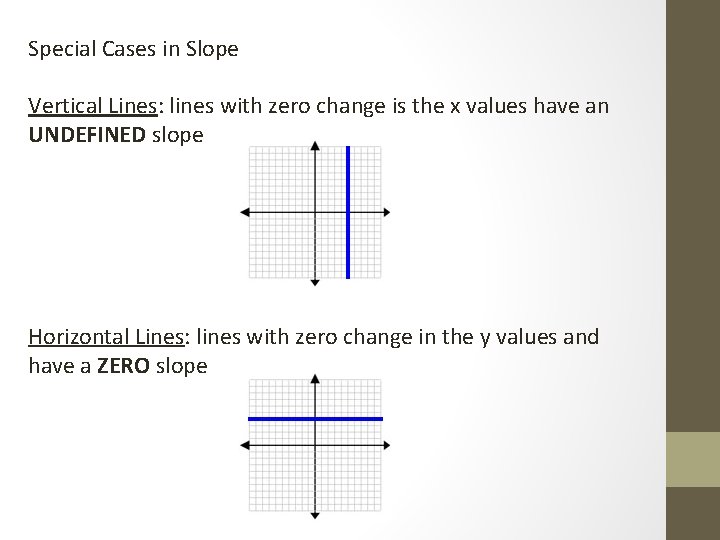
Special Cases in Slope Vertical Lines: lines with zero change is the x values have an UNDEFINED slope Horizontal Lines: lines with zero change in the y values and have a ZERO slope

slope-intercept form: • x and y are our variables • m is our slope • b is our y-intercept or where the line crosses the yaxis y-intercept RUN R I S E Slope

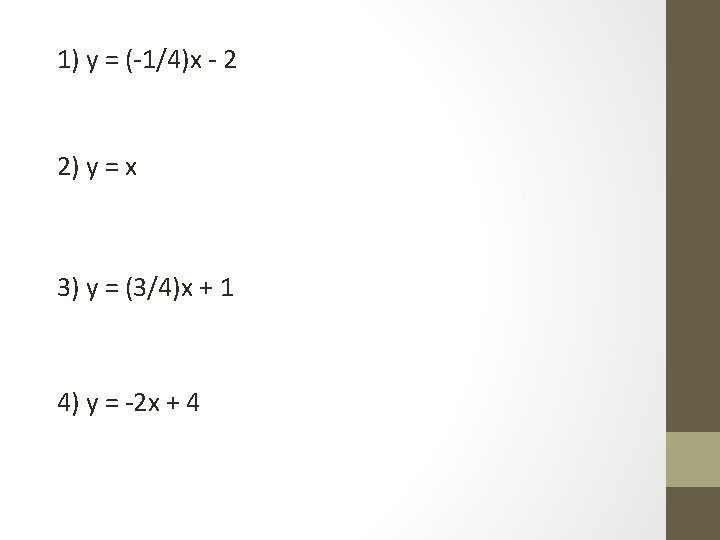
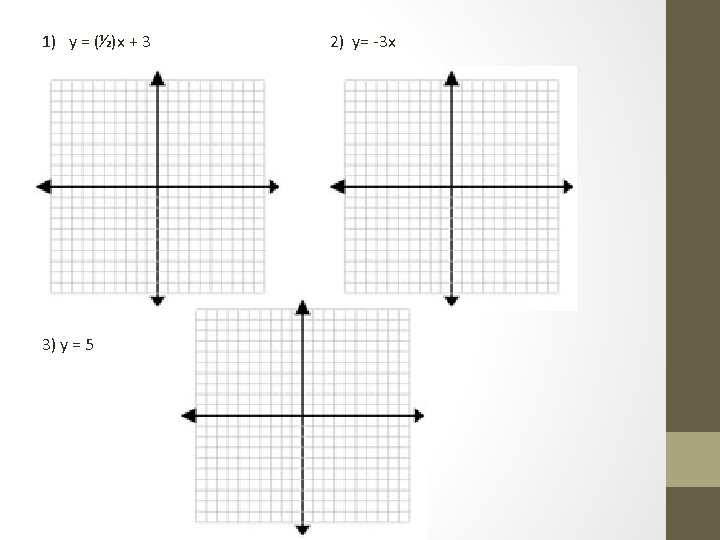
1) y = (-1/4)x - 2 2) y = x 3) y = (3/4)x + 1 4) y = -2 x + 4

Standard Form: Where A, B, and C are coefficients, and x and y are our variables. y-intercept (C/B) is our y-intercept (C/A) is our x-intercept

1) x – 3 y = 6 3) 5 x – 2 y =10 2) 2 x + y =4
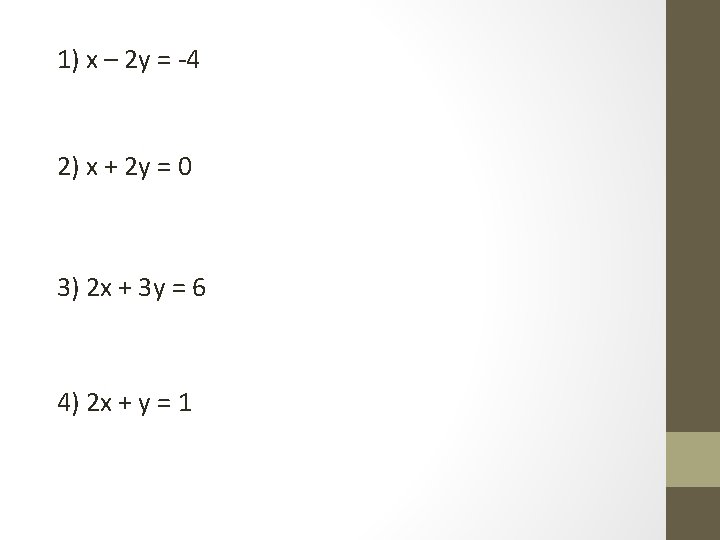
1) x – 2 y = -4 2) x + 2 y = 0 3) 2 x + 3 y = 6 4) 2 x + y = 1

Point-Slope Form: Another form of a linear equation is the point-slope form. This form is mainly used for when the yintercept is not clearly shown on the graph • Where x and y are our variables • m is the slope • And is any point on the line.

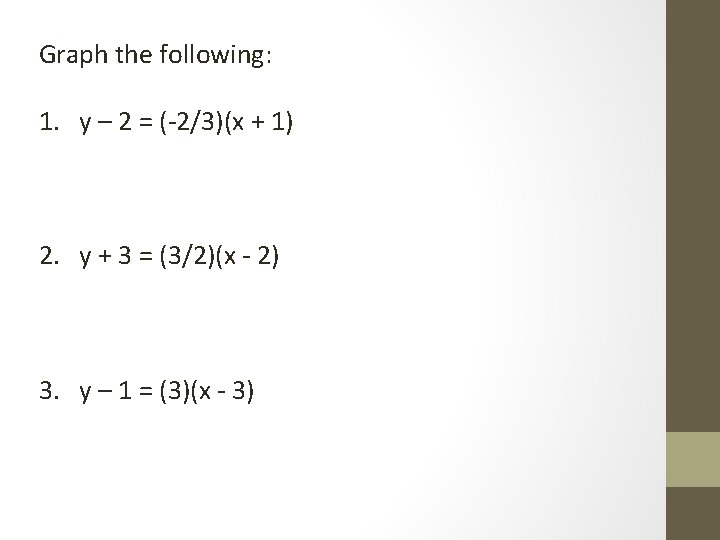
Graph the following: 1. y – 2 = (-2/3)(x + 1) 2. y + 3 = (3/2)(x - 2) 3. y – 1 = (3)(x - 3)

Writing Linear Equations

slope-Intercept Form: • Y and X are our variables • m = slope • b is our y-intercept, or where the line crosses the y-axis

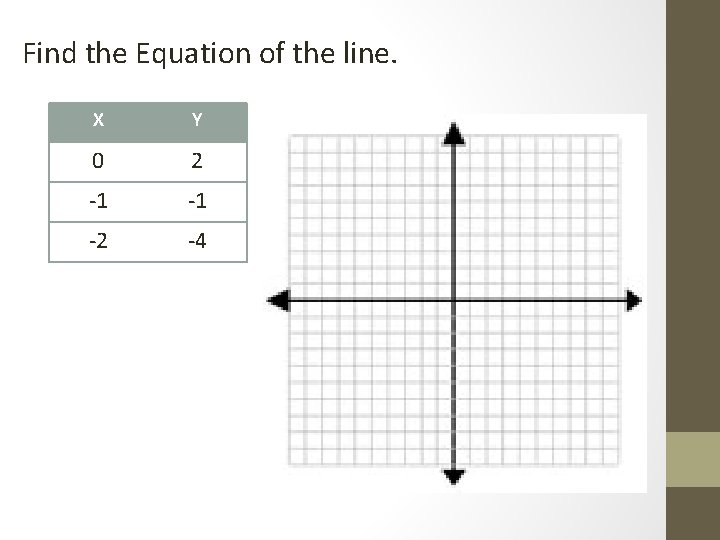
Find the Equation of the line. X Y 0 2 -1 -1 -2 -4

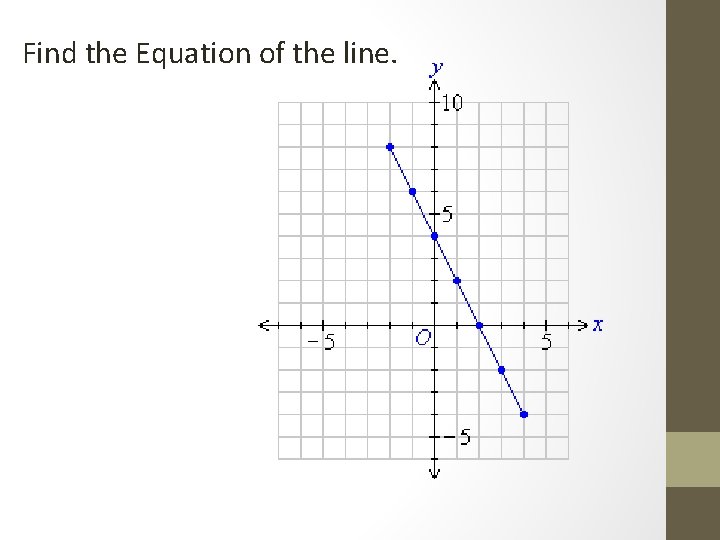
Find the Equation of the line.

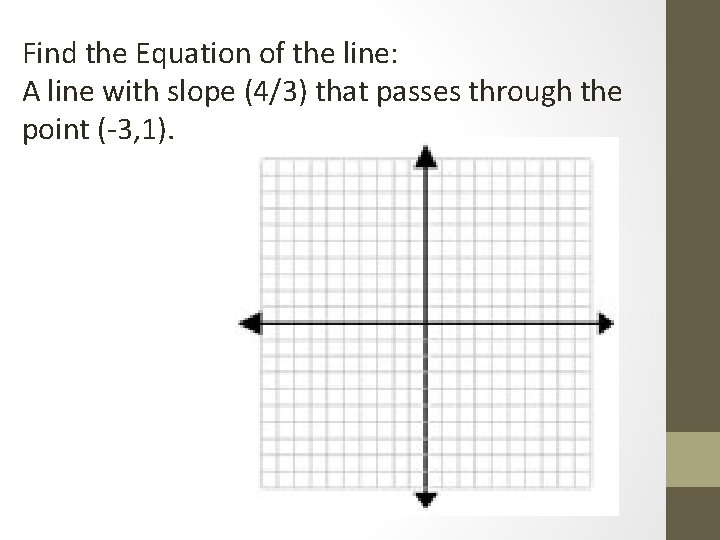
Find the Equation of the line: A line with slope (4/3) that passes through the point (-3, 1).

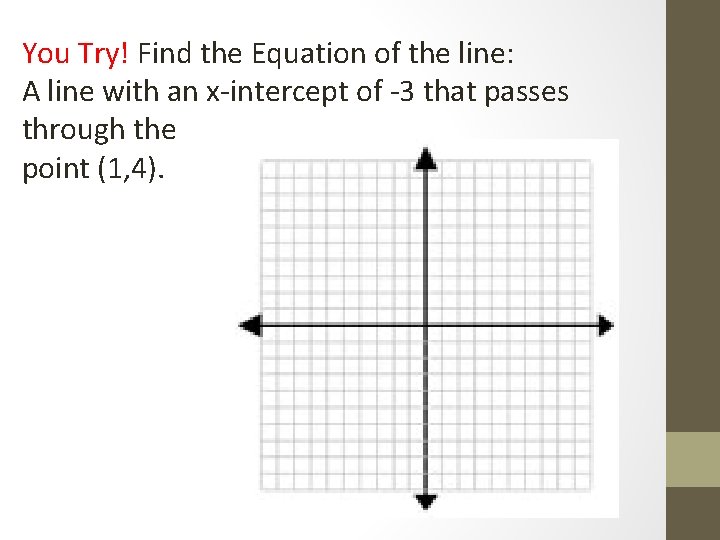
You Try! Find the Equation of the line: A line with an x-intercept of -3 that passes through the point (1, 4).

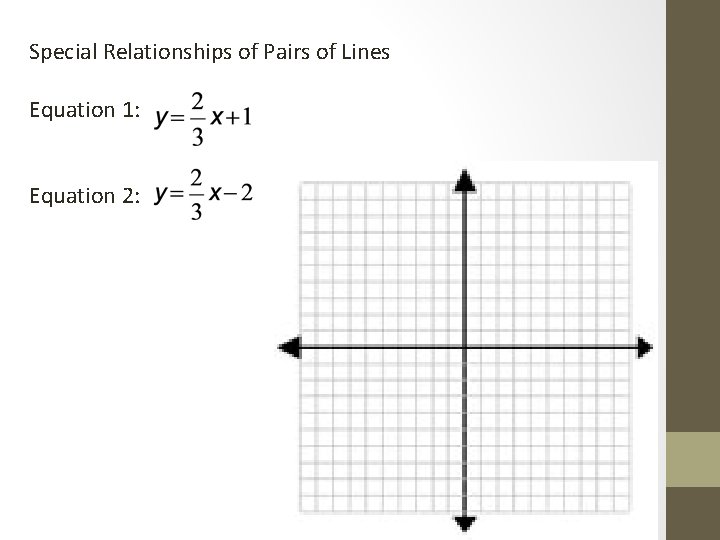
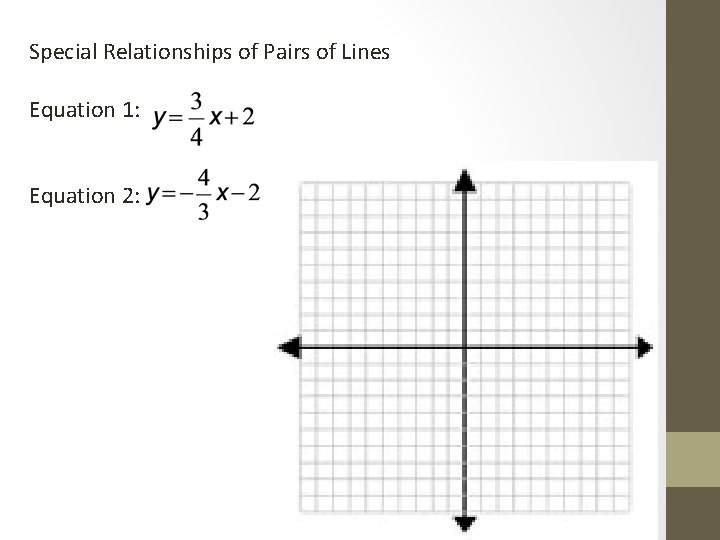
Special Relationships of Pairs of Lines Equation 1: Equation 2:

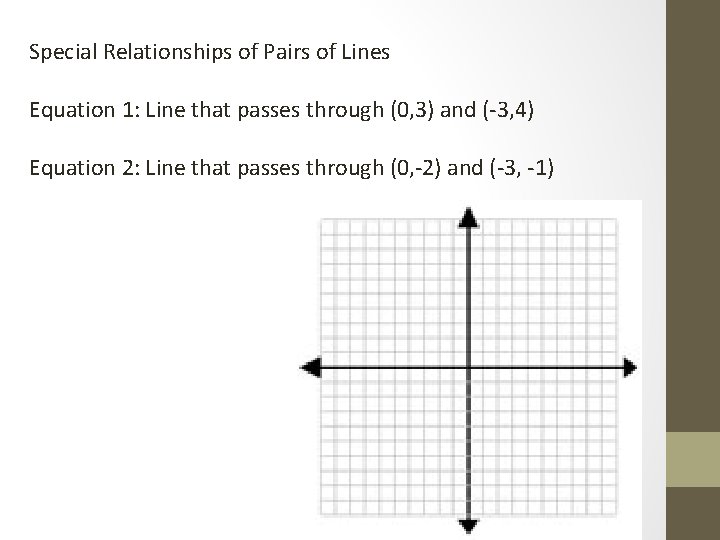
Special Relationships of Pairs of Lines Equation 1: Line that passes through (0, 3) and (-3, 4) Equation 2: Line that passes through (0, -2) and (-3, -1)

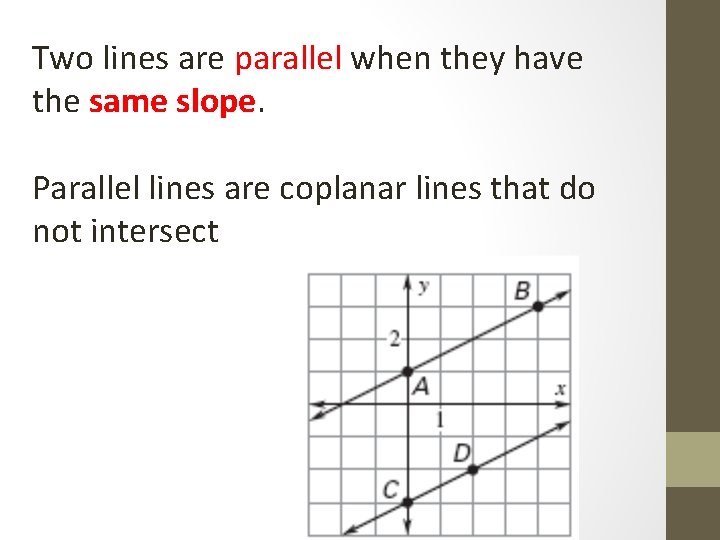
Two lines are parallel when they have the same slope. Parallel lines are coplanar lines that do not intersect

Determine if these pairs of lines are parallel. 1. y = (-1/4)x + 2 and y = (-1/2)x + 2 2. y = 2 x + 3 and y – 2 = 2(x + 1) 3. 2 x + 4 y = 8 and y = (-1/2)x – 2 4. y – 1 = (1/5)(x – 0) and 1 x – 6 y = 6

Special Relationships of Pairs of Lines Equation 1: Equation 2:

Special Relationships of Pairs of Lines Equation 1: Line that passes through (0, -1) and (4, -2) Equation 2: Line that passes through (0, -4) and (1, 0)

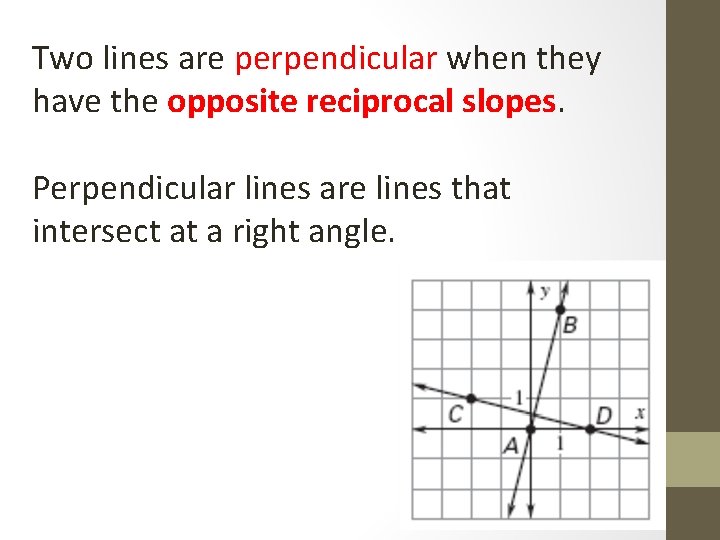
Two lines are perpendicular when they have the opposite reciprocal slopes. Perpendicular lines are lines that intersect at a right angle.

Determine if these pairs of lines are perpendicular. 1. y = (-2/3)x + 2 and y = (3/2)x + 1 2. y = 2 x + 4 and y – 2 = (1/2)(x + 1) 3. 4 x – 2 y = 8 and y = (-1/2)x – 2 4. y – 1 = (1/5)(x – 1) and 1 x – 6 y = 6
 Quadratic simultaneous equations
Quadratic simultaneous equations Difference between linear and non linear equations
Difference between linear and non linear equations Simultaneous nonlinear equations
Simultaneous nonlinear equations Linear vs nonlinear chart
Linear vs nonlinear chart Parent function notes
Parent function notes 9-3 polar and rectangular forms of equations
9-3 polar and rectangular forms of equations Translate word equations to chemical equations
Translate word equations to chemical equations Parents functions
Parents functions How to solve parametric equations
How to solve parametric equations Unit 4 writing linear equations
Unit 4 writing linear equations Reasoning with linear equations
Reasoning with linear equations Systems of linear equations word problems
Systems of linear equations word problems Vector form
Vector form System of linear equations with two variables
System of linear equations with two variables Standard form equation
Standard form equation How to do gauss elimination method
How to do gauss elimination method Solving systems of equations
Solving systems of equations Simultaneous linear equations problems
Simultaneous linear equations problems Solving linear equations calculator
Solving linear equations calculator Linear equation solver with steps
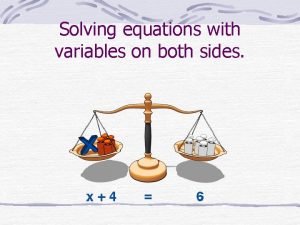
Linear equation solver with steps Solving linear equations with variables on both sides
Solving linear equations with variables on both sides Steps to solving equations with variables on both sides
Steps to solving equations with variables on both sides Solving linear equations fractions
Solving linear equations fractions Angular motion equations
Angular motion equations How to write an exponential function from a table
How to write an exponential function from a table Systems of linear equations real world applications
Systems of linear equations real world applications Different forms of linear equations
Different forms of linear equations Solving linear equations: variable on one side
Solving linear equations: variable on one side Forming equations worksheet
Forming equations worksheet Learning objectives of linear equations in one variable
Learning objectives of linear equations in one variable Core focus on linear equations
Core focus on linear equations Linear equations jeopardy
Linear equations jeopardy