3 2 Graphing Linear Equations Linear Equations Linear

§ 3. 2 Graphing Linear Equations

Linear Equations Linear Equation in Two Variables A linear equation in two variables is an equation that can be written in the form Ax + By = C where A, B, and C are real numbers and A and B are not both 0. The graph of a linear equation in two variables is a straight line. The form Ax + By = C is called standard form. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 2

Graphing Linear Equations Example: Graph the linear equation 2 x – y = – 4. We find two ordered pair solutions (and a third solution as a check on our computations) by choosing a value for one of the variables, x or y, then solving for the other variable. We plot the solution points, then draw the line containing the 3 points. Continued. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 3

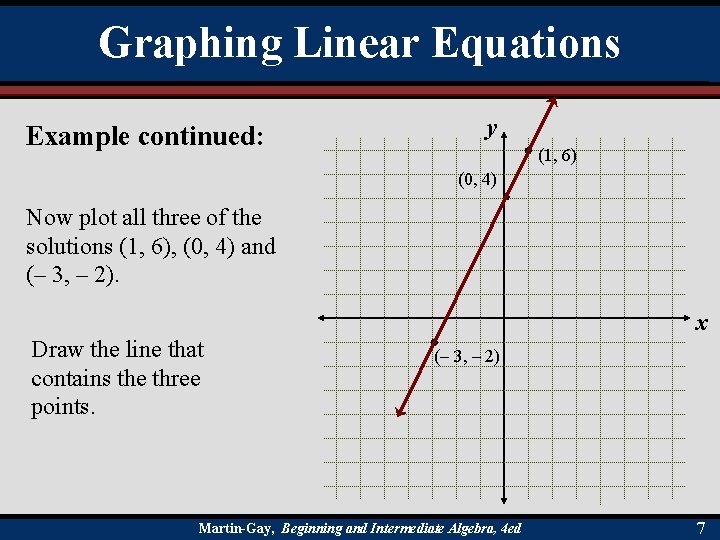
Graphing Linear Equations Example continued: Graph the linear equation 2 x – y = – 4. Let x = 1. 2(1) – y = – 4 2–y=– 4– 2=– 6 y=6 Replace x with 1. Simplify the left side. Subtract 2 from both sides. Multiply both sides by – 1. One solution to the equation is (1, 6). Continued. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 4

Graphing Linear Equations Example continued: Graph the linear equation 2 x – y = – 4. For the second solution, let y = 4. 2 x – 4 = – 4 2 x = – 4 + 4 2 x = 0 x=0 Replace y with 4. Add 4 to both sides. Simplify the right side. Divide both sides by 2. The second solution is (0, 4). Continued. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 5

Graphing Linear Equations Example continued: Graph the linear equation 2 x – y = – 4. For the third solution, let x = – 3. 2(– 3) – y = – 4 – 6–y=– 4+6=2 y=– 2 Replace x with – 3. Simplify the left side. Add 6 to both sides. Multiply both sides by – 1. The third solution is (– 3, – 2). Continued. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 6

Graphing Linear Equations Example continued: y (1, 6) (0, 4) Now plot all three of the solutions (1, 6), (0, 4) and (– 3, – 2). x Draw the line that contains the three points. (– 3, – 2) Martin-Gay, Beginning and Intermediate Algebra, 4 ed 7

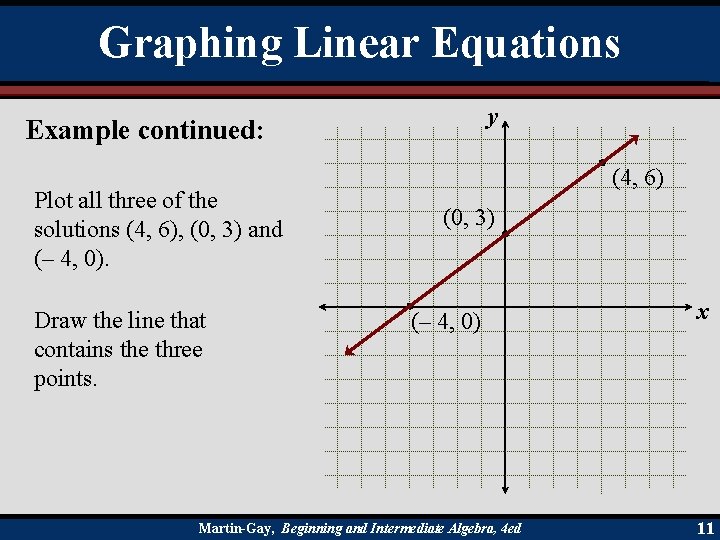
Graphing Linear Equations Example: Graph the linear equation y = x + 3. Let x = 4. y= (4) + 3 y=3+3=6 Replace x with 4. Simplify the right side. One solution is (4, 6). Continued. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 8

Graphing Linear Equations Example continued: Graph the linear equation y = x + 3. For the second solution, let x = 0. y= (0) + 3 y=0+3=3 Replace x with 0. Simplify the right side. So a second solution is (0, 3). Continued. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 9

Graphing Linear Equations Example continued: Graph the linear equation y = x + 3. For the third solution, let x = – 4. y= (– 4) + 3 y=– 3+3=0 Replace x with – 4. Simplify the right side. The third solution is (– 4, 0). Continued. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 10

Graphing Linear Equations y Example continued: Plot all three of the solutions (4, 6), (0, 3) and (– 4, 0). Draw the line that contains the three points. (4, 6) (0, 3) (– 4, 0) Martin-Gay, Beginning and Intermediate Algebra, 4 ed x 11