Electric Potential Chapter 25 The Electric Potential Equipotential

Electric Potential Chapter 25 The Electric Potential Equipotential Surfaces Potential Due to a Distribution of Charges Calculating the Electric Field From the Potential

ELECTRICAL POTENTIAL DIFFERENCE Electrical Potential = Potential Energy per Unit Charge VAB = UAB / q B B VAB = UAB / q = - (1/q) q E. d. L = - E. d. L A B VAB = - E. d. L A A Remember: d. L points from A to B VAB = Electrical potential difference between the points A and B

ELECTRICAL POTENTIAL IN A CONSTANT FIELD E E L A • d. L • B VAB = UAB / q The electrical potential difference between A and B equals the work per unit charge necessary to move a charge +q from A to B VAB = VB – VA = -WAB /q = - E. dl But E = constant, and E. dl = -1 E dl, then: VAB = - E. dl = E dl = E L VAB = E L UAB = q E L

Example: Electric potential of a uniform electric field dr a d a A positive charge would be pushed from regions of high potential to regions of low potential. E b dr d b Remember: since the electric force is conservative, the potential difference does not depend on the integration path, but on the initial and final points. E

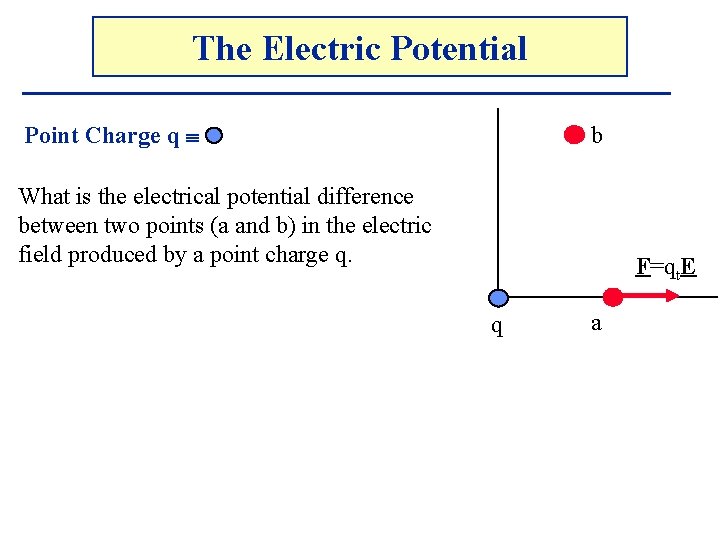
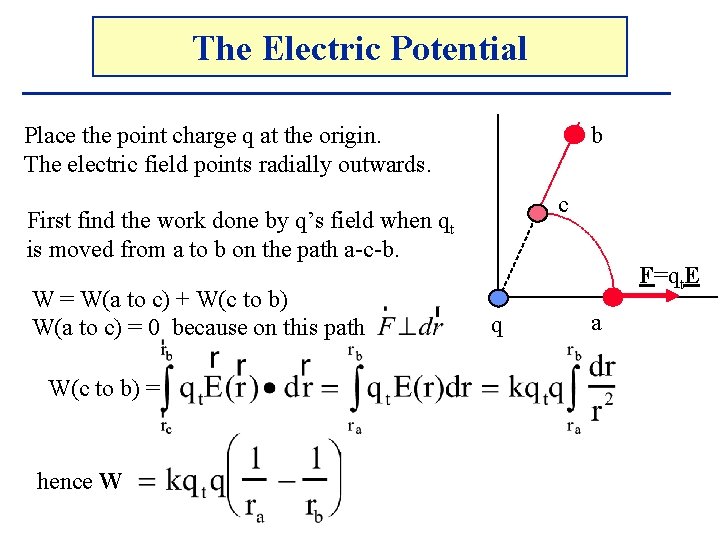
The Electric Potential Point Charge q b What is the electrical potential difference between two points (a and b) in the electric field produced by a point charge q. F=qt. E q a

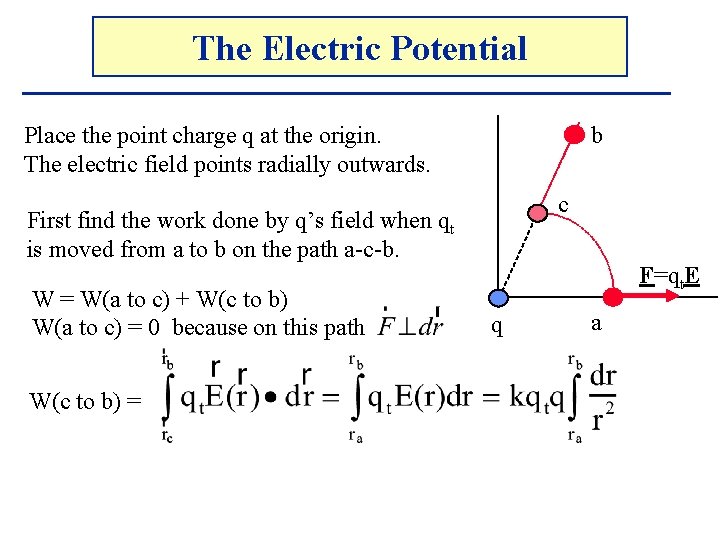
The Electric Potential b Place the point charge q at the origin. The electric field points radially outwards. c First find the work done by q’s field when qt is moved from a to b on the path a-c-b. W = W(a to c) + W(c to b) W(a to c) = 0 because on this path W(c to b) = F=qt. E q a

The Electric Potential b Place the point charge q at the origin. The electric field points radially outwards. c First find the work done by q’s field when qt is moved from a to b on the path a-c-b. W = W(a to c) + W(c to b) W(a to c) = 0 because on this path W(c to b) = hence W F=qt. E q a

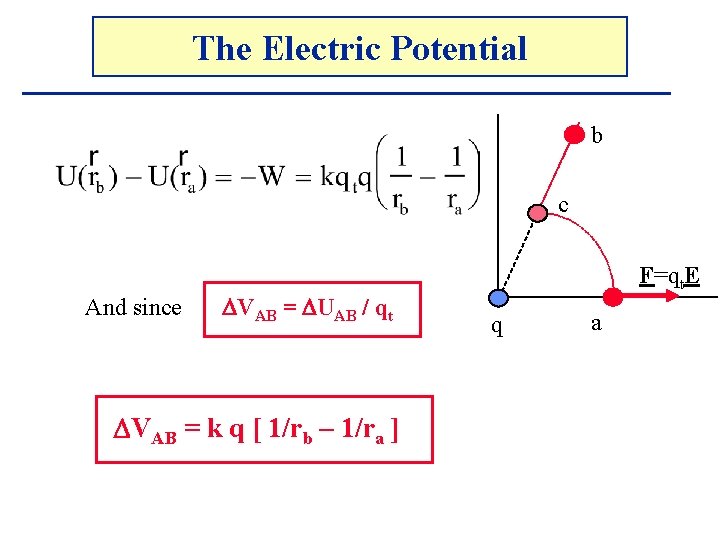
The Electric Potential b c And since VAB = UAB / qt VAB = k q [ 1/rb – 1/ra ] F=qt. E q a

The Electric Potential b VAB = k q [ 1/rb – 1/ra ] c From this it’s natural to choose the zero of electric potential to be when ra Letting a be the point at infinity, and dropping the subscript b, we get the electric potential: V=kq/r F=qt. E q When the source charge is q, and the electric potential is evaluated at the point r. Remember: this is the electric potential with respect to infinity a

Potential Due to a Group of Charges • For isolated point charges just add the potentials created by each charge (superposition) • For a continuous distribution of charge …

Potential Produced by a Continuous Distribution of Charge In the case of a continuous distribution of charge we first divide the distribution up into small pieces, and then we sum the contribution, to the electric potential, from each piece: dqi

Potential Produced by a Continuous Distribution of Charge In the case of a continuous distribution of charge we first divide the distribution up into small pieces, and then we sum the contribution, to the electric potential, from each piece: In the limit of very small pieces, the sum is an integral A r d. V = k dq / r A dq Remember: VA = d. VA = k dq / r vol k=1/(4 0)

Example: a disk of charge Suppose the disk has radius R and a charge per unit area s. Find the potential at a point P up the z axis (centered on the disk). Divide the object into small elements of charge and find the potential d. V at P due to each bit. For a disk, a bit (differential of area) is a small ring of width dw and radius w. P dq = s 2 wdw z r dw w R

Equipotential Surfaces (lines) A E B Since the field E is constant VAB = E L X L E Then, at a distance X from plate A VAX = E X All the points along the dashed line, at X, are at the same potential. The dashed line is an equipotential line L

Equipotential Surfaces (lines) X E It takes no work to move a charge at right angles to an electric field E d. L E • d. L = 0 V = 0 L If a surface (line) is perpendicular to the electric field, all the points in the surface (line) are at the same potential. Such surface (line) is called EQUIPOTENTIAL ELECTRIC FIELD

Equipotential Surfaces We can make graphical representations of the electric potential in the same way as we have created for the electric field: Lines of constant E

Equipotential Surfaces We can make graphical representations of the electric potential in the same way as we have created for the electric field: Lines of constant V (perpendicular to E) Lines of constant E

Equipotential Surfaces We can make graphical representations of the electric potential in the same way as we have created for the electric field: Lines of constant V (perpendicular to E) Lines of constant E Equipotential plots are like contour maps of hills and valleys.

Equipotential Surfaces How do the equipotential surfaces look for: (a) A point charge? E + (b) An electric dipole? + - Equipotential plots are like contour maps of hills and valleys.

Force and Potential Energy Choosing an arbitrary reference point r 0 (such as ) at which U(r 0) = 0, the potential energy is: This can be inverted: The potential energy U is calculated from the force F, and conversely the force F can be calculated from the potential energy U

Field and Electric Potential Dividing the preceding expressions by the (test) charge q we obtain: V (x, y, z) = - E • dr E (x, y, z) = - V V = (d. V/dx) i + (d. V/dy) j + (d. V/dz) k gradient

Example: a disk of charge • • • Suppose the disk has radius R and a charge per unit area s. Find the potential and electric field at a point up the z axis. Divide the object into small elements of charge and find the potential d. V at P due to each bit. So here let a bit be a small P ring of charge width dw and radius w. dq = s 2 wdw z r dw w R

Example: a disk of charge By symmetry one sees that Ex=Ey=0 at P. Find Ez from P z dw This is easier than integrating over the components of vectors. Here we integrate over a scalar and then take partial derivatives. w r R

Example: point charge Put a point charge q at the origin. Find V(r): here this is easy: q r

Example: point charge Put a point charge q at the origin. Find V(r): here this is easy: Then find E(r) from the derivatives: q r

Example: point charge Put a point charge q at the origin. Find V(r): here this is easy: Then find E(r) from the derivatives: Derivative: q r

Example: point charge Put a point charge q at the origin. Find V(r): here this is easy: Then find E(r) from the derivatives: Derivative: So: q r