ELECTRIC POTENTIAL Summer 2008 Chapter 24 Electric Potential

ELECTRIC POTENTIAL Summer , 2008

Chapter 24 Electric Potential In this chapter we will define the electric potential ( symbol V ) associated with the electric force and accomplish the following tasks: Calculate e V if we know the corresponding electric field the electric field if we know the corresponding potential V Determine the potential V generated by a point charge Determine the potential V generated by a continuous charge distribution Determine the electric potential energy U of a system of charges Define the notion of an equipotential surface Explore the geometric relationship between equipotential surfaces and electric field lines Explore the potential of a charged isolated conductor (24 - 1)

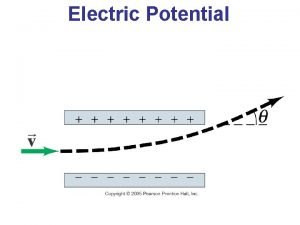
Picture a Region of space Where there is an Electric Field • Imagine there is a particle of charge q at some location. • Imagine that the particle must be moved to another spot within the field. • Work must be done in order to accomplish this.

So, when we move a charge in an Electric Field. . n n Move the charge at constant velocity so it is in mechanical equilibrium all the time. Ignore the acceleration at the beginning because you have to do the same amount of negative work to stop it when you get there.

n When an object is moved from one point to another in an Electric Field, q q q It takes energy (work) to move it. This work can be done by an external force (you). You can also think of this as the FIELD negative of doing the this amount of work on the particle.

The net work done by a conservative (field) force on a particle moving around a closed path is ZERO!

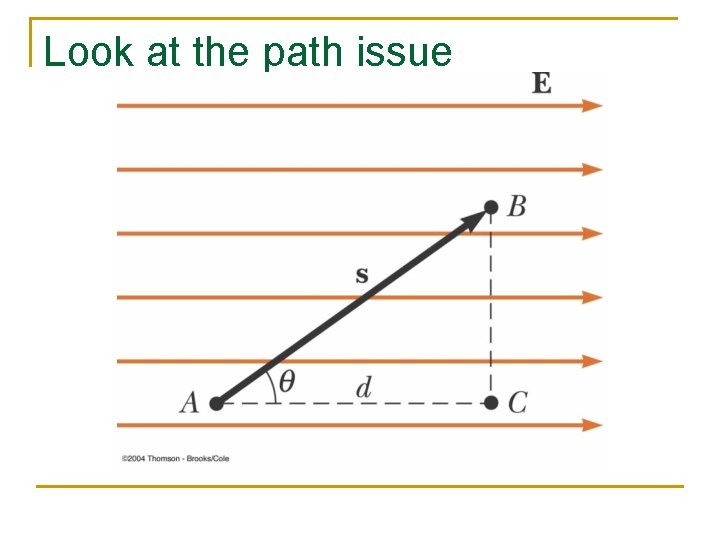
IMPORTANT n The work necessary to move a charge from an initial point to a final point is INDEPENDENT OF THE PATH CHOSEN!

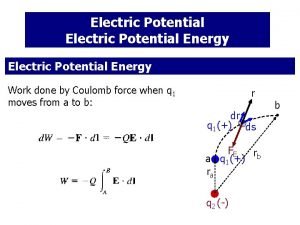
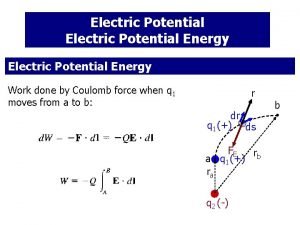
Electric Potential Energy n n n When an electrostatic force acts between two or more charged particles, we can assign an ELECTRIC POTENTIAL ENERGY U to the system. The change in potential energy of a charge is the amount of work that is done by an external force in moving the charge from its initial position to its new position. It is the negative of the work done by the FIELD in moving the particle from the initial to the final position.

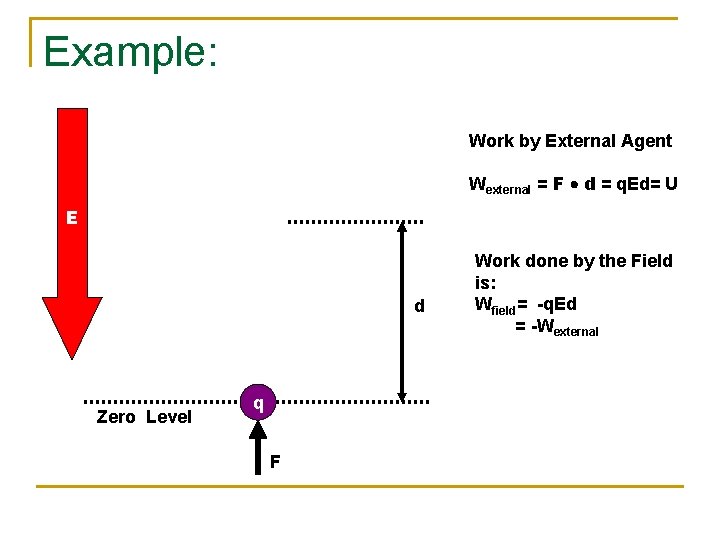
Definition – Potential Energy n n PE or U is the work done by an external agent in moving a charge from a REFERENCE POSITION to a different position. A Reference ZERO is placed at the most convenient position q Like the ground level in many gravitational potential energy problems.

Example: Work by External Agent Wexternal = F d = q. Ed= U E d Zero Level q F Work done by the Field is: Wfield= -q. Ed = -Wexternal

AN IMPORTANT DEFINITION n Just as the ELECTRIC FIELD was defined as the FORCE per UNIT CHARGE: VECTOR We define ELECTRICAL POTENTIAL as the POTENTIAL ENERGY PER UNIT CHARGE: SCALAR

UNITS OF POTENTIAL

Furthermore… If we move a particle through a potential difference of DV, the work from an external “person” necessary to do this is q. DV

Consider Two Plates OOPS …

Look at the path issue

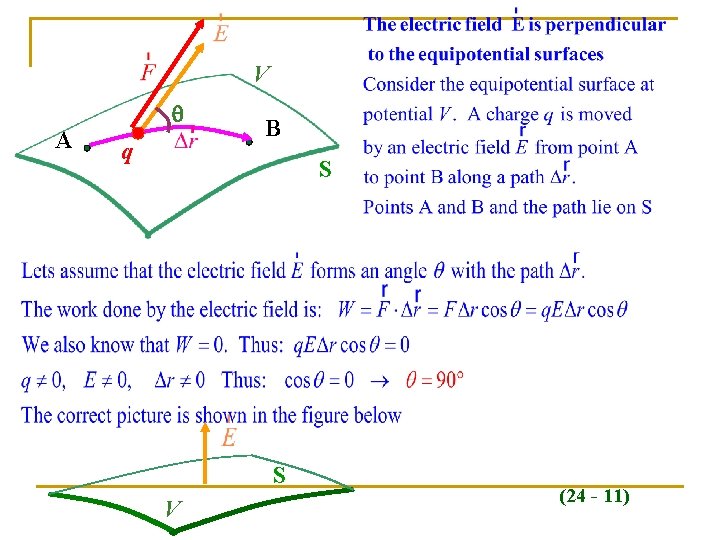
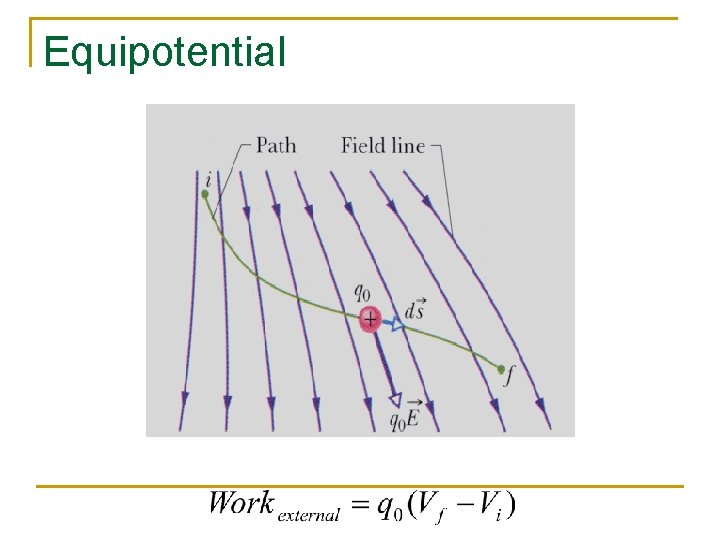
An Equipotential Surface is defined as a surface on which the potential is constant. It takes NO work to move a charged particle between two points at the same potential. The locus of all possible points that require NO WORK to move the charge to is actually a surface.

(24 - 10)

V A q B S S V (24 - 11)

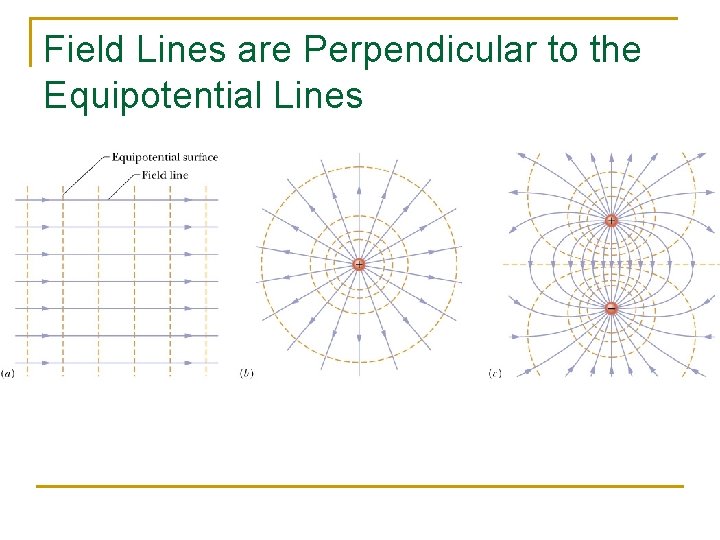
Field Lines are Perpendicular to the Equipotential Lines

Equipotential

Keep in Mind n n Force and Displacement are VECTORS! Potential is a SCALAR.

UNITS n n 1 VOLT = 1 Joule/Coulomb For the electric field, the units of N/C can be converted to: 1 (N/C) = 1 (N/C) x 1(V/(J/C)) x 1 J/(1 NM) Or 1 N/C = 1 V/m n So an acceptable unit for the electric field is now Volts/meter. N/C is still correct as well.

In Atomic Physics n n n It is sometimes useful to define an energy in e. V or electron volts. One e. V is the additional energy that an proton charge would get if it were accelerated through a potential difference of one volt. 1 e. V = e x 1 V = (1. 6 x 10 -19 C) x 1(J/C) = 1. 6 x 10 -19 Joules.

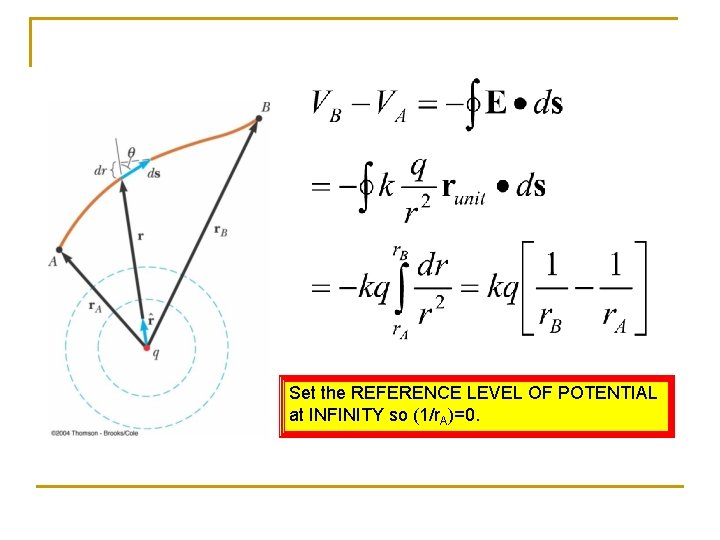
Coulomb Stuff: A NEW REFERENCE: INFINITY Consider a unit charge (+) being brought from infinity to a distance r from a Charge q: q x r To move a unit test charge from infinity to the point at a distance r from the charge q, the external force must do an amount of work that we now can calculate.

Set the REFERENCE LEVEL OF POTENTIAL at INFINITY so (1/r. A)=0.

For point charges

q 1 q 2 q 3 r 1 r 2 P r 3 (24 - 5)

For a DISTRIBUTION of charge:

O dq A (24 - 8)

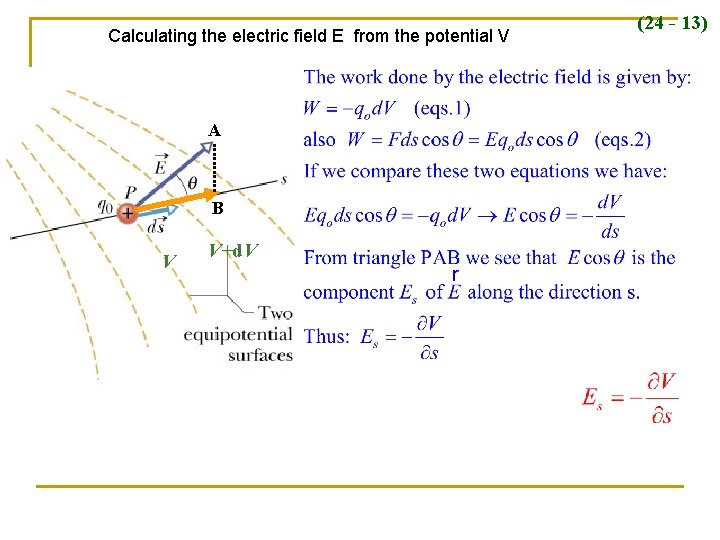
Calculating the electric field E from the potential V A B V V+d. V (24 - 13)

(24 - 14) A B V V+d. V

(24 - 15) q 2 y r 12 r 23 q 1 r 13 O q 3 x

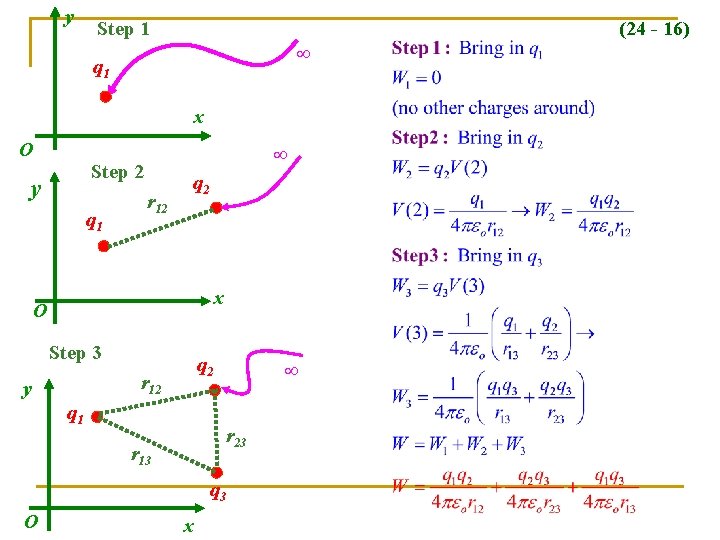
y Step 1 (24 - 16) q 1 x O Step 2 y q 1 r 12 q 2 x O Step 3 q 2 r 12 y q 1 r 23 r 13 q 3 O x

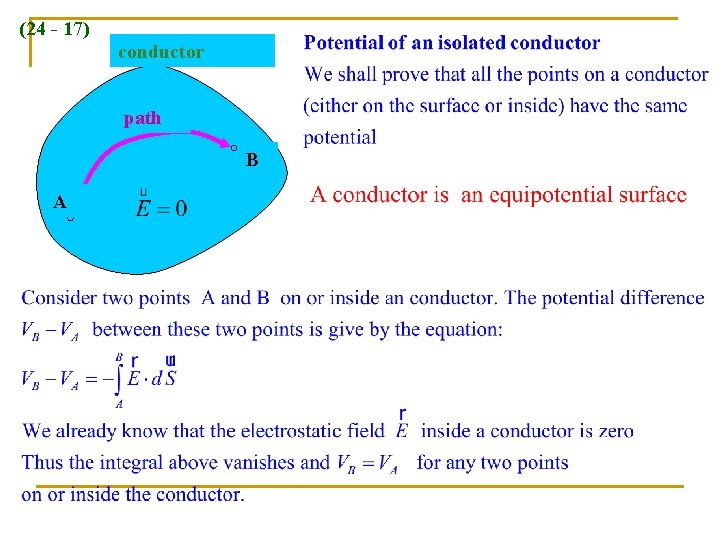
(24 - 17) conductor path B A

(24 - 18)

(24 - 19)

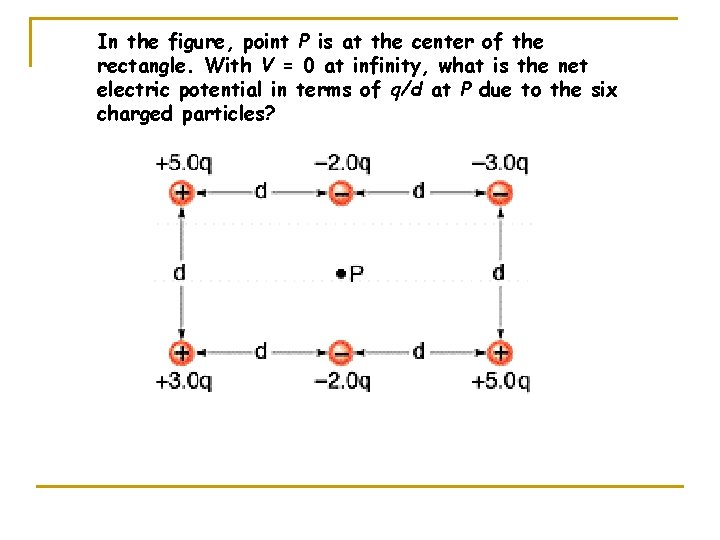
In the figure, point P is at the center of the rectangle. With V = 0 at infinity, what is the net electric potential in terms of q/d at P due to the six charged particles?

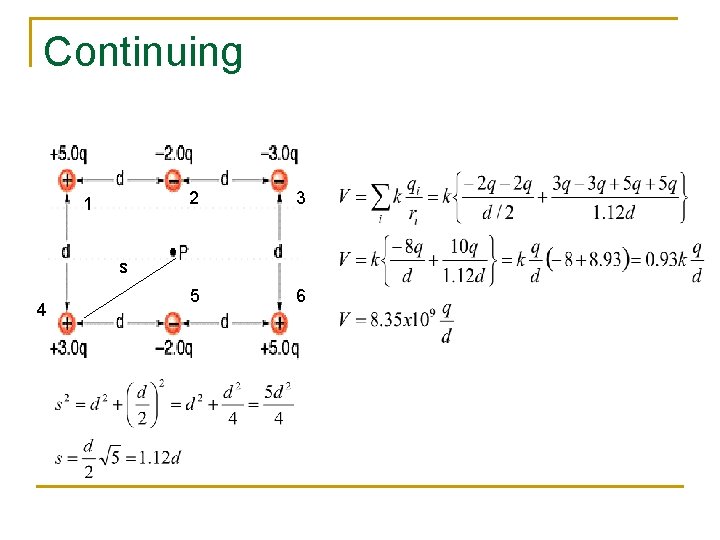
Continuing 1 2 3 5 6 s 4