Chapter 25 Electric Potential ELECTRIC POTENTIAL January 28






































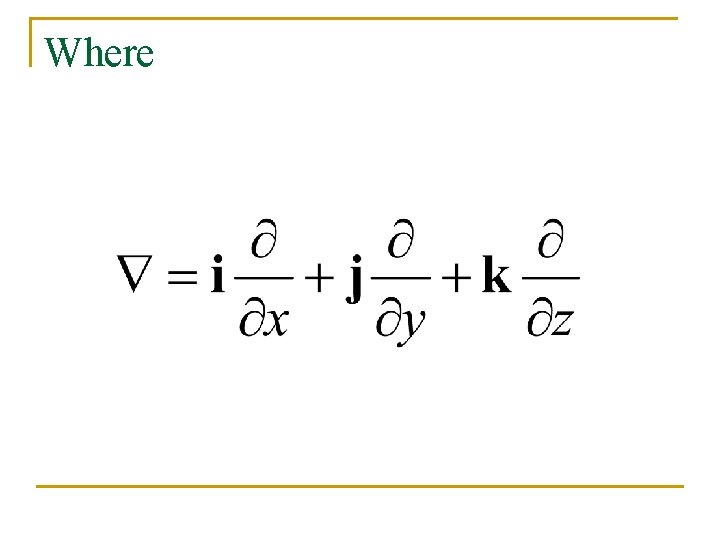






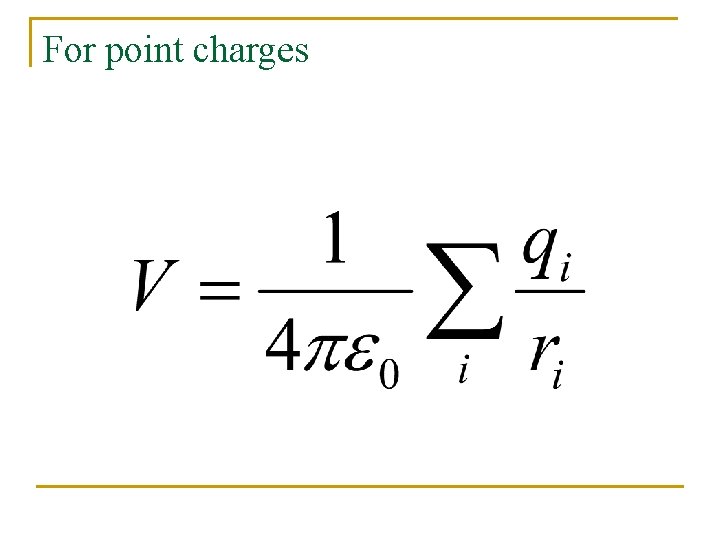






- Slides: 75

Chapter 25 – Electric Potential

ELECTRIC POTENTIAL January 28, 2008

Schedule of Happenings n Today – We had a review session this morning at 7: 30 AM. – We start the topic of Electric Potential – Chapter 25 n Friday – – Examination #1 on Friday § 4 problems § Bring calculators § Brief formula sheet will be provided

ABOUT Web. Assign n Check Daily n Note due time n No more extensions because you didn’t know when an assignment was due.

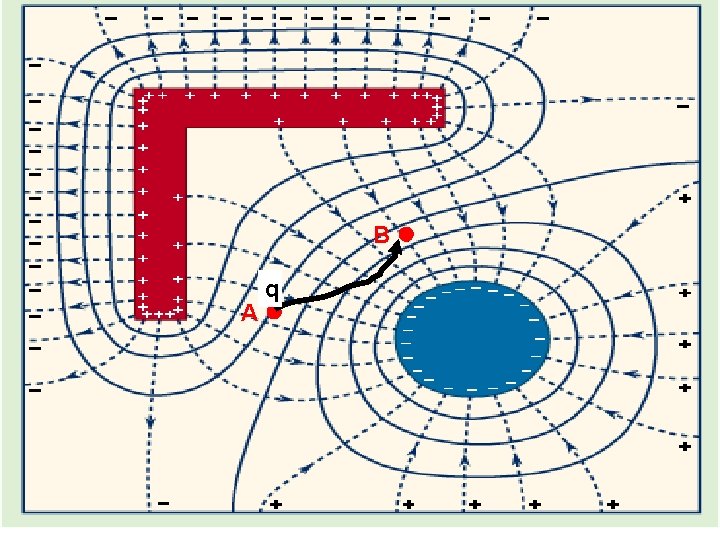
B q A

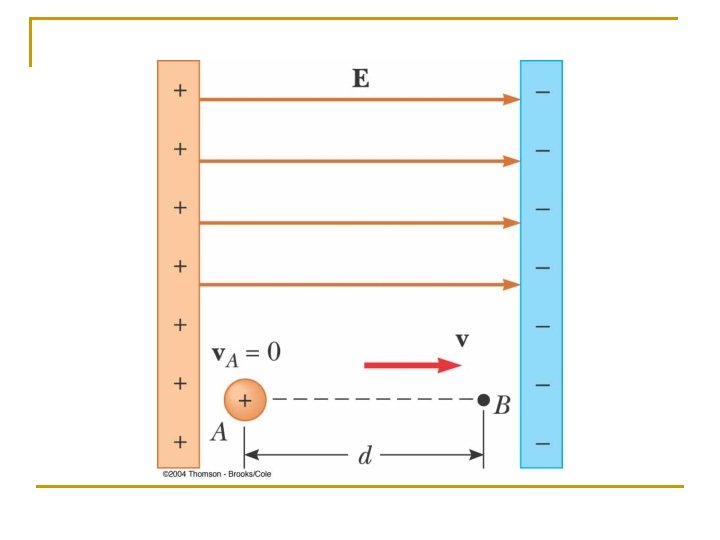
We have a region in space where there is an Electric Field • There is a particle of charge q at some location. • The particle must be moved to another spot within the field. • Work must be done in order to accomplish this.

If the field is E, how much work must be done to move a charge q from one point to another? A. q. Ed where d is the distance moved B. q. E/d C. D. Q(DE)d

Electric Potential n We will be dealing with q q n Work Energy & Conservation Work must be done to move a charge in an electric field. q Let’s do a weird demo ….

I need some help.

What we will do …. E + charge Mrs. Fields n n Mr. External For the moment, assume the charge has MASS. (It may not. ) Assume the charge is initially stationary. The charge is to be moved to the left. The charge is to be moved at CONSTANT velocity.

During this process, who is pushing? A. Mr. External B. Mrs. Fields C. Dr. Bindell

When we start the process, the charge that is stationary must be brought up to speed. A. This is work and must be accounted for. B. This is work but we don’t have to worry about it. C. Only Dr. Bindell worries about stupid stuff like this!

Start and Sop n n n ENERGY is required to bring the charge up to speed (if it has mass). ENERGY is required to bring the particle back to rest (if it has mass). The sum of these two is ZERO.

During this process, who is actually doing work? A. B. C. D. Mr. External Mrs. Fields Both of them Neither of them.

Clearly n n n Both are doing work. BOTH are applying a force through a distance. BOTH get tired!

About the work that they do. . A. Mrs. Fields does more work than Mr. External. B. Mr. External does more work than Mrs. Fields. C. Both do the same amount of work. D. Each does the negative amount of work than the other does.

Each does the negative amount of work than the other does.

So, when we move a charge in an Electric Field. . n n Move the charge at constant velocity so it is in mechanical equilibrium all the time. Ignore the acceleration at the beginning because you have to do the same amount of negative work to stop it when you get there.

Summary-n When an object is moved from one point to another in an Electric Field, q q q It takes energy (work) to move it. This work can be done by an external force (you). You can also think of this as the FIELD negative of doing the this amount of work on the particle.

And also remember: The net work done by a conservative (field) force on a particle moving around a closed path is ZERO!

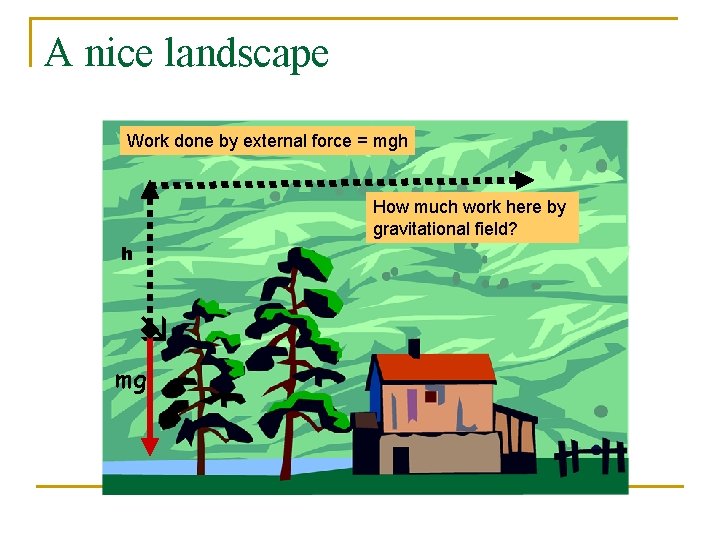
A nice landscape Work done by external force = mgh How much work here by gravitational field? h mg

The gravitational case:

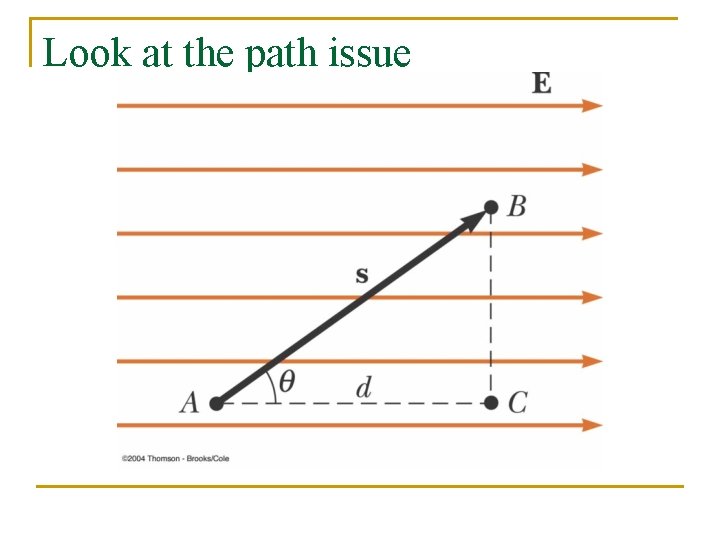
Someone else’s path

IMPORTANT n The work necessary for an external agent to move a charge from an initial point to a final point is INDEPENDENT OF THE PATH CHOSEN!

The Electric Field n Is a conservative field. q n n No frictional losses, etc. Is created by charges. When one (external agent) moves a test charge from one point in a field to another, the external agent must do work. This work is equal to the increase in potential energy of the charge. It is also the NEGATIVE of the work done BY THE FIELD in moving the charge from the same points.

A few things to remember… n n A conservative force is NOT a Republican. An External Agent is NOT 007.

Electric Potential Energy n n n When an electrostatic force acts between two or more charged particles, we can assign an ELECTRIC POTENTIAL ENERGY U to the system. The change in potential energy of a charge is the amount of work that is done by an external force in moving the charge from its initial position to its new position. It is the negative of the work done by the FIELD in moving the particle from the initial to the final position.

Definition – Potential Energy n n PE or U is the work done by an external agent in moving a charge from a REFERENCE POSITION to a different position. A Reference ZERO is placed at the most convenient position q Like the ground level in many gravitational potential energy problems.

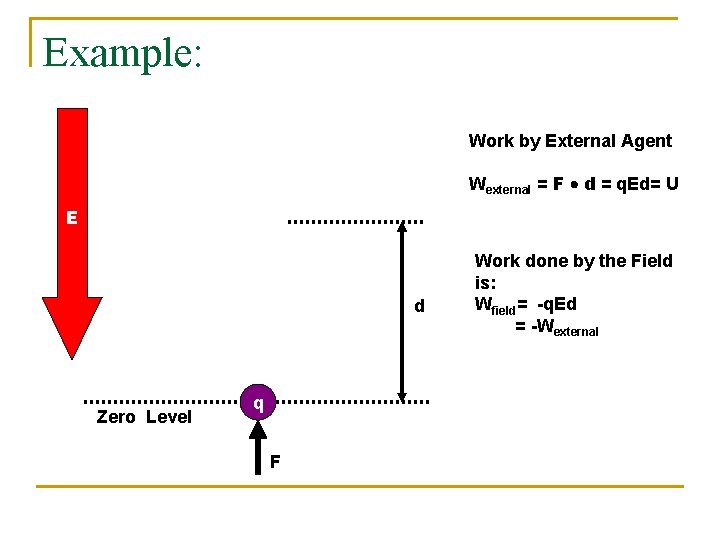
Example: Work by External Agent Wexternal = F d = q. Ed= U E d Zero Level q F Work done by the Field is: Wfield= -q. Ed = -Wexternal

A uniform electric field of magnitude 290 V/m is directed in the positive x direction. A +13. 0 µC charge moves from the origin to the point (x, y) = (20. 0 cm, 50. 0 cm). (a) What is the change in the potential energy of the charge field system? [-0. 000754] J

AN IMPORTANT DEFINITION n Just as the ELECTRIC FIELD was defined as the FORCE per UNIT CHARGE: VECTOR We define ELECTRICAL POTENTIAL as the POTENTIAL ENERGY PER UNIT CHARGE: SCALAR

UNITS OF POTENTIAL

Let’s move a charge from one point to another via an external force. n n The external force does work on the particle. The ELECTRIC FIELD also does work on the particle. We move the particle from point i to point f. The change in kinetic energy is equal to the work done by the applied forces. Assume this is zero for now.

Furthermore… If we move a particle through a potential difference of DV, the work from an external “person” necessary to do this is q. DV

Example Electric Field = 2 N/C 1 m. C d= 100 meters

One Step More

Consider Two Plates OOPS …


Look at the path issue

The difference in potential between the accelerating plates in the electron gun of a TV picture tube is about 25 000 V. If the distance between these plates is 1. 50 cm, what is the magnitude of the uniform electric field in this region?

An ion accelerated through a potential difference of 115 V experiences an increase in kinetic energy of 7. 37 × 10– 17 J. Calculate the charge on the ion.

Important n n We defined an absolute level of potential. To do this, we needed to define a REFERENCE or ZERO level for potential. For a uniform field, it didn’t matter where we placed the reference. For POINT CHARGES, we will see shortly that we must place the level at infinity or the math gets very messy!

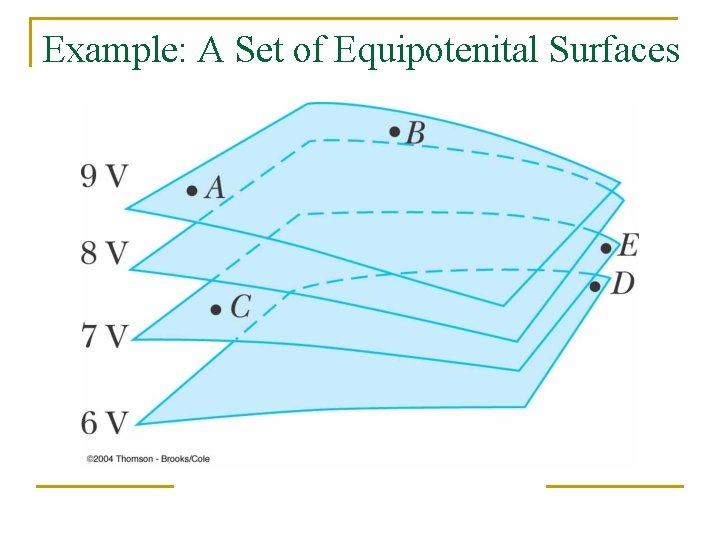
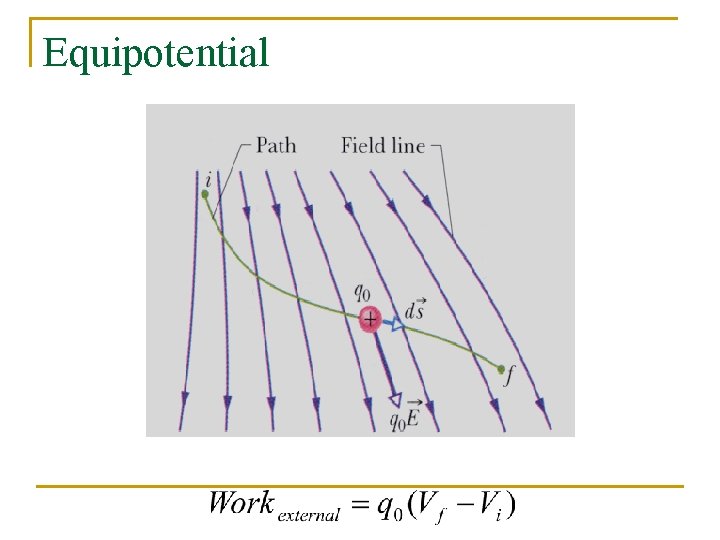
An Equipotential Surface is defined as a surface on which the potential is constant. It takes NO work to move a charged particle between two points at the same potential. The locus of all possible points that require NO WORK to move the charge to is actually a surface.

Example: A Set of Equipotenital Surfaces

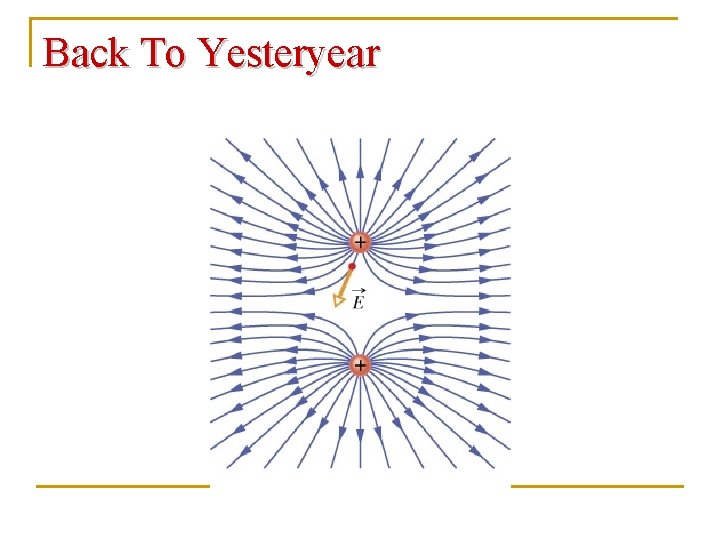
Back To Yesteryear

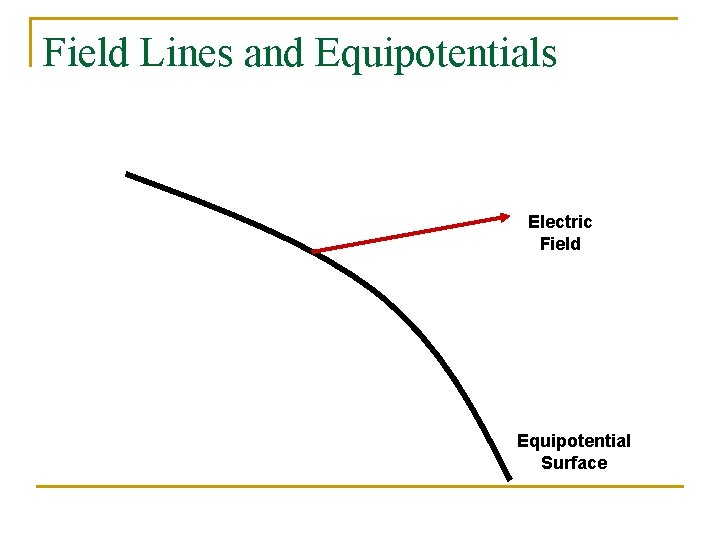
Field Lines and Equipotentials Electric Field Equipotential Surface

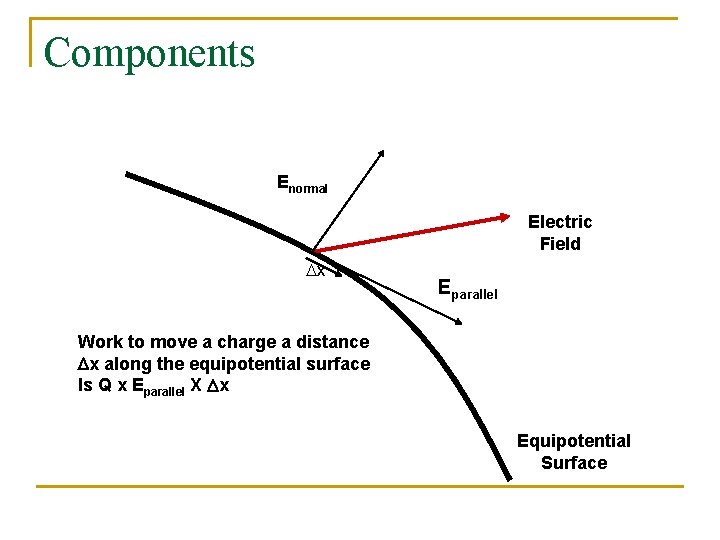
Components Enormal Electric Field Dx Eparallel Work to move a charge a distance Dx along the equipotential surface Is Q x Eparallel X Dx Equipotential Surface

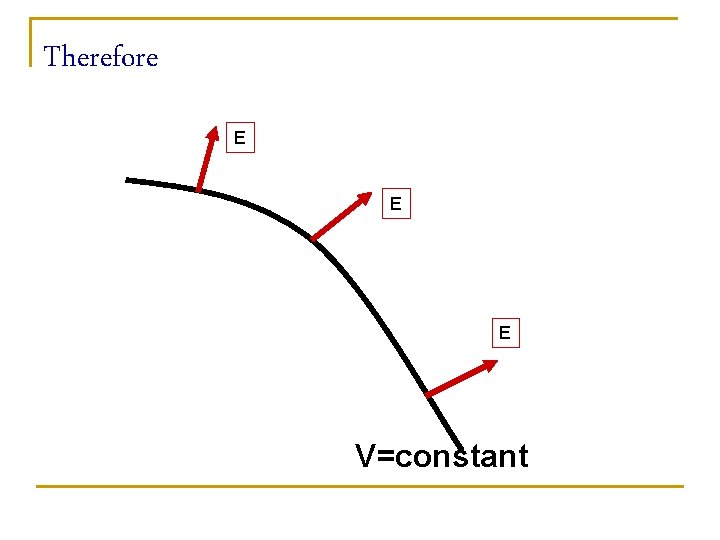
BUT n n This an EQUIPOTENTIAL Surface No work is needed since DV=0 for such a surface. Consequently Eparallel=0 E must be perpendicular to the equipotential surface

Therefore E E E V=constant

Field Lines are Perpendicular to the Equipotential Lines

Equipotential

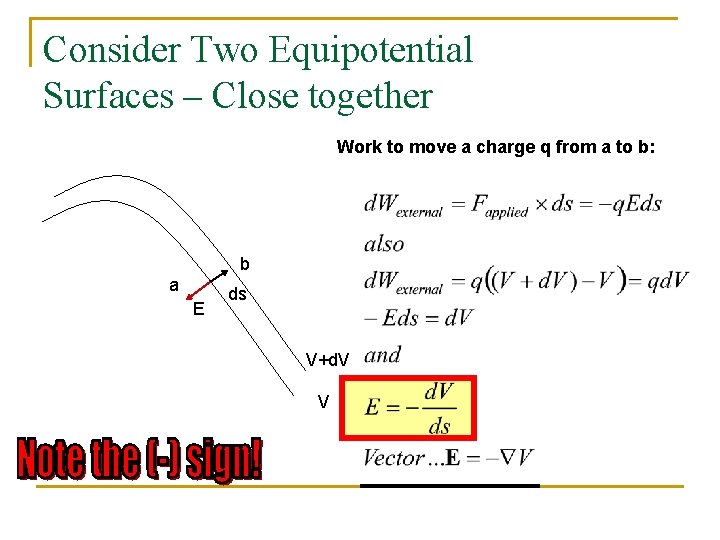
Consider Two Equipotential Surfaces – Close together Work to move a charge q from a to b: b a E ds V+d. V V
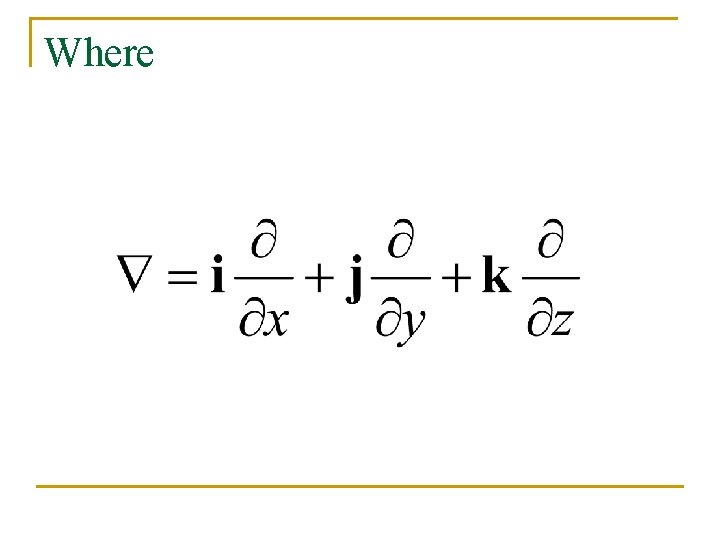
Where

Over a certain region of space, the electric potential is V = 5 x – 3 x 2 y + 2 yz 2. Find the expressions for the x, y, and z components of the electric field over this region. What is the magnitude of the field at the point P that has coordinates (1, 0, – 2) m?

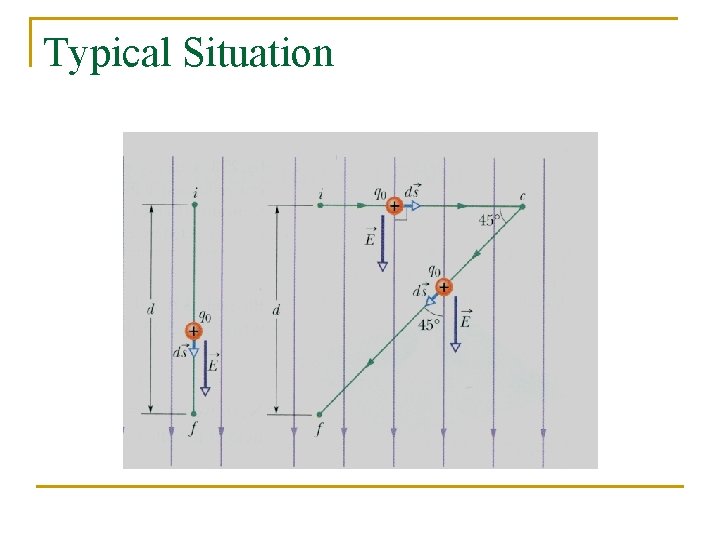
Typical Situation

Keep in Mind n n Force and Displacement are VECTORS! Potential is a SCALAR.

UNITS n n 1 VOLT = 1 Joule/Coulomb For the electric field, the units of N/C can be converted to: 1 (N/C) = 1 (N/C) x 1(V/(J/C)) x 1 J/(1 NM) Or 1 N/C = 1 V/m n So an acceptable unit for the electric field is now Volts/meter. N/C is still correct as well.

In Atomic Physics n n It is sometimes useful to define an energy in e. V or electron volts. One e. V is the additional energy that an proton charge would get if it were accelerated through a potential difference of one volt. 1 e. V = e x 1 V = (1. 6 x 10 -19 C) x 1(J/C) = 1. 6 x 10 -19 Joules. Nothing mysterious.

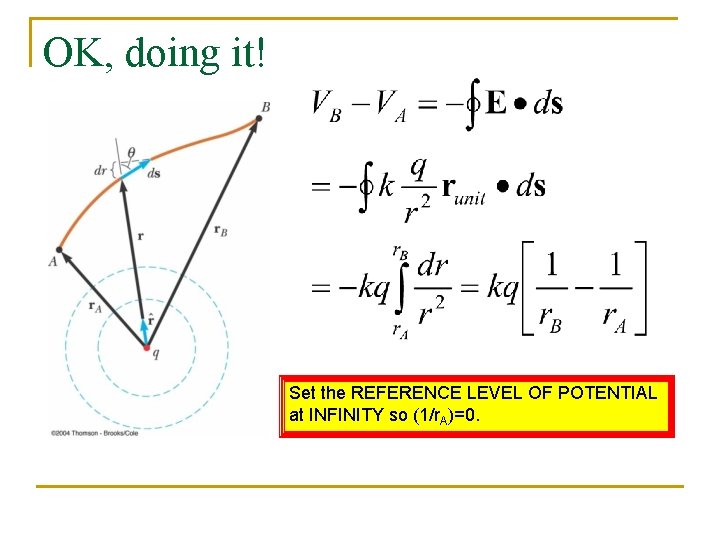
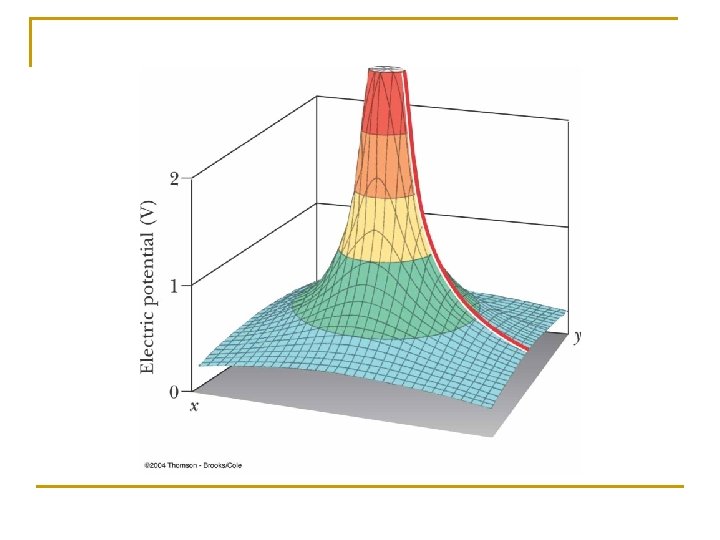
Coulomb Stuff: A NEW REFERENCE: INFINITY Consider a unit charge (+) being brought from infinity to a distance r from a Charge q: q x r To move a unit test charge from infinity to the point at a distance r from the charge q, the external force must do an amount of work that we now can calculate.

Just Do It!

OK, doing it! Set the REFERENCE LEVEL OF POTENTIAL at INFINITY so (1/r. A)=0.
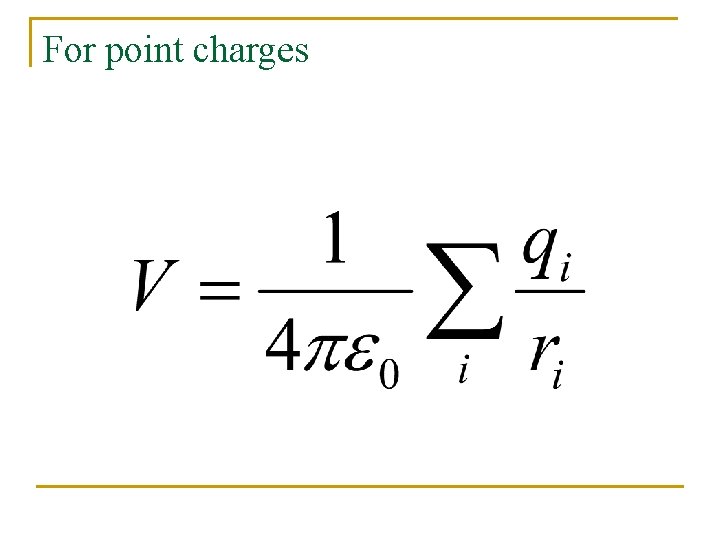
For point charges

For a DISTRIBUTION of charge:



Ponder – What is the potential a distance d from an infinite plane whose charge per unit area is s?

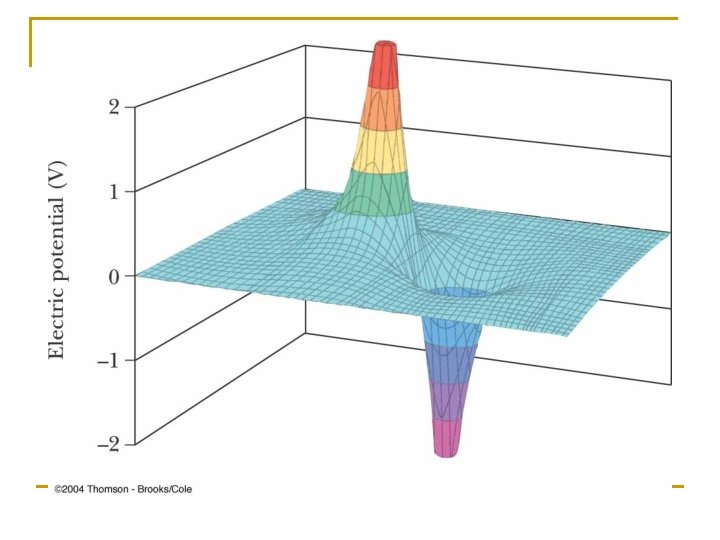
Given two 2. 00 -μC charges, as shown in Figure P 25. 16, and a positive test charge q = 1. 28 × 10– 18 C at the origin, (a) what is the net force exerted by the two 2. 00 -μC charges on the test charge q? (b) What is the electric field at the origin due to the two 2. 00 -μC charges? (c) What is the electrical potential at the origin due to the two 2. 00 -μC charges?

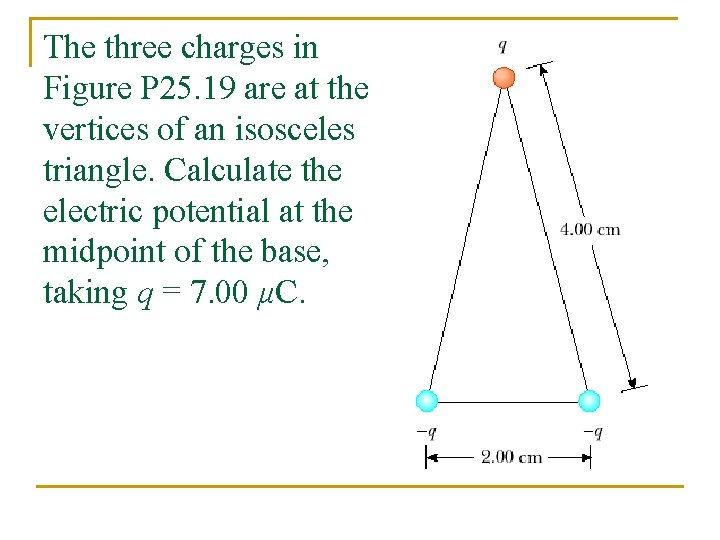
The three charges in Figure P 25. 19 are at the vertices of an isosceles triangle. Calculate the electric potential at the midpoint of the base, taking q = 7. 00 μC.

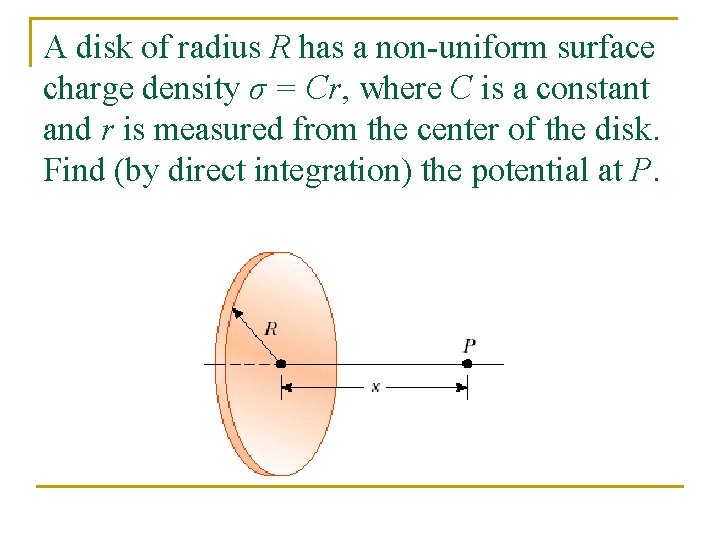
A disk of radius R has a non-uniform surface charge density σ = Cr, where C is a constant and r is measured from the center of the disk. Find (by direct integration) the potential at P.

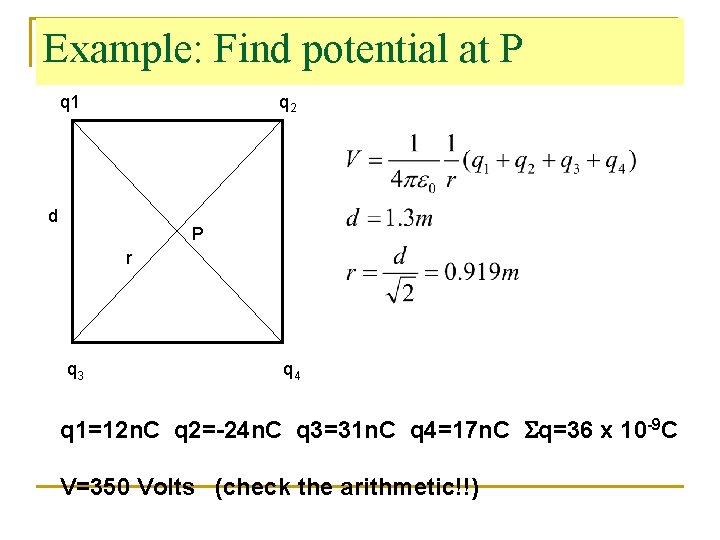
Example: Find potential at P q 1 q 2 d P r q 3 q 4 q 1=12 n. C q 2=-24 n. C q 3=31 n. C q 4=17 n. C Sq=36 x 10 -9 C V=350 Volts (check the arithmetic!!)

An Example finite line of charge x dx r d What about a rod that goes from –L to +L? ? P At P Using table of integrals

Example R z disk s=charge per unit area Which was the result we obtained earlier

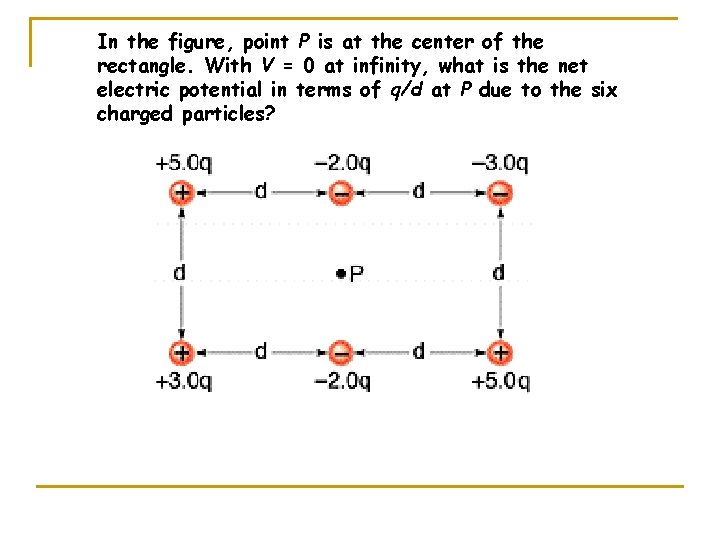
In the figure, point P is at the center of the rectangle. With V = 0 at infinity, what is the net electric potential in terms of q/d at P due to the six charged particles?

Continuing 1 2 3 5 6 s 4 HRW gets 8. 49 … one of us is right!

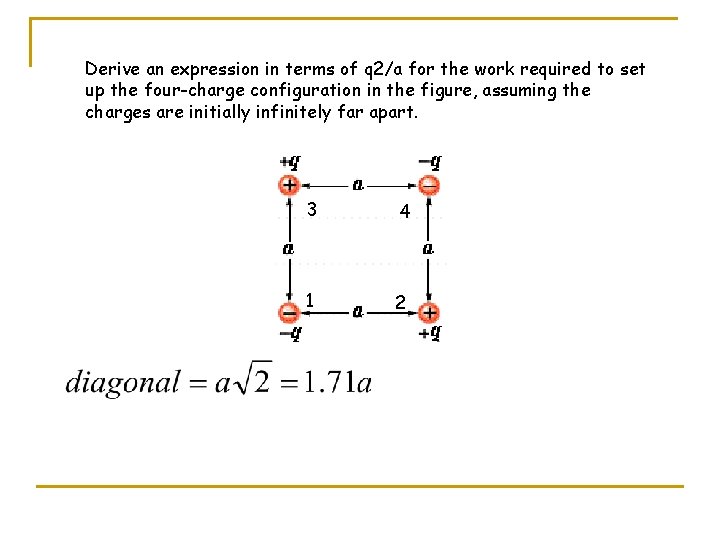
Derive an expression in terms of q 2/a for the work required to set up the four-charge configuration in the figure, assuming the charges are initially infinitely far apart. 3 1 4 2