PHY 102 Lecture 4 4 1 WorkEnergy Review

PHY 102: Lecture 4 • • • 4. 1 Work/Energy Review 4. 2 Electric Potential Energy 4. 3 Concept of Electric Potential 4. 4 Electric Potential 4. 5 Equipotential Surfaces

PHY 102: Lecture 4 Electric Potential Energy Electric Potential 4. 1 Work / Energy Review

Work vs. Energy • Energy is a property of matter – Mass, Inertia and Electric Charge are other properties • Matter that has energy can do work by means of a force • Work transfers or changes energy

Work – Constant Force • Work is a scalar • Work done on an object by a constant force F is: ØW = (F cosq)d • F is magnitude of constant force • d is the magnitude of the displacement along a line q is angle between force and displacement • SI Unit of Work: Newton meter = joule (J)

Kinetic Energy • • • KE = Kinetic Energy KE is the energy of a moving object KE = (1/2)mv 2 m is the mass of the object v is the speed of the object

Work – Energy Theorem • A net external force does work W on an object • The kinetic energy of the object changes from its initial value of KEi to a final value of KEf • The difference between the two values is equal to the work ØW = KEf – KEi = ½ mvf 2 – ½ mvi 2

Work Done by Force of Gravity • An object moves from initial height hi to final height hf • The force of gravity acts on the object ØWgravity = Fd ØF = mg = weight Ød = h i - h f ØWgravity = mg(hi – hf) = mghi - mghf

Gravitational Potential Energy • The gravitational potential energy PE is the energy that an object of mass m has because of its position relative to the surface of the earth • That position is measured by the height h of the object relative to an arbitrary zero level ØPE = mgh

Conservative Force • Version 1 ØA force is conservative when the work it does on a moving object is independent of the path between the object’s initial and final position • Version 2 ØA force is conservative when it does no net work on an object moving around a closed path starting and finishing at the same point

Conservative Forces Nonconservative Forces • Conservative Forces – Gravity – Spring force – Electrostatic force – Magnetic force • Nonconservative Forces – Friction – Air resistance

Principle Conservation of Mechanical Energy • Total mechanical energy (E = KE + PE) of an object remains constant as the object moves • Provided that the net work done by external nonconservative forces is zero, Wnc = 0 J

Kinetic Energy vs. Potential Energy • The sum of the kinetic and potential energies at any point is conserved • Kinetic and Potential Energies may be converted or transformed into one another

PHY 102: Lecture 4 Electric Potential Energy Electric Potential 4. 2 Electric Potential Energy

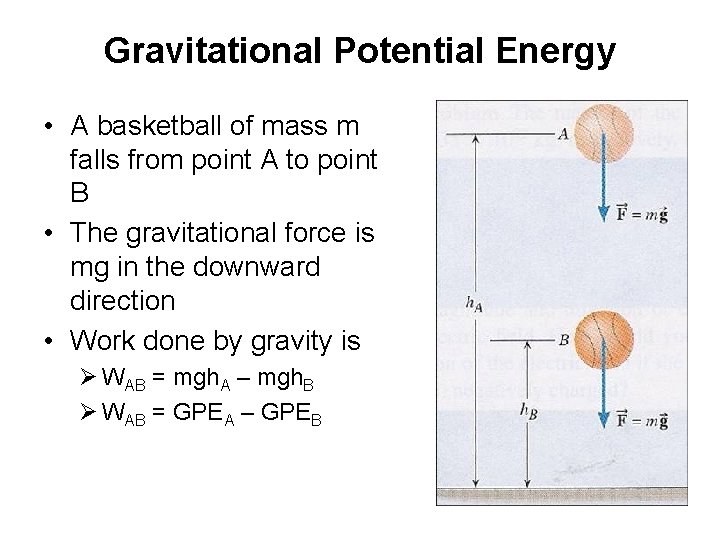
Gravitational Potential Energy • A basketball of mass m falls from point A to point B • The gravitational force is mg in the downward direction • Work done by gravity is Ø WAB = mgh. A – mgh. B Ø WAB = GPEA – GPEB

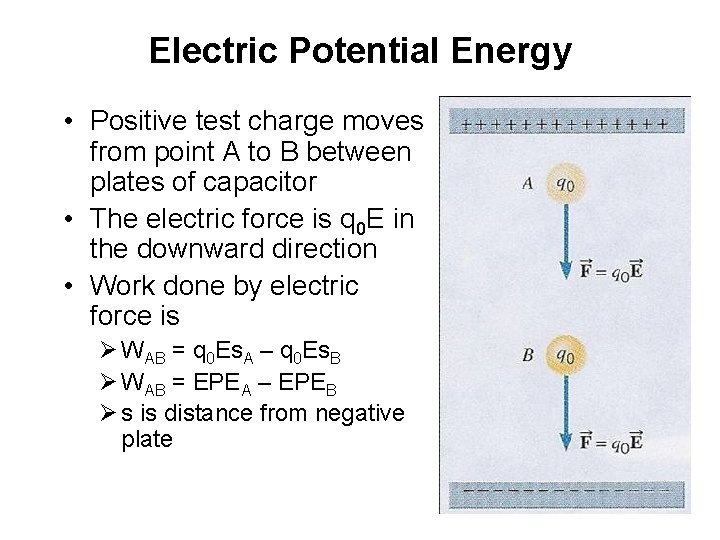
Electric Potential Energy • Positive test charge moves from point A to B between plates of capacitor • The electric force is q 0 E in the downward direction • Work done by electric force is Ø WAB = q 0 Es. A – q 0 Es. B Ø WAB = EPEA – EPEB Ø s is distance from negative plate

Work by Gravity / Electricity • The gravitational and electrical forces are conservative • The work done in going from point A to point B does not depend on the path taken

PHY 102: Lecture 4 Electric Potential Energy Electric Potential 4. 3 Concept of Electric Potential

Concept of Electric Potential-1 • We introduced the concept of the electric field because action at a distance raised concerns and difficulties • The field provides an intermediary through which two charges exert forces on each other • Charge q 1 somehow alters the space around it by creating an electric field E 1 • Charge q 2 then responds to the field experiencing force F = q 2 E 1

Concept of Electric Potential-2 • When we try to understand electric potential energy we face the same kinds of difficulties that action at a distance presented to an understanding of electric force • When we say two charged particles have a potential energy that can be converted to a tangible kinetic energy of motion, where is the energy? • Two positive charges fly apart when you release them gaining kinetic energy • There is no obvious place that the energy had been stored

Concept of Electric Potential-3 • In defining electric field, we chose to separate the charges that are the source of the field from the charge in the field • The force on charge q is related to the electric field of the source charges by Ø force on charge q = [charge q] x [alteration of space by source charge or E field]

Concept of Electric Potential-4 • Try a similar procedure for the potential energy • Electric potential energy is due to the interaction of charge q with other charges • Divide up the potential energy of the system potential energy of (q + sources) = [charge q] x [potential for interaction of the source charges]

Concept of Electric Potential-5 • We define electric potential V (or just the potential) as V = Electric Potential Energyq+sources / q • Charge q is used as a probe to determine the electric potential, but the value of V is independent of q • The electric potential is a property of the source charges

What Good is the Electric Potential? • The electric potential is an abstract idea • Electric potential depends only on source charges and their geometry • The potential is the “ability” of the source charges to have an interaction if a charge q shows up • This ability, or potential, is present throughout space regardless of whether or not charge q is there to experience it • If we know the electric potential V throughout a region of space, we’ll immediately know the potential energy • The source charges exert influence through the electric potential they establish throughout space • Once we know the potential we can ignore the source charges and work just with the potential • The source charges remain hidden offstage

PHY 102: Lecture 4 Electric Potential Energy Electric Potential 4. 4 Electric Potential

Electric Potential Energy • The electric force and the work it does as the charge moves from A to B depends on the charge q 0 • It is useful to express this work on a per-unit-charge basis, by dividing both sides by the charge: üWAB/q 0 = EPEA /q 0 - EPEB/q 0

Electric Potential • The right-hand side of this equation is the difference between two terms • Each of which is an electric potential energy divided by the test charge, EPE/q 0 • The quantity EPE/q 0 is the electric potential energy per unit charge • It is called the electric potential or the potential • It Is referred to with the symbol V • SI Unit: joules/coulomb = volt (V)

Work Related to Electric Potential • Work WAB done by the electric force when a charge q 0 moves from A to B üVB – VA = EPEB/q 0 – EPEA/q 0 = -WAB/q 0 üDV = D(EPE)/q 0 = -WAB/q 0

Problem 1 • Work done by the electric force as the test charge (q 0 = +2. 0 x 10 -6 C) moves from A to B is WAB = +5. 0 x 10 -5 J • (a) Find value of D(EPE) = EPEB – EPEA • (b) Find potential difference DV = VB – VA VA has a higher potential then VB

Potential Size vs Charge Acceleration - 1 • Positive charge accelerates as it moves from A to B because of the electric repulsion from the upper plate and the attraction to the lower plate • Point A has higher electric potential than point B • A positive charge accelerates from a region of higher electric potential toward a region of lower electric potential. • A negative charge accelerates from a region of lower electric potential toward a region of higher electric potential.

Potential Size vs Charge Acceleration - 2 • Positive charge accelerates as it moves from A to B because of the electric repulsion from the upper plate and the attraction to the lower plate • Positive charge increases in speed and kinetic energy • The increase in kinetic energy comes from a decease in electric potential energy • Point A must have higher potential energy

Problem 2 - 1 • A particle has a mass of 1. 8 x 10 -5 kg and a charge of +3. 0 x 10 -5 C • It is released from rest at point A and accelerated until it reaches point B • The only force acting on the particle is an electrostatic force • The electric potential at A is 25 V greater than that at B (VA – VB = 25 V) • What is speed of the particle at point B?

Problem 2 - 2 • This is a conservation of energy problem

Electric Potential Difference of Point Charge - 1 • Positive point charge +q creates an electric potential • There are two locations A and B, at distances r. A and r. B from the charge • An electrostatic force of repulsion acts on a positive test charge +q 0 • Coulomb’s law is F = kq 0 q/r 2 • When the test charge moves from A to B, work is done by this force • F varies between r. A and r. B • Work is not the product of force and distance between the points • Work WAB is found using calculus • The result is ü WAB = kqq 0/r. A – kqq 0/r. B

Electric Potential Difference of Point Charge - 2 • • This result is valid Whether q is “+” or “-” Whether q 0 is “+” or “-” Potential difference VB–VA can now be determined by substituting this expression for WAB into the equation Ø VB – VA = -WAB/q 0 Ø VB – VA = kq/r. B – kq/r. A

Electric Potential of Point Charge - 1 • Let point B be located farther and farther from the charge q • r. B becomes larger and larger • In the limit that r. B is infinitely large, the term kq/r. B becomes zero • It is customary to set VB equal to zero also • In this limit, the equation becomes VA = kq/r. A • It is standard convention to omit the subscripts • Write the potential in the following form • Potential of a point charge V = kq/r

Electric Potential of Point Charge - 2 • The symbol V does not refer to the potential in an absolute sense • V = kq/r stands for the amount by which the potential at a distance r from a point charge differs from the potential at an infinite distance away • In other words, V refers to potential difference with the arbitrary assumption that the potential at infinity is zero

Electric Potential of Point Charge - 3 • When q is positive, the value of V = kq/r is also positive • Indicating that the positive charge has everywhere raised the potential above the zero reference value • When q is negative, the potential V is also negative • Indicting that the negative charge has every where decreased the potential below the zero reference value

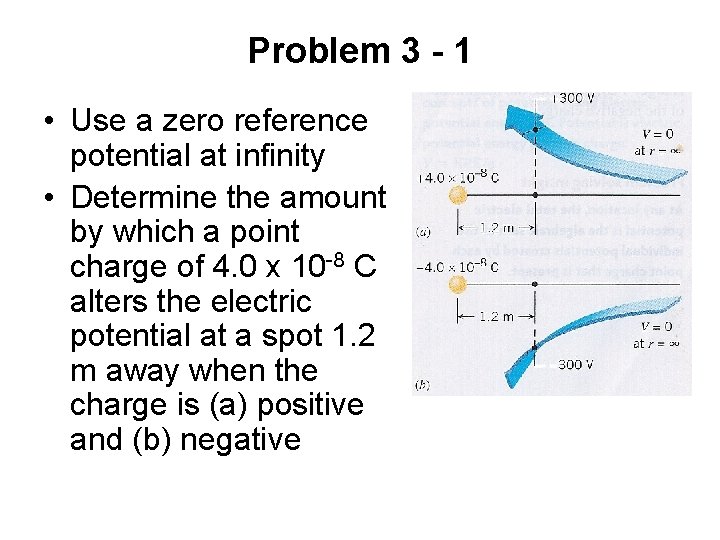
Problem 3 - 1 • Use a zero reference potential at infinity • Determine the amount by which a point charge of 4. 0 x 10 -8 C alters the electric potential at a spot 1. 2 m away when the charge is (a) positive and (b) negative

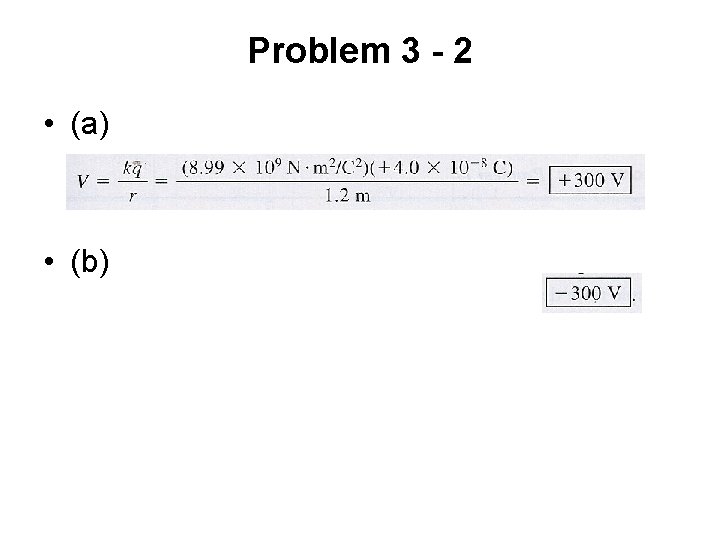
Problem 3 - 2 • (a) • (b)

Electric Potential of More Than 1 Point Charge • Two or more charges are present • The potential due to all charges is obtained by adding together the individual potentials

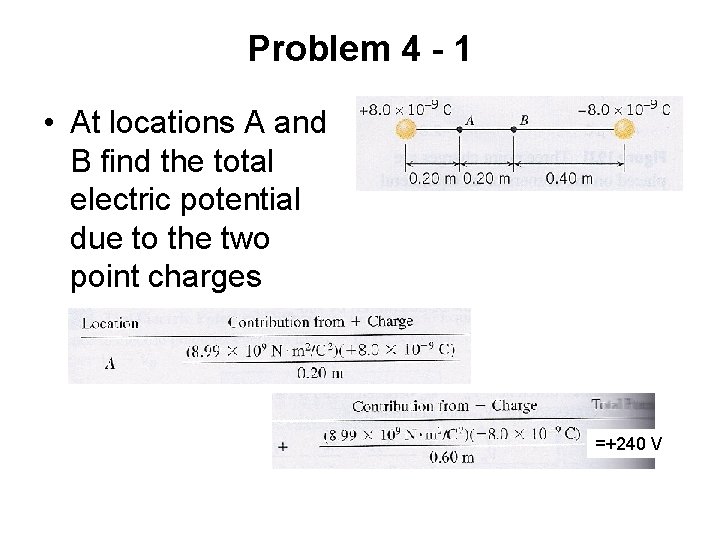
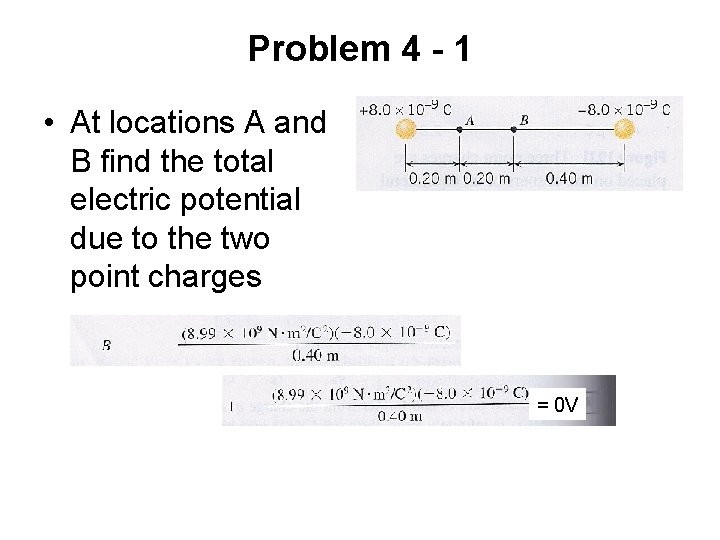
Problem 4 - 1 • At locations A and B find the total electric potential due to the two point charges =+240 V

Problem 4 - 1 • At locations A and B find the total electric potential due to the two point charges ==+0 0 V V

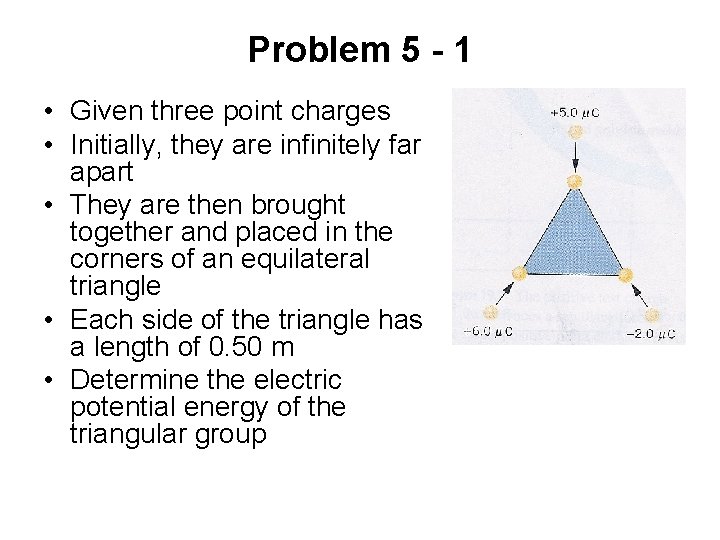
Problem 5 - 1 • Given three point charges • Initially, they are infinitely far apart • They are then brought together and placed in the corners of an equilateral triangle • Each side of the triangle has a length of 0. 50 m • Determine the electric potential energy of the triangular group

Problem 5 - 2 • The order in which the charges are put on the triangle does not matter • We begin with the charge of +5. 0 m. C • When this charge is placed at a corner of the triangle, it has no electric potential energy • The total potential V produced by the other two charges is zero since they are infinitely far away • EPE = q 0 V • V=0 • EPE =0

Problem 5 - 3 • Once the first charge is in place, the potential at the other corners is • When the +6. 0 m. C charge is placed at the second corner

Problem 5 - 4 • The electric potential at the remaining corner is • When the third charge, - 2. 0 m. C, at the remaining empty corner, the electrical potential energy is

Problem 5 - 5 • The total potential energy of the three charges is

PHY 102: Lecture 4 Electric Potential Energy Electric Potential 4. 5 Equipotential Surfaces

Equipotential Surfaces • An equipotential surface is a surface on which the electric potential is the same everywhere • The net electric force does no work as a charge moves on an equipotential surface. • VB – VA = -WAB/q 0 • On the equipotential surface VA = VB Therefore WAB = 0

Equipotential Surfaces for Point Charge • Equipotential surfaces that surround the point charge +q are spherical • As you move from point A to B to C, the electric force does no work because they lie on an equipotential surface • Work is done as you move from point A to D

Relation between Electric Field Lines and Equipotential Surfaces • Electric field created by any charge or group of charges is everywhere perpendicular to the associated equipotential surfaces • Electric field points in the direction of decreasing potential • Surface of any conductor is an equipotential surface • The electric field is zero everywhere inside a conductor • The entire conductor can be regarded as an equipotential volume

Parallel Plate Capacitor Equipotential Surfaces • Electric field E between the metal plates is perpendicular to them • Electric field E is the same everywhere • The equipotential surfaces are planes that are parallel to the capacitor plates • The capacitor plates are also equipotential surfaces

Parallel Plate Capacitor Relation between E and DV • • • Potential difference between plates is given by ΔV = VB – VA = -WAB/q 0 A is point on positive plate and B is point on negative plate The work done by the electric force as a positive test charge q 0 moves from A to B is WAB = FDs F refers to the electric force and Ds to the displacement along a line perpendicular to the plates F = q 0 E Work becomes WAB = FDs = q 0 EDs This leads to E = - DV / Ds The quantity DV / Ds is referred to as the potential gradient This relationship gives only the component of electric field along the displacement Ds

Problem 6 - 1 • The plates of a capacitor are separated by a distance of 0. 032 m • The potential difference between them is DV = VB – VA = -64 V • Between the two labeled equipotential surfaces there is a potential difference of -3. 0 V • Find the spacing between the two labeled surfaces

Problem 6 - 2 • The electric field between the capacitor plates is ü E = - DV/DS ü E = -64 V/0. 032 m ü E = 2. 0 x 103 V/m • Spacing between labeled equipotential surfaces is – DS = -DV/E – DS = -3. 0 V/2. 0 x 103 V/m – DS = 1. 5 x 10 -3 m

Capacitor - 1 • A parallel plate capacitor consists of two parallel metal plates placed near one another but not touching • In general, a capacitor consists of two conductors of any shape placed near one another without touching • It is common practice to fill the region between the conductors or plates with an electrically insulating material called a dielectric

Capacitor - 2 • A capacitor stores electric charge • Each capacitor plate carries a charge of the same magnitude • One positive and the other negative • Because of the charges, the electric potential of the positive plate exceeds that of the negative plate by an amount V • When the magnitude q of the charge on each plate is doubled, the magnitude V of the electric potential difference is also doubled • q is proportional to V

Relationship between q and V • The magnitude q of the charge on each plate of a capacitor is directly proportional to the magnitude V of the potential difference between the plates üq = CV • C is the capacitance • SI Unit of Capacitance: coulomb/volt = farad (F)

Capacitance • One farad is an enormous capacitance • Usually smaller amounts, such as a microfarad, are used in electric circuits

Dielectric - 1 • A dielectric is inserted between the plates of a capacitor • The capacitance increases markedly because of the way in which the dielectric alters the electric field between the plates

Dielectric - 2 • The region between the charged plates is empty • The field lines point from the positive toward the negative plate

Dielectric - 3 • • • The charge on the plates remains constant as the dielectric is inserted In many materials the molecules possess permanent dipole moments, even though the molecules are electrically neutral The dipole moment exists because one end of a molecule has slight excess of negative charge while the other end has a slight excess of positive charge When such molecules are placed between the charged plates of the capacitor, the negative ends are attracted to the positive plate and the positive ends are attracted to the negative plate As a result, the dipolar molecules tend to orient themselves end-to-end Left surface of the dielectric is positively charged and the right surface is negatively charged

Dielectric - 4 • • Because of the surface charges on the dielectric, not all the electric field lines generated by the charges on the plates pass through the dielectric Some of the field lines end on the negative surface charges And begin again on the positive surface charges Thus, the electric field inside the dielectric is less strong than the electric field inside the empty capacitor, assuming the charge on the plates remains constant This reduction in the electric field is described by the dielectric constant , which is the ratio of the field magnitude E 0 without the dielectric to the field magnitude E inside the dielectric: K = E 0 / E Moreover, since the field E 0 without the dielectric is greater than the field E inside the dielectric; the dielectric constant is greater than unity

Capacitance of Parallel Plate Capacitor • • • • • Given a parallel plate capacitor in which the area of each plate is A and the separation between the plates is d The magnitude of the electric field inside the dielectric is given by as E = V/d V is the magnitude of the potential difference between the plates The electric field inside the dielectric is related to the electric field in the absence of the dielectric E = E 0/K = V/d Since the electric field within an empty capacitor is E 0 = q / (e 0 A), it follows that q / (Ke 0 A) = V/d which can be solved for q to give q = (Ke 0 A / d)V A comparison of this express with q = CV reveals that the capacitance C is Parallel place capacitor filled with a dielectric C = (Ke 0 A/d) With C 0 representing the capacitance of the empty capacitor (K = 1) C = KC 0 In other words, the capacitance with the dielectric present is increased by a factor of K over the capacitance without the dielectric The relation C = KC 0 applies to any capacitor, not just to a parallel plate capacitor

Energy Storage in Capacitor • • • Energy = ½ q. V Energy = ½ (CV)V = ½ CV 2 Energy = ½ q(q/C) = q 2/2 C Energy = ½ CV 2 = ½ (Ke 0 A / d)(Ed)2 Energy Density=Energy/Volume = ½Ke 0 E 2