EAL ET 005 A Further Engineering Science Lecture

EAL ET 005 A Further Engineering Science Lecture 10 Engineering Systems

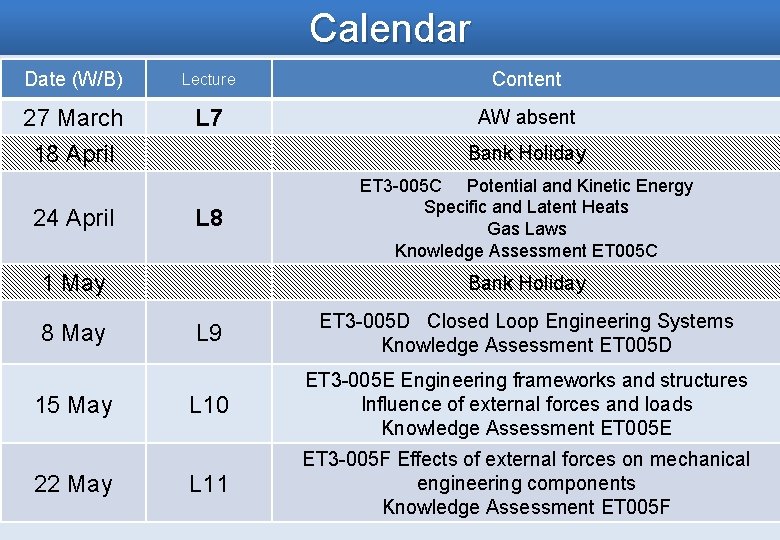
Calendar Date (W/B) Lecture Content 27 March 18 April L 7 AW absent 24 April Bank Holiday L 8 ET 3 -005 C Potential and Kinetic Energy Specific and Latent Heats Gas Laws Knowledge Assessment ET 005 C 1 May Bank Holiday 8 May L 9 ET 3 -005 D Closed Loop Engineering Systems Knowledge Assessment ET 005 D L 10 ET 3 -005 E Engineering frameworks and structures Influence of external forces and loads Knowledge Assessment ET 005 E L 11 ET 3 -005 F Effects of external forces on mechanical engineering components Knowledge Assessment ET 005 F 15 May 22 May

UNIT 003 Learning Outcomes Learning Aim : Understand the effect of forces in static equilibrium for a system NOTE: This UNIT IS ASSESSED through EIGHT Knowledge Assessment Tests and THREE Practical Tests

Objectives Having completed this lecture, you will be able to: - § Apply and recognise static structures involving point forces, torque and distributed forces. § Understand how to calculate stress forces on structures using moments and resolution of forces. Use to given safety factors. § Recognise and use Young’s Modulus to calculate stress and strain values.

09/09/2021 Review of forces acting on objects Static and Dynamic Equilibrium of forces Equilibrium means the object is at rest (static) or its centre of mass moves with a constant velocity (dynamic) Examples Book on table Hanging sign Ceiling fan – off Ladder leaning against wall A bridge A hanging shop sign Ceiling fan – on An aircraft We will only look at the case in where linear and angular velocities are equal to zero, called “static equilibrium” i. e. Net external force must equal zero Net external torque (turning force) must equal zero

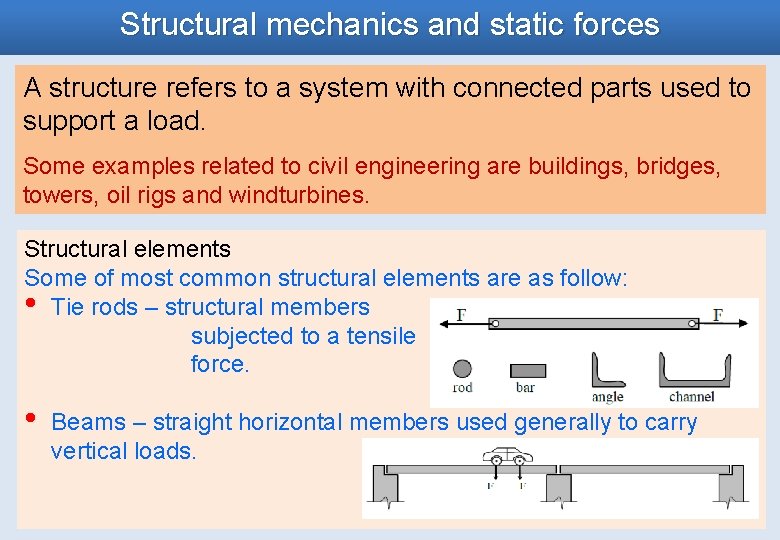
Structural mechanics and static forces A structure refers to a system with connected parts used to support a load. Some examples related to civil engineering are buildings, bridges, towers, oil rigs and windturbines. Structural elements Some of most common structural elements are as follow: • Tie rods – structural members subjected to a tensile force. • Beams – straight horizontal members used generally to carry vertical loads.

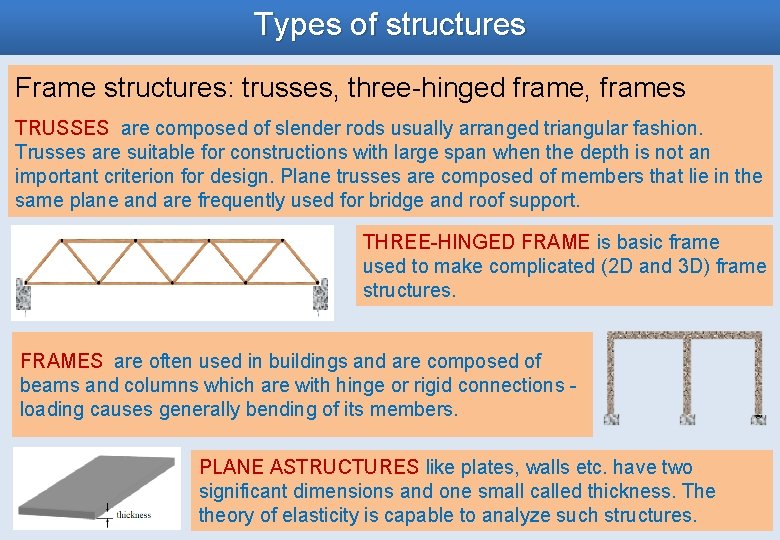
Types of structures Frame structures: trusses, three-hinged frame, frames TRUSSES are composed of slender rods usually arranged triangular fashion. Trusses are suitable for constructions with large span when the depth is not an important criterion for design. Plane trusses are composed of members that lie in the same plane and are frequently used for bridge and roof support. THREE-HINGED FRAME is basic frame used to make complicated (2 D and 3 D) frame structures. FRAMES are often used in buildings and are composed of beams and columns which are with hinge or rigid connections loading causes generally bending of its members. PLANE ASTRUCTURES like plates, walls etc. have two significant dimensions and one small called thickness. The theory of elasticity is capable to analyze such structures.

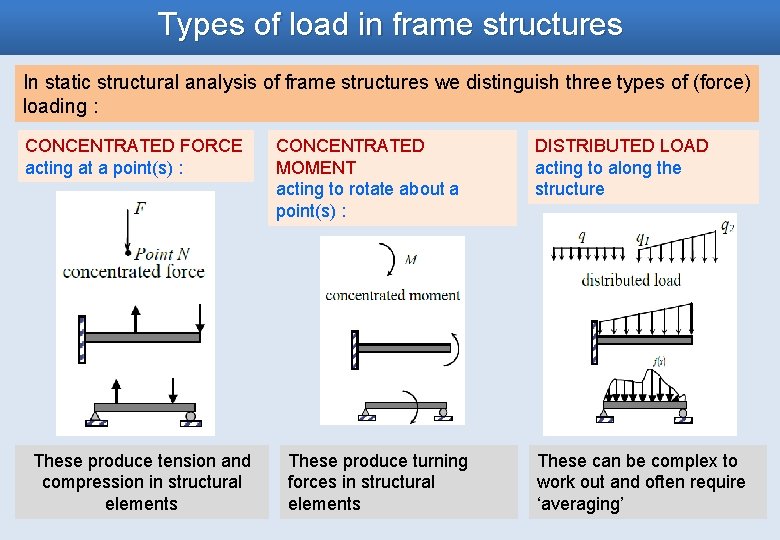
Types of load in frame structures In static structural analysis of frame structures we distinguish three types of (force) loading : CONCENTRATED FORCE acting at a point(s) : These produce tension and compression in structural elements CONCENTRATED MOMENT acting to rotate about a point(s) : These produce turning forces in structural elements DISTRIBUTED LOAD acting to along the structure These can be complex to work out and often require ‘averaging’

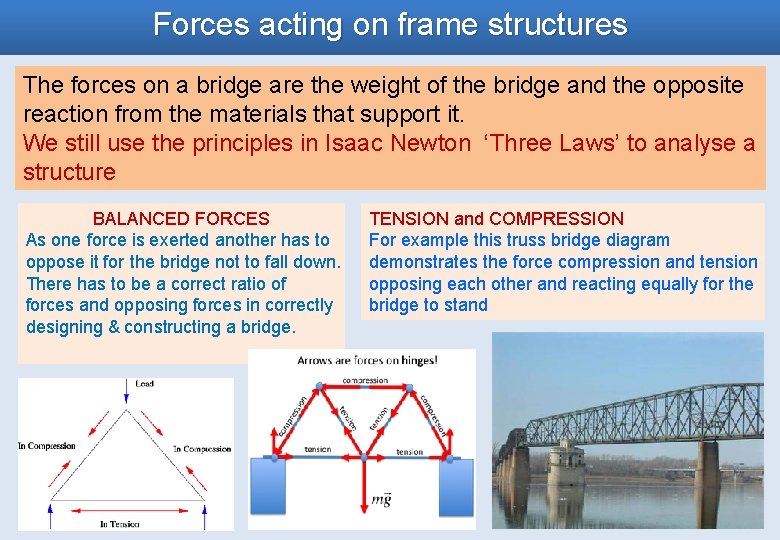
Forces acting on frame structures The forces on a bridge are the weight of the bridge and the opposite reaction from the materials that support it. We still use the principles in Isaac Newton ‘Three Laws’ to analyse a structure BALANCED FORCES As one force is exerted another has to oppose it for the bridge not to fall down. There has to be a correct ratio of forces and opposing forces in correctly designing & constructing a bridge. TENSION and COMPRESSION For example this truss bridge diagram demonstrates the force compression and tension opposing each other and reacting equally for the bridge to stand

Stress and strain Stress When a tensile force is applied to an object, the material will undergo stress – the force is spread out over the ‘cross-sectional area’ of the material STRESS describes the internal force acting within the material, and is defined as the force applied per unit area: F σ= A where: Area (A) Stress (σ) σ = stress in N/m 2 F = applied force in N A = area in m 2 Applied force (F)

Calculating stress Example Consider a steel bar with a cross-sectional area of 0. 005 m 2 that is subjected to a tensile force of 50 k. N. What is the stress on the material ? Answer in MN/m 2. 3 N 50 × 10 σ= 0. 005 m 2 F σ= A where: σ = stress in N/m 2 F = applied force in N A = area in m 2 σ = 10, 000 N/m 2 σ = 10 MN/m 2 Answer : 10 MN/m 2 Be careful in using the correct units

Strain is the change in shape of the material STRAIN is the ratio of the change in length to the original length. For a material undergoing tension, strain can be calculated as follows: ε= Δl l where: ε = strain l = original length in m Δl = extension in m Δl l

Calculating strain Example Consider a metal bar with an original length of 0. 2 m. Calculate the strain when it is subjected to a tensile force and the bar extends by 0. 02 m: ε = 0. 02 m 0. 2 m ε = 0. 1 Strain is a ratio; it does not have units. ε= Δl l 0. 02 m where: ε = strain l = original length in m Δl = extension in m 0. 2 m

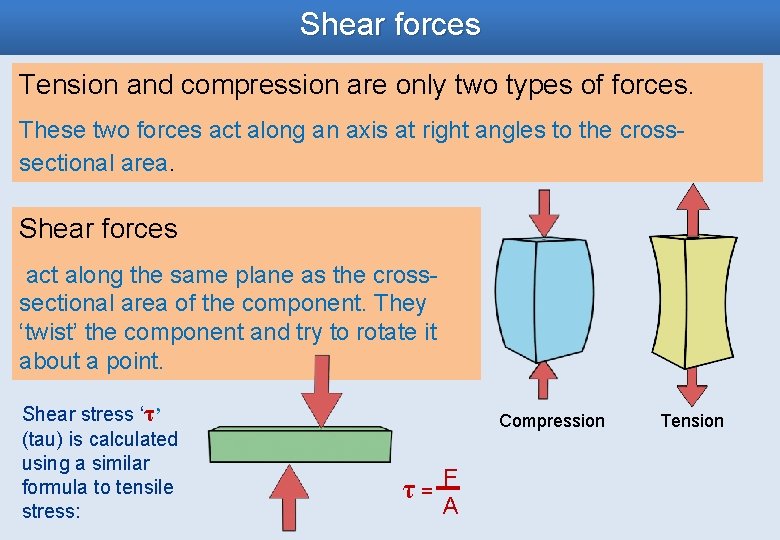
Shear forces Tension and compression are only two types of forces. These two forces act along an axis at right angles to the crosssectional area. Shear forces act along the same plane as the crosssectional area of the component. They ‘twist’ the component and try to rotate it about a point. Shear stress ‘τ’ (tau) is calculated using a similar formula to tensile stress: Compression τ= F A Tension

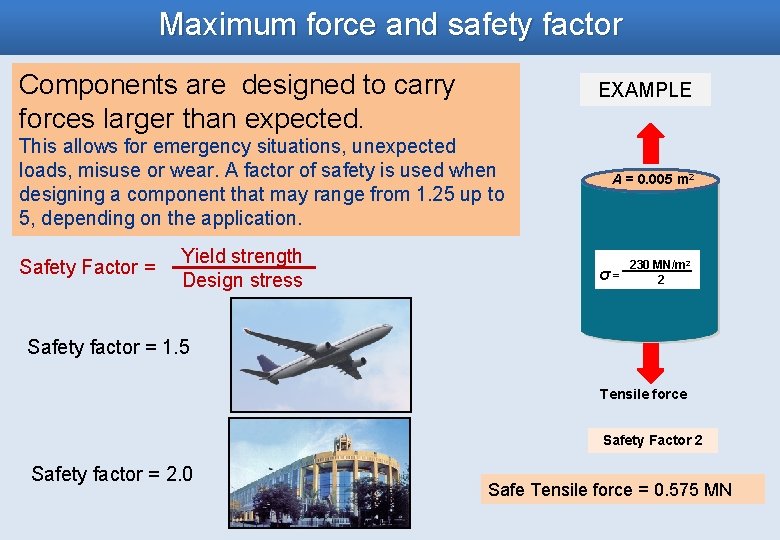
Maximum force and safety factor Components are designed to carry forces larger than expected. EXAMPLE This allows for emergency situations, unexpected loads, misuse or wear. A factor of safety is used when designing a component that may range from 1. 25 up to 5, depending on the application. Safety Factor = Yield strength Design stress A = 0. 005 m 2 σ= 230 MN/m 2 2 Safety factor = 1. 5 Tensile force Safety Factor 2 Safety factor = 2. 0 Safe Tensile force = 0. 575 MN

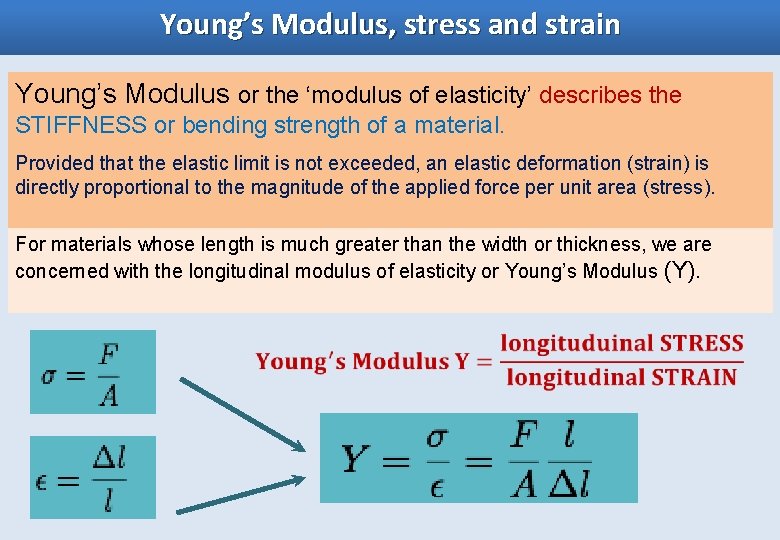
Young’s Modulus, stress and strain Young’s Modulus or the ‘modulus of elasticity’ describes the STIFFNESS or bending strength of a material. Provided that the elastic limit is not exceeded, an elastic deformation (strain) is directly proportional to the magnitude of the applied force per unit area (stress). For materials whose length is much greater than the width or thickness, we are concerned with the longitudinal modulus of elasticity or Young’s Modulus (Y).

Force, stress and strain with two bars in parallel Brief Intermission TWO bars in parallel, under the same force have the same STRAIN. What do you know about moments or torque ? For one bar made of material 1 : For other bar made of material 2 : If both bars have the SAME strain :

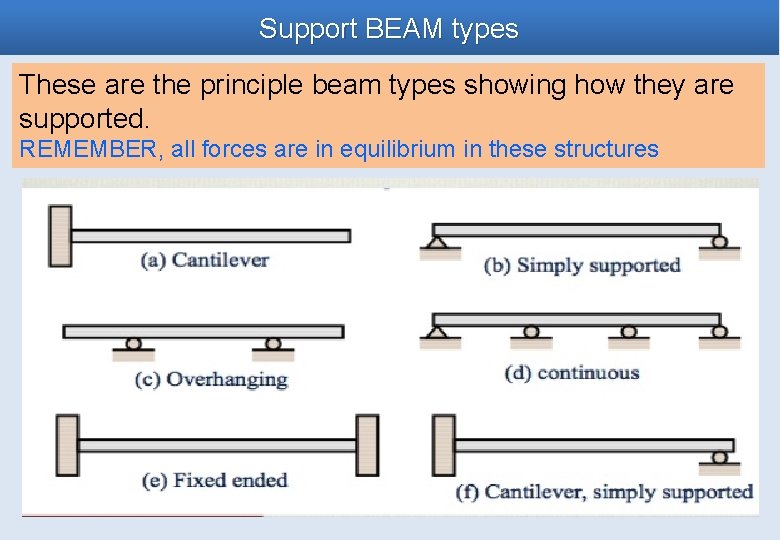
Support BEAM types These are the principle beam types showing how they are supported. REMEMBER, all forces are in equilibrium in these structures

Worked examples on the forces on a supported beam Check forces in the system You should look at the forces to resolve their components, examine vertical and horizontal components of those forces AND also examine turning forces (or moments) present in the system. REMEMBER, all these forces are in equilibrium. For a simply supported beams 1. SPLIT forces INTO COMPONENTS ( 3. SOLVE for MOMENTS in balance. total forces vectors = 0) Convert any forces at an angle to X and Y (vertical and horizontal) components. 2. MOMENTS are in EQUILIBRIUM. 4. SOLVE for VERTICAL FORCES EQUILIBRIUM. (total clockwise and anticlockwise moments = 0) Take moments about a joint or support 5. SOLVE for HORIZONTAL FORCES NOTE: Make sure you give a negative sign if EQUILIBRIUM. moment is anti-clockwise.

Worked examples on the forces on a supported beam Now apply it to this problem. REMEMBER all forces are in equilibrium. 1. Vertical and horizontal components Vertical only needed 8 k. N = Reaction A + Reaction B 2. Momentum equilibrium Take moments about A 0 = + (3 x 8) – (5 x. FB) 0 = clockwise mom. – anticlock mom. 3. Solve to find FB 5 x FB = 24 4. Vertical force equilibrium 0 = -8 + 4. 8 + FA FA FB = 4. 8 k. N FA = 3. 2 k. N

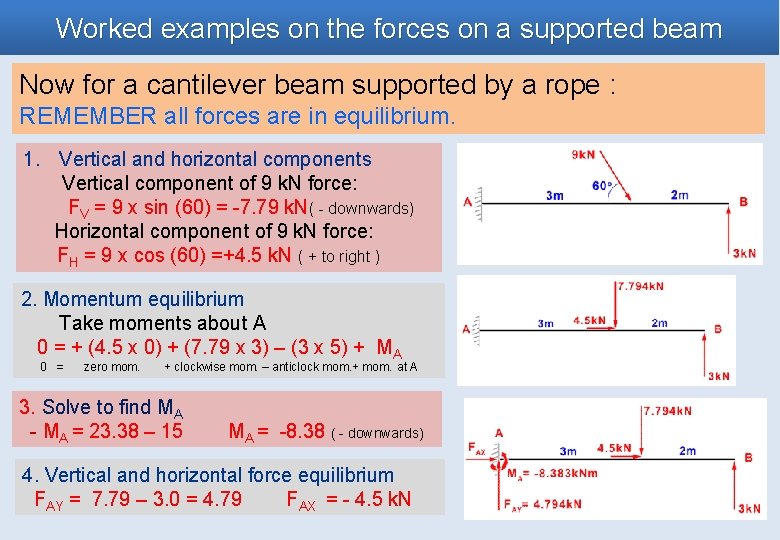
Worked examples on the forces on a supported beam Now for a cantilever beam supported by a rope : REMEMBER all forces are in equilibrium. 1. Vertical and horizontal components Vertical component of 9 k. N force: FV = 9 x sin (60) = -7. 79 k. N( - downwards) Horizontal component of 9 k. N force: FH = 9 x cos (60) =+4. 5 k. N ( + to right ) 2. Momentum equilibrium Take moments about A 0 = + (4. 5 x 0) + (7. 79 x 3) – (3 x 5) + MA 0 = zero mom. + clockwise mom. – anticlock mom. + mom. at A 3. Solve to find MA - MA = 23. 38 – 15 MA = -8. 38 ( - downwards) 4. Vertical and horizontal force equilibrium FAY = 7. 79 – 3. 0 = 4. 79 FAX = - 4. 5 k. N

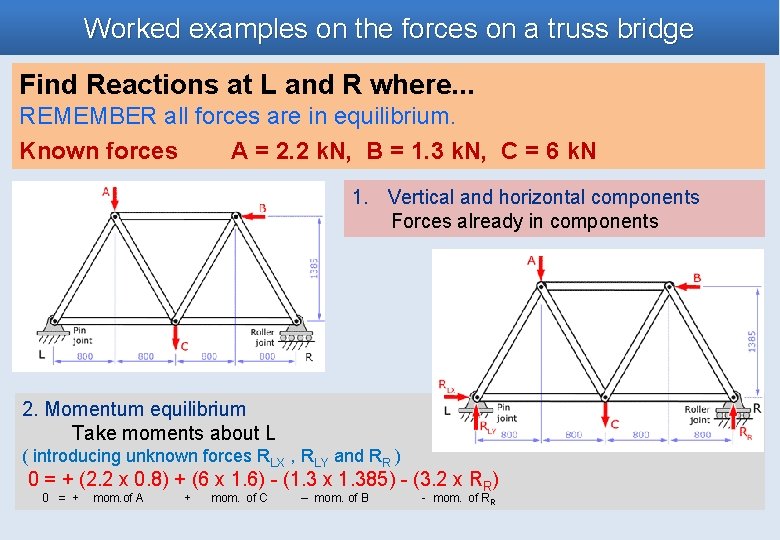
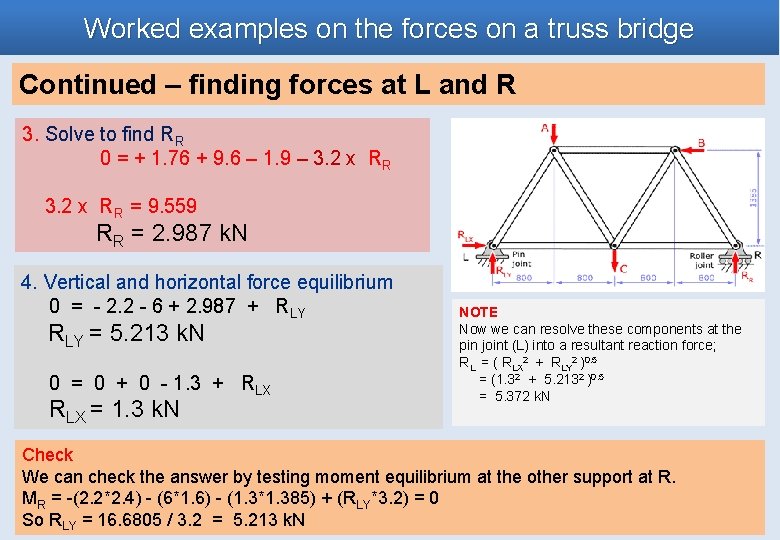
Worked examples on the forces on a truss bridge Find Reactions at L and R where. . . REMEMBER all forces are in equilibrium. Known forces A = 2. 2 k. N, B = 1. 3 k. N, C = 6 k. N 1. Vertical and horizontal components Forces already in components 2. Momentum equilibrium Take moments about L ( introducing unknown forces RLX , RLY and RR ) 0 = + (2. 2 x 0. 8) + (6 x 1. 6) - (1. 3 x 1. 385) - (3. 2 x RR) 0 = + mom. of A + mom. of C – mom. of B - mom. of RR

Worked examples on the forces on a truss bridge Continued – finding forces at L and R 3. Solve to find RR 0 = + 1. 76 + 9. 6 – 1. 9 – 3. 2 x RR = 9. 559 RR = 2. 987 k. N 4. Vertical and horizontal force equilibrium 0 = - 2. 2 - 6 + 2. 987 + RLY = 5. 213 k. N 0 = 0 + 0 - 1. 3 + RLX = 1. 3 k. N NOTE Now we can resolve these components at the pin joint (L) into a resultant reaction force; RL = ( RLX 2 + RLY 2 )0. 5 = (1. 32 + 5. 2132 )0. 5 = 5. 372 k. N Check We can check the answer by testing moment equilibrium at the other support at R. MR = -(2. 2*2. 4) - (6*1. 6) - (1. 3*1. 385) + (RLY*3. 2) = 0 So RLY = 16. 6805 / 3. 2 = 5. 213 k. N

How to find a Shear Force Diagram (SFD) of a Simple Beam To calculate the shear forces of a beam, follow the following simple steps: 1. Start with the far left side of the beam If there is an upward force (i. e a support) then the SFD will start at this force above the x-axis. If there is a downward point load and no support, than the shear force diagram will start as a negative at the value of the point load 2. Move across the beam As you come across loads, you simply add (or subtract) these loads from the value you already have, keeping a cumulative total. It is much easier to understand when considering an example of a how to calculate a Shear Force Diagram

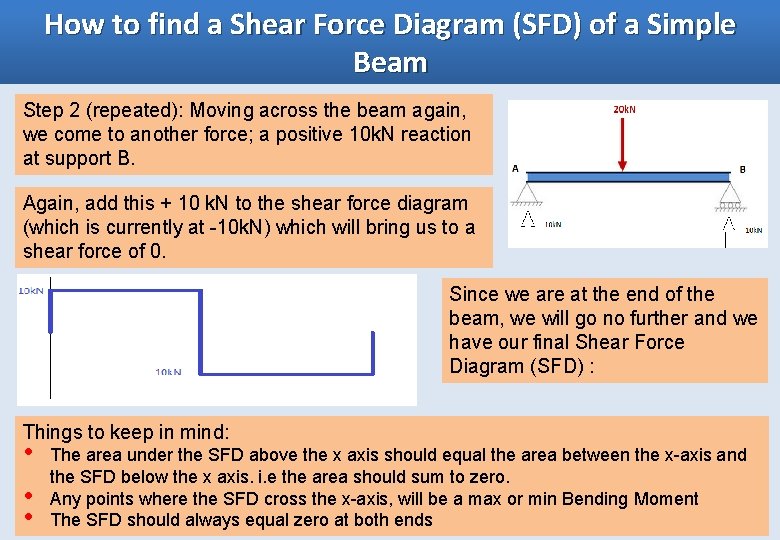
How to find a Shear Force Diagram (SFD) of a Simple Beam Step 1: After calculating the reactions at A and B, start the Shear Force Diagram at the first value of the force acting on the beam. In this case it is a +10 k. N due to the reaction at point A: Step 2: Keep moving across the beam, stopping at every load that acts on the beam. When you get to a load, add to the Shear Force Diagram by the amount of the force. In this case we have come to a negative 20 k. N force, so we will minus 20 k. N from the existing 10 k. N. i. e. 10 k. N 20 k. N = -10 k. N. Shear Force Diagram

How to find a Shear Force Diagram (SFD) of a Simple Beam Step 2 (repeated): Moving across the beam again, we come to another force; a positive 10 k. N reaction at support B. Again, add this + 10 k. N to the shear force diagram (which is currently at -10 k. N) which will bring us to a shear force of 0. Since we are at the end of the beam, we will go no further and we have our final Shear Force Diagram (SFD) : Things to keep in mind: • • • The area under the SFD above the x axis should equal the area between the x-axis and the SFD below the x axis. i. e the area should sum to zero. Any points where the SFD cross the x-axis, will be a max or min Bending Moment The SFD should always equal zero at both ends

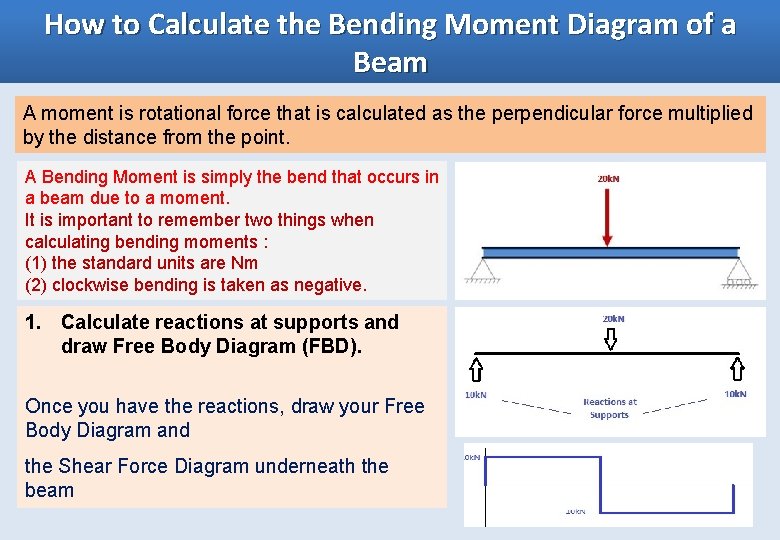
How to Calculate the Bending Moment Diagram of a Beam A moment is rotational force that is calculated as the perpendicular force multiplied by the distance from the point. A Bending Moment is simply the bend that occurs in a beam due to a moment. It is important to remember two things when calculating bending moments : (1) the standard units are Nm (2) clockwise bending is taken as negative. 1. Calculate reactions at supports and draw Free Body Diagram (FBD). Once you have the reactions, draw your Free Body Diagram and the Shear Force Diagram underneath the beam

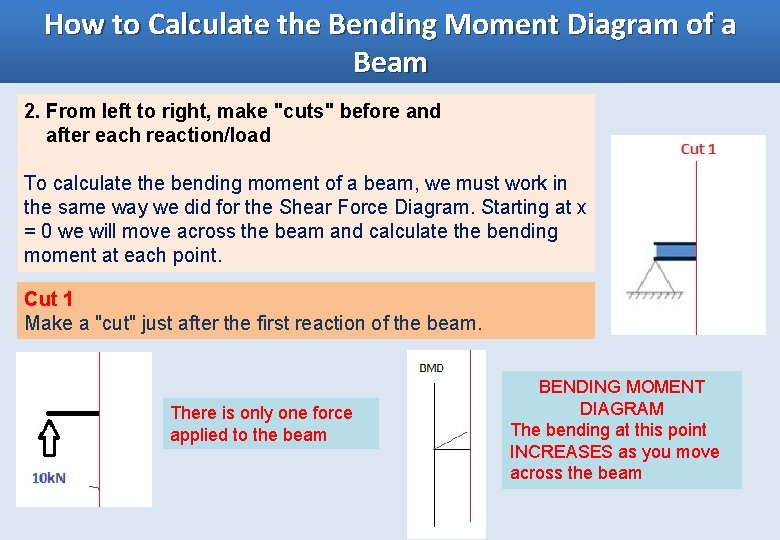
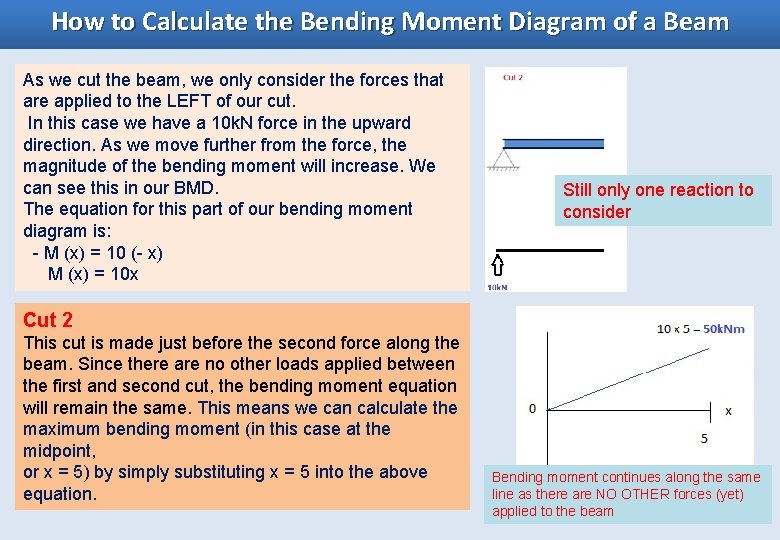
How to Calculate the Bending Moment Diagram of a Beam 2. From left to right, make "cuts" before and after each reaction/load To calculate the bending moment of a beam, we must work in the same way we did for the Shear Force Diagram. Starting at x = 0 we will move across the beam and calculate the bending moment at each point. Cut 1 Make a "cut" just after the first reaction of the beam. There is only one force applied to the beam BENDING MOMENT DIAGRAM The bending at this point INCREASES as you move across the beam

How to Calculate the Bending Moment Diagram of a Beam As we cut the beam, we only consider the forces that are applied to the LEFT of our cut. In this case we have a 10 k. N force in the upward direction. As we move further from the force, the magnitude of the bending moment will increase. We can see this in our BMD. The equation for this part of our bending moment diagram is: - M (x) = 10 (- x) M (x) = 10 x Still only one reaction to consider Cut 2 This cut is made just before the second force along the beam. Since there are no other loads applied between the first and second cut, the bending moment equation will remain the same. This means we can calculate the maximum bending moment (in this case at the midpoint, or x = 5) by simply substituting x = 5 into the above equation. Bending moment continues along the same line as there are NO OTHER forces (yet) applied to the beam

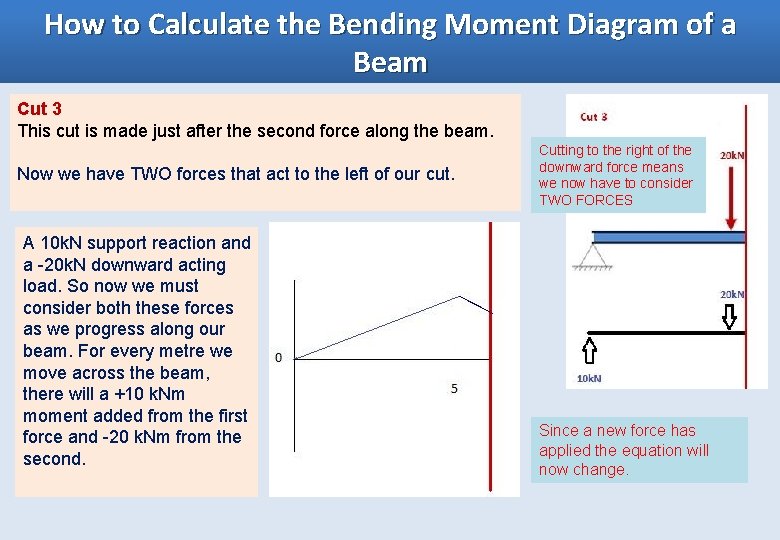
How to Calculate the Bending Moment Diagram of a Beam Cut 3 This cut is made just after the second force along the beam. Now we have TWO forces that act to the left of our cut. A 10 k. N support reaction and a -20 k. N downward acting load. So now we must consider both these forces as we progress along our beam. For every metre we move across the beam, there will a +10 k. Nm moment added from the first force and -20 k. Nm from the second. Cutting to the right of the downward force means we now have to consider TWO FORCES Since a new force has applied the equation will now change.

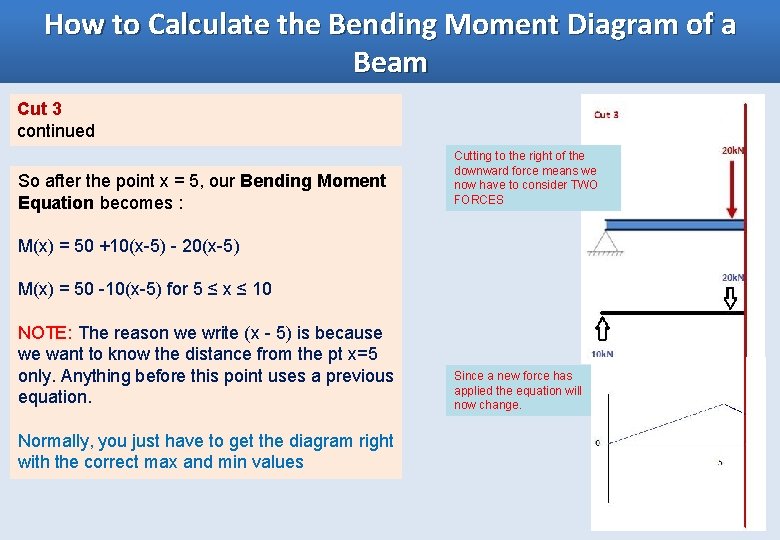
How to Calculate the Bending Moment Diagram of a Beam Cut 3 continued So after the point x = 5, our Bending Moment Equation becomes : Cutting to the right of the downward force means we now have to consider TWO FORCES M(x) = 50 +10(x-5) - 20(x-5) M(x) = 50 -10(x-5) for 5 ≤ x ≤ 10 NOTE: The reason we write (x - 5) is because we want to know the distance from the pt x=5 only. Anything before this point uses a previous equation. Normally, you just have to get the diagram right with the correct max and min values Since a new force has applied the equation will now change.

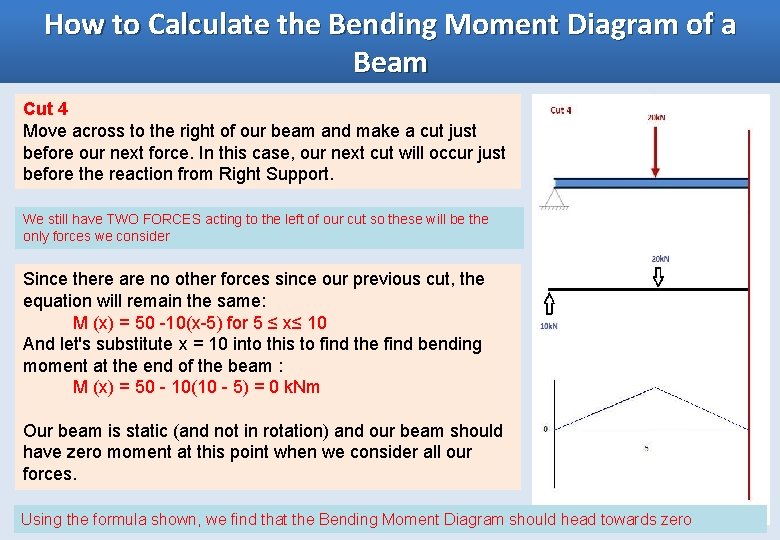
How to Calculate the Bending Moment Diagram of a Beam Cut 4 Move across to the right of our beam and make a cut just before our next force. In this case, our next cut will occur just before the reaction from Right Support. We still have TWO FORCES acting to the left of our cut so these will be the only forces we consider Since there are no other forces since our previous cut, the equation will remain the same: M (x) = 50 -10(x-5) for 5 ≤ x≤ 10 And let's substitute x = 10 into this to find the find bending moment at the end of the beam : M (x) = 50 - 10(10 - 5) = 0 k. Nm Our beam is static (and not in rotation) and our beam should have zero moment at this point when we consider all our forces. Using the formula shown, we find that the Bending Moment Diagram should head towards zero

Complete the review assessment EVALUATE your knowledge of engineering structures Knowledge Assessments ET 005 E and ET 005 F

Thank You Any Questions? If you need to contact me, please use: E-mail: a. wright@lowestoft. ac. uk Next week we will be looking at kinetic and potential energy and the effect of heat on materials and gases