Dynamic Programming Dynamic Programing A technique for designing

Dynamic Programming

Dynamic Programing • A technique for designing (optimizing) algorithms • It can be applied to problems that can be decomposed in subproblems, but these subproblems overlap. Instead of solving the same subproblems repeatedly, applying dynamic programming techniques helps to solve each subproblem just once.

Dynamic Programming Examples • • Fibonacci numbers Knapsack Maximum Consecutive Subsequence Longest Common Subsequence

Fibonacci numbers – Simple Recursive Solution Function Rec. Fibo(n) is: if (n<2) return n else return Rec. Fibo(n-1)+Rec. Fibo(n-2) T(n)=1, n<2 T(n-1)+T(n-2), n>=2 T(n)=O(2^n)

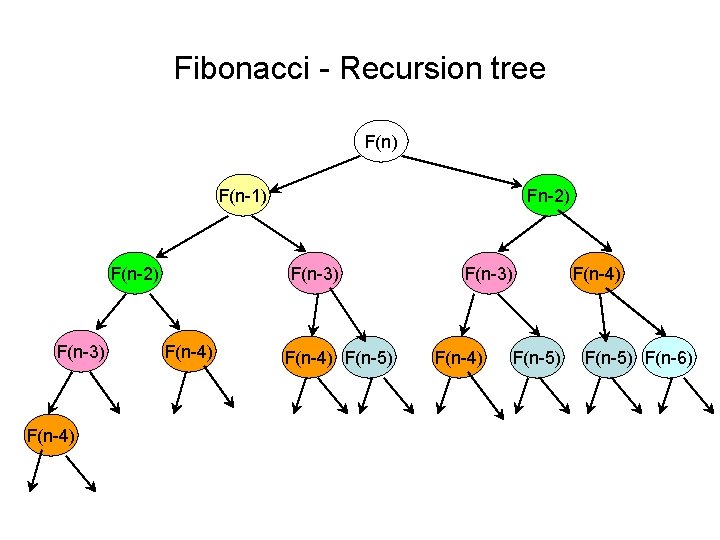
Fibonacci - Recursion tree F(n) F(n-1) F(n-2) F(n-3) F(n-4) F(n-5) F(n-3) F(n-4) F(n-5) F(n-6)

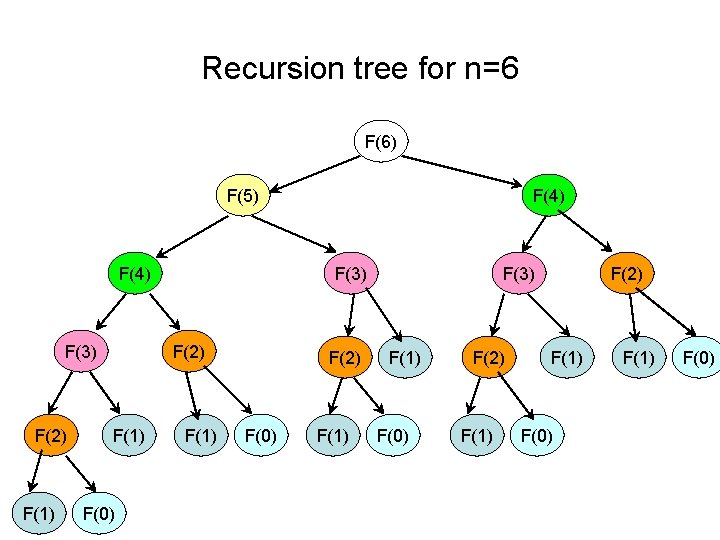
Recursion tree for n=6 F(6) F(5) F(4) F(3) F(2) F(1) F(0) F(4) F(1) F(2) F(0) F(1) F(3) F(1) F(0) F(2) F(1) F(0)

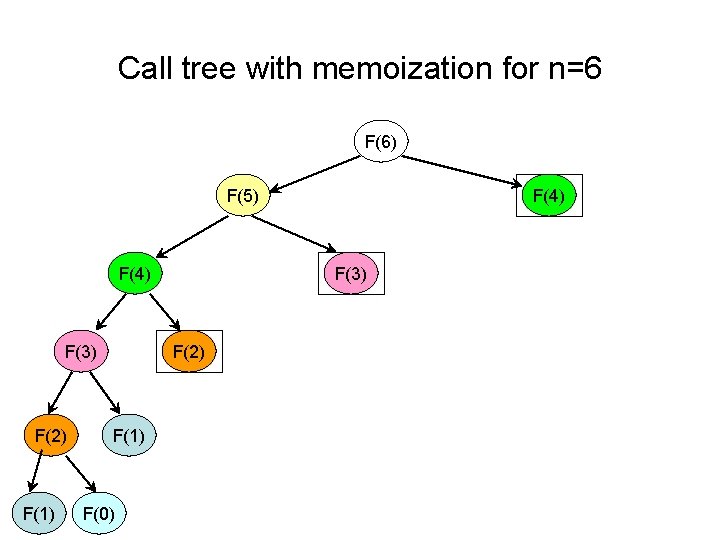
Fibonacci with memoization • We can speed up a recursive algorithm by writing down the results of the recursive calls and looking them up again if we need them later. This process was called memoization Function Mem. Fibo(n) is: if (n<2) return n else If (not F[n]. done) F[n]. value=Mem. Fibo(n-1)+Mem. Fibo(n-2) F[n]. done=true return F[n]. value Mem. Fibo computes n values of the array F[] => O(n)

Call tree with memoization for n=6 F(6) F(5) F(4) F(3) F(2) F(1) F(0) F(4)

Fibonacci - Dynamic programming solution • Look at the recursion tree to see in which order are filled the elements of array F[] – Elements of F[] are filled bottom-up (first F[2], F[3], … up to F[n]). • Replace the recursion with an iterative loop that intentionally fills the array in the right order Function Iter. Fibo(n) is: F[0]=0 F[1] =1 for i=2 to n do F[i]=F[i-1]+F[i-2] return F[n]

Fibonacci – improved memory complexity • In many dynamic programming algorithms, it may be not necessary to retain all intermediate results through the entire computation. • in step i of Fibonacci, we need only numbers F[i-1] and F[i-2] Function Iter. Fibo 2(n) is: prev=0 curr =1 for i=2 to n do next = prev + curr prev = curr = next return curr

Dynamic programming - Terminology • Memoization (not memorization!): the term comes from memo (memorandum), since the technique consists of recording a value so that we can look it up later. • Dynamic programming: The term was introduced in the 1950 s by Richard Bellman developed methods for constructing training and logistics schedules for the air forces, or as they called them, ‘programs’. The word ‘dynamic’ is meant to suggest that the table is filled in over time, rather than all at once • Dynamic programming as an algorithm design method comprises several optimization levels: 1. Eliminate redundand work on identical subproblems – use a table to store results (memoization) 2. Eliminate recursivity – find out the order in which the elements of the table have to be computed (dynamic programming) 3. Reduce memory complexity if possible

The Integer Exact Knapsack • The problem: Given an integer K and n items of different sizes such that the i’th item has an integer size[i], determine if there is a subset of the items whose sizes sum to exactly K, or determine that no such subset exist • Example: n=4, sizes={2, 3, 5, 6}, K=7 – Greedy will not work ! • P(n, K) – the problem for n items and a knapsack of K • P(i, k) – the problem for the first i<=n items and a knapsack of size k<=K

The Integer Exact Knapsack (n, K) is If n=1 if size[n]=K return true else return false If Knapsack(n-1, K)=true return true else if size[n]=K return true else if K-size[n]>0 return Knapsack(n-1, K-size[n]) else return false T(n)= 2*T(n-1)+c, n>2 T(n)=O(2^n)

Knapsack - Recursion tree F(n, K) F(n-1, K) F(n-2, K-s[n-1]) F(n-1, K-s[n]) F(n-2, K-s[n]-s[n-1]) Number of nodes in recursion tree is O(2 n) Max number of distinct function calls F(i, k), where i in [1, n] and k in [1. . K] is n*K F(i, k) returns true if we can fill a sack with size k from the first i items If 2 n >n*K, it is sure that we have 2 n-n*K calls repeated We cannot identify the duplicated nodes in general, they depend on the values of size ! Even if 2 n<n*K, it is possible to have repeated calls, but it depends on the values of size[]

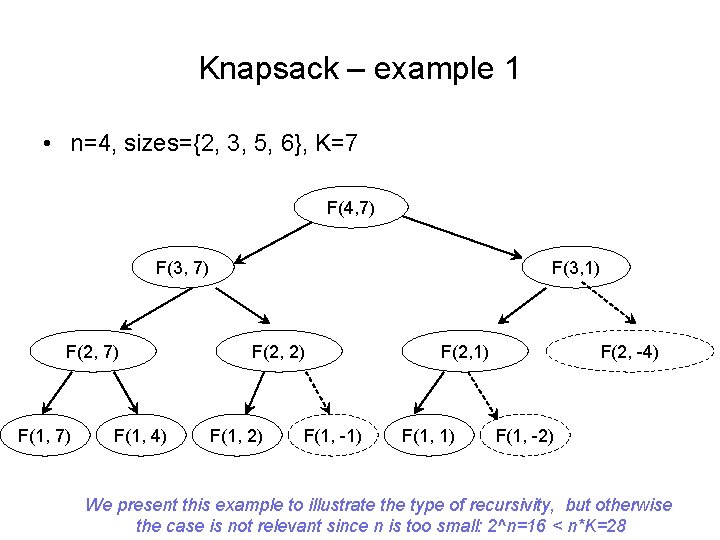
Knapsack – example 1 • n=4, sizes={2, 3, 5, 6}, K=7 F(4, 7) F(3, 7) F(2, 7) F(1, 4) F(3, 1) F(2, 2) F(1, -1) F(2, 1) F(1, 1) F(2, -4) F(1, -2) We present this example to illustrate the type of recursivity, but otherwise the case is not relevant since n is too small: 2^n=16 < n*K=28

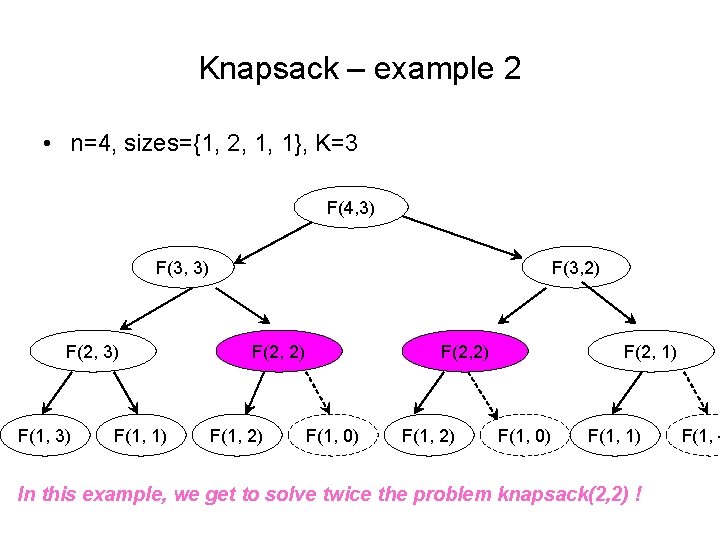
Knapsack – example 2 • n=4, sizes={1, 2, 1, 1}, K=3 F(4, 3) F(3, 3) F(2, 3) F(1, 1) F(3, 2) F(2, 2) F(1, 0) F(1, 2) F(2, 1) F(1, 0) F(1, 1) In this example, we get to solve twice the problem knapsack(2, 2) ! F(1, -

Knapsack – Memoization • Memoization: We use a table P with n*K elements, where P[i, k] is a record with 2 fields: – Done: a boolean that is true if the subproblem (i, k) has been computed before – Result: used to save the result of subproblem (i, k) • Implementation: in the recursive function presented before, replace every recursive call of Knapsack(x, y) with a sequence like If P[x, y]. done …. P[x, y]. result //use stored result Else P[x, y]. result=Knapsack(x, y) //compute and store P[x, y]. done=true

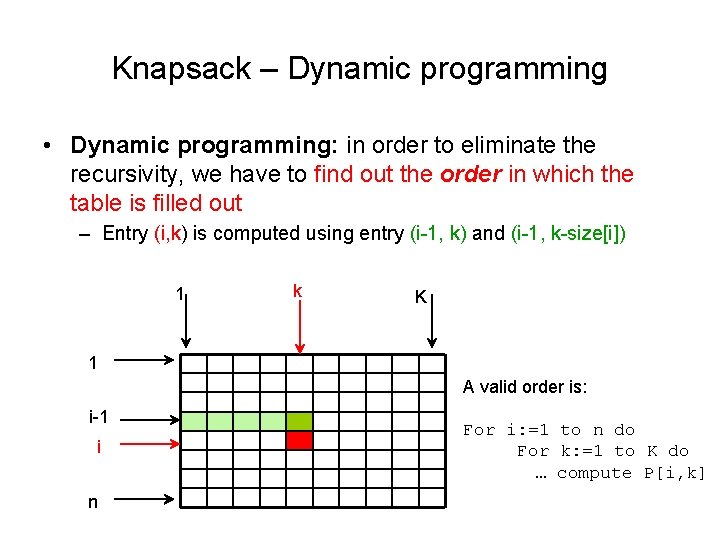
Knapsack – Dynamic programming • Dynamic programming: in order to eliminate the recursivity, we have to find out the order in which the table is filled out – Entry (i, k) is computed using entry (i-1, k) and (i-1, k-size[i]) 1 k K 1 A valid order is: i-1 i n For i: =1 to n do For k: =1 to K do … compute P[i, k]

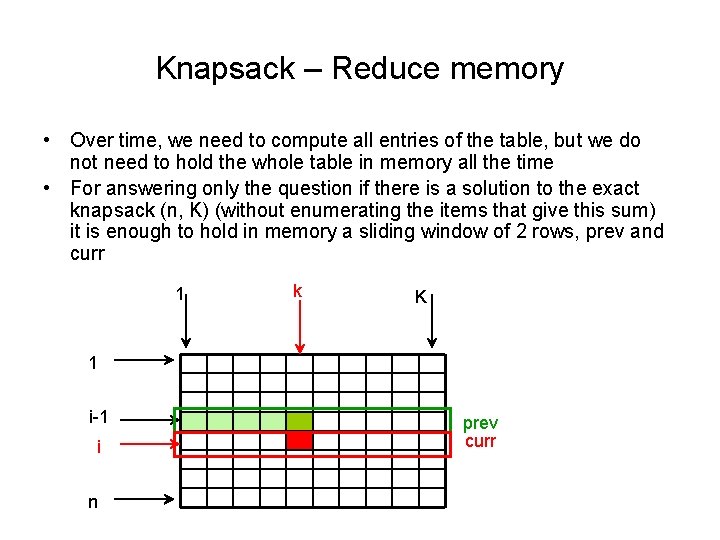
Knapsack – Reduce memory • Over time, we need to compute all entries of the table, but we do not need to hold the whole table in memory all the time • For answering only the question if there is a solution to the exact knapsack (n, K) (without enumerating the items that give this sum) it is enough to hold in memory a sliding window of 2 rows, prev and curr 1 k K 1 i-1 i n prev curr

Knapsack – determine also the set of items • If we are also interested in finding the actual subset that fits in the knapsack, then we can add to the table entry a flag that indicates whether the corresponding item has been selected in that step • This flag can be traced back from the last entry which is (n, K) and the subset can be recovered • In this case, we cannot reduce the memory complexity, we need the full table (n, K) !

Finding the Maximum Consecutive Subsequence • Problem: Given a sequence X = (x 1, x 2, …, xn) of (not necessarily positive) real numbers, find a subsequence xi; xi+1; … ; xj of consecutive elements such that the sum of the numbers in it is maximum over all subsequences of consecutive elements • Example: The profit history (in billion $) of the company Prod. Inc. Corp for the last 10 years is given below. Find the maximum amount that Prod. Inc. Corp earned in any contiguous span of years. y 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 y 10 2 -3 1. 5 -1 3 -2 0. 5 1 -2

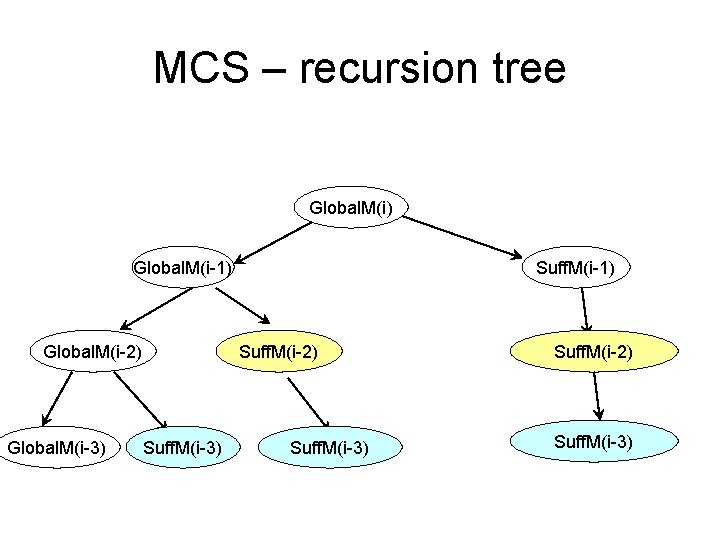
MCS - recursive • Global. M(i)=max(Global. M(i-1), Suff. M(i-1)+xi) • Suff. M(i)=max(0, Suff. M(i-1)+xi)

MCS – recursion tree Global. M(i) Global. M(i-1) Global. M(i-2) Global. M(i-3) Suff. M(i-1) Suff. M(i-2) Suff. M(i-3)

MCS - Solution Algorithm Max_Subsequence(X, n) Input: X (array of length n) Output: Global_Max (The sum of the maximum subsequence) begin Global_Max: = 0; Suffix_Max : = 0; for i=1 to n do if x[i] + Suffix_Max > Global_Max then Suffix_Max : = Suffix. Max + x[i]; Global_Max : = Suffix_Max; else if x[i] + Suffix_Max > 0 then Suffix_Max : = Suffix_Max + x[i]; else Suffix_Max : = 0; end

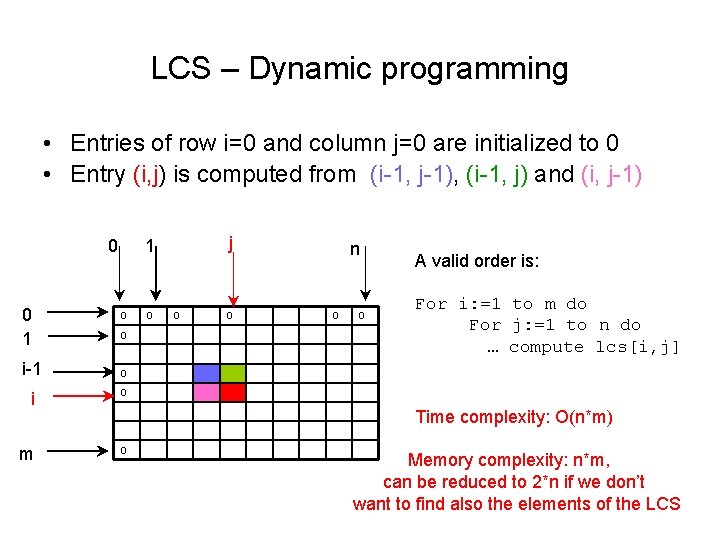
The Longest Common Subsequence • Given 2 sequences, X ={x 1; : : : ; xm} and Y ={y 1; : : : ; yn}. Find a subsequence common to both whose length is longest. A subsequence doesn’t have to be consecutive, but it has to be in order. HORSEBACK LCS = OAK SNOWFLAKE

LCS • • • X = {x 1, … xm} Y = {y 1, …, yn} Xi = the prefix subsequence {x 1, … xi} Yi = the prefix subsequence {y 1, … yi} Z ={z 1, … zk} is a LCS of X and Y. LCS(i, j) = LCS of Xi and Yj LCS(i, j) = 0, if i=0 or j=0 LCS(i-1, j-1)+1, if xi=yj max(LCS(i, j-1), LCS(i-1, j)), if xi<>yj See [CLRS] – chap 15. 4

LCS – Dynamic programming • Entries of row i=0 and column j=0 are initialized to 0 • Entry (i, j) is computed from (i-1, j-1), (i-1, j) and (i, j-1) 0 0 1 i-1 j 1 0 0 0 n 0 0 A valid order is: For i: =1 to m do For j: =1 to n do … compute lcs[i, j] 0 i 0 m 0 Time complexity: O(n*m) Memory complexity: n*m, can be reduced to 2*n if we don’t want to find also the elements of the LCS

LCS - applications • Molecular biology – DNA sequences (genes) can be represented as sequences of submolecules, each of these being one of the four types: A C G T. In genetics, it is of interest to compute similarities between two DNA sequences by LCS • File comparison – Versioning systems: example - "diff" is used to compare two different versions of the same file, to determine what changes have been made to the file. It works by finding a LCS of the lines of the two files;

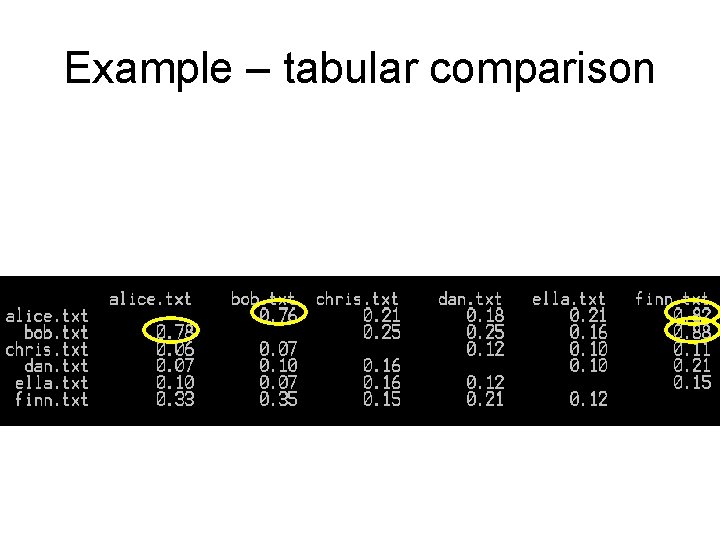
Project • A plagiarism detection tool based on the LCS algo • The tools takes arguments in the command line, and depending on these arguments it can function in one of the following two modes: – Pair comparison mode: -p file 1 file 2 – In pair comparison mode, the tool takes as arguments the names of two text files and displays the content found to be identical in the two files. – Tabular mode: -t dirname – In tabular mode, the tool takes as argument the name of a directory and produces a table containing for each pair of distinct files (file 1, file 2) the percentage of the contents of file 1 which can be found also in file 2.

Example – It seems easy … I have a pet dog. His name is Bruno. His body is covered with bushy white fur. He has four legs and two beautiful eyes. My dog is the best dog one can ever have. I have a cat. His name is Paw. His body is covered with shiny black fur. He has four legs and two yellow eyes. My cat is the best cat one can ever have. LCS/File length: 133/168=0. 80 133/167=0. 79

Example – tabular comparison

But, in practice … • Problem 1: Size – Size of files: an essay of 20000 words has approx 150 KB – m*n approx 20 GB !!! Memory needed for storing a table – m*n iterations => long running time • Problem 2: Quality of detection results – Applying LCS on strings of characters may lead to false positive results if one file is much shorter than the other – Applying LCS on lines (as diff does) may lead to false negative results due to simple text formatting with different margin sizes

Project – practical challenge • Implement a plagiarism detection tool based on the LCS algorithm • Requirements: – Analyze essays of up to 20000 words in no more than a couple of minutes – Doesn’t crash in tabular mode for essays of 100. 000 words – Produce good detection results under following usage assumptions: • Detects the similar text even if: – Some text parts have been added, changed or removed – The text has been formatted differently • More details + test data: • http: //bigfoot. cs. upt. ro/~ioana/algo/lcs_plag. html

Project – practical challenge • Project is optional, but: – Submitting a complete and good project in time brings 1 award point ! • Hard deadline for this: Monday, 24. 03. 2014, 10: 00 am, by e-mail to ioana. sora@cs. upt. ro – Doing the project later and presenting it during the lab classes (but not later than 2 weeks) will bring you some credit for the lab grade