Decisions under Ignorance Last Time Last time we



































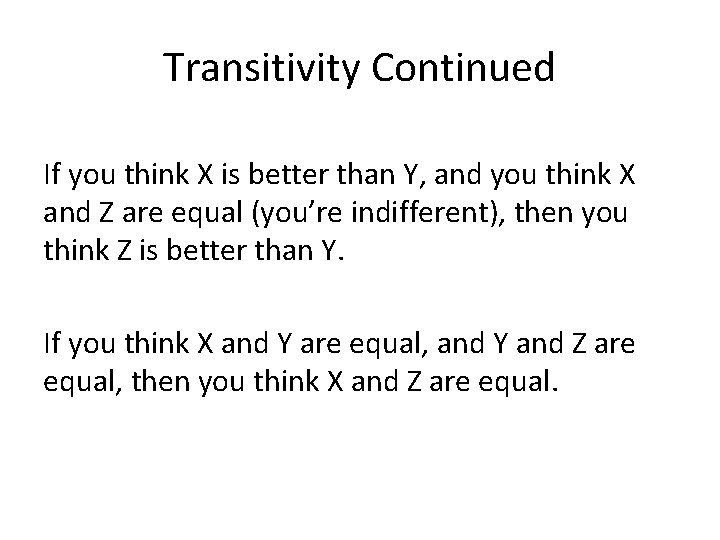





















- Slides: 64

Decisions under Ignorance

Last Time Last time we introduced decision theory, the scientific/ philosophical study of how best to make your decisions, given what your goals and aspirations are.

Problem Specification Solving a decision problem begins with a problem specification, breaking down the problem into three components: 1. Acts: the various (relevant) actions you can take in the situation. 2. States: the different ways that things might turn out (coin lands heads, coin lands tails). 3. Outcomes: What results from the various acts in the different states.

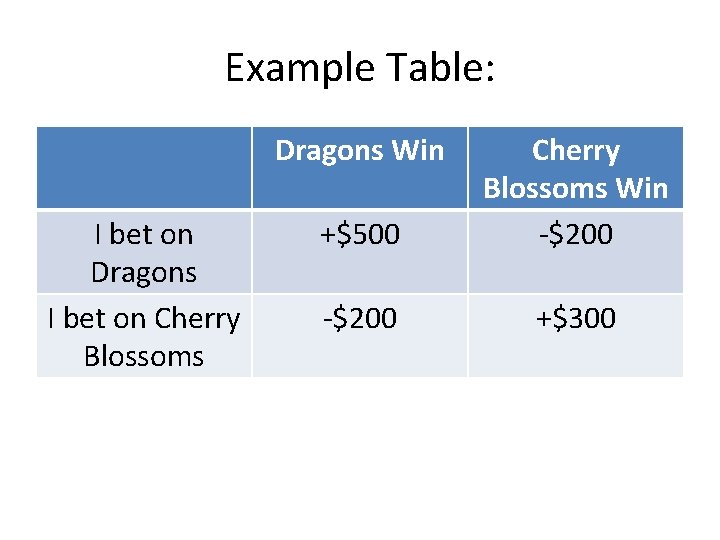
Example For example, we considered a simple decision problem involved in betting on a sports team: 1. Acts: Bet on the Dragons, bet on the Cherry blossoms. 2. States: Dragons win, Cherry Blossoms win. 3. Outcomes: +$500 for successful bet on Dragons, +$300 for successful bet on Cherry Blossoms, -$200 for any lost bet.

Decision Tables Decisions, after being analyzed by a problem specification, can be summarized in a decision table, with the Acts on the left, the States on the top, and the corresponding Outcomes for each Act, State pair in their appropriate locations.

Example Table: Dragons Win I bet on Dragons I bet on Cherry Blossoms +$500 Cherry Blossoms Win -$200 +$300

Independence of States on Acts One important feature we learned about was that the states we specify must not depend on which actions we take. For instance, the state “I win” depends on whether I bet on the Dragons or the Cherry Blossoms. When states depend on acts, we run the risk of incorrectly solving the decision problem.

Immediate Choices When we make a decision table, we have to make choices about how to describe the acts and states. And obviously decision theory can’t help us with those choices. It can’t help us with a lot of choices: if a bear is chasing you, you don’t need or want a decision table to make a choice to run away. But for more difficult problems that require advance planning, decision theory can be useful.

Right Choice vs. Rational Choice Decision theory is not concerned with making the right choice– it’s concerned with making the rational choice when you don’t know what the right choice is. The right choice is the choice that gets you the best outcome. If you are betting on sports, you typically won’t know what the right choice is (who will win). Sometimes the rational choice can still be the wrong choice.

Varieties of Decisions Decision theorists classify decisions into three categories: 1. Decisions under certainty 2. Decisions under risk 3. Decisions under ignorance

Decisions under Certainty Sometimes you know for certain what outcome an act will have. At a restaurant you are faced with a decision: do I order the soup or the salad? You know that if you order the soup, the outcome will be that you get soup, and if you order the salad, the outcome will be that you get salad. Any decision where all the acts are like this– you know their outcomes in advance– is a decision under certainty.

Hard Decisions Just because a decision is made under certainty does not mean it is an easy or obvious decision. Deciding which classes to take is a decision under certainty (often): you get what you sign up for. But should you take philosophy this semester or music? That can be a difficult decision.

Formal Approaches We won’t be talking about decisions under certainty in this class. There are formal approaches to these problems (for example, in the mathematics of linear programming), but that’s a little bit out of our range.

Decisions under Risk Sometimes it is possible to assign determinate (or approximate) probabilities to various states. For example, when I flip a fair coin, I know that the probability that it lands heads will be 0. 5 and the probability that it lands tails will be 0. 5. So if I bet on a fair coin (or an unfair coin, when I know its probabilities) that is a decision under risk.

Idealization A lot of things are very difficult to assign exact probabilities to, but that doesn’t mean they shouldn’t be treated as decisions under risk. Sometimes confronting a problem requires idealization. You don’t know exactly the probability that your plane flight will crash, but you can estimate it by considering the number of crashes divided by the number of flights.

Next Week Next week we’ll talk about decisions under risk. They require a little bit more of a mathematical approach. The general idea is to calculate which outcome we expect to happen given each of our acts, and then to choose the act that has the best expected outcome.

Decisions under Ignorance A large number of decisions are decisions under ignorance (also known as a decision under uncertainty). These are decisions where we cannot assign probabilities to some of the states, or where our estimates are too wide (“somewhere between a 20% and 80% chance”).

Example For example, suppose you go on a first date with someone. What is the probability that you will wind up getting married to them and subsequently having children and grandchildren with them? You certainly can’t get an estimate by dividing your total number of marriages by your total number of first dates– you probably don’t have a very high number of either.

Example So suppose your friend calls you and asks if you want to go see the new James Bond movie instead of going on this date. You really want grandchildren someday, but you can’t assign a probability to the state that you will have grandchildren with your date. This is a decision under ignorance.

Second Example Suppose that Susan is starting her career in business. She has been very successful so far, and has made lots of contacts, and thinks that if she keeps at it, she will be able to become very rich.

Susan’s Choice Susan is recently married, and she wants to have children some day. She is faced with the following decision: should she have children now and postpone her career, or should she keep on the successful track she’s on and have children later? She knows whatever she does now she’ll be good at, but she doesn’t know what she’ll be good at later.

Decision under Ignorance Susan has read a lot of parenting books and studies done on parenting late in life, so she is pretty confident that she can assign a probability to being a good parent later vs. now. However, she has no idea whether she will be able to resume a successful business career after staying home for years to raise her children. She cannot assign that state a probability, so this is a decision under ignorance.

Note [Note: I’m not saying that women have to stay home when they have children. Susan just happens to be conservative, and she thinks that women should not work when their children are young. As decision theorists, we don’t judge what other people’s goals are, we just help them make the best decisions to achieve those goals. ]

Acts The acts here are clear: A 1: Susan has children now, and a career later. A 2: Susan has a career now, and children later.

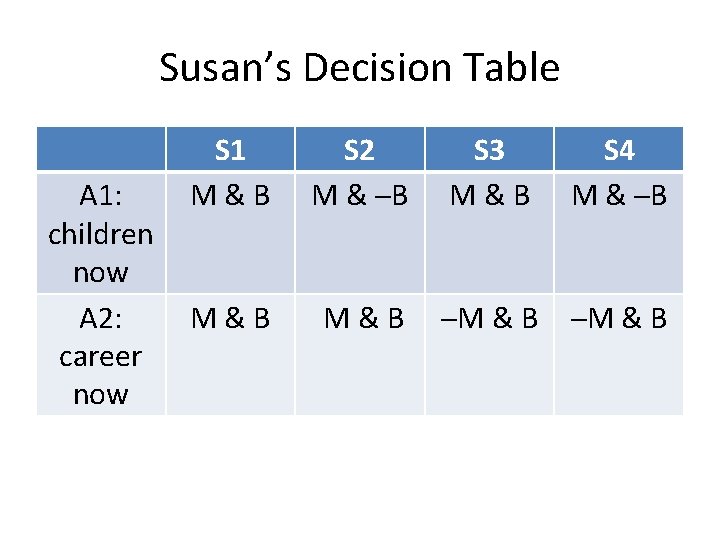
Relevant States S 1: In 7 years, Susan will be able to be both a good mother and a good businesswoman. S 2: In 7 years, she will be able to be a good mother, but not a good businesswoman. S 3: In 7 years, she will not be able to be a good mother, but she will be able to be a good businesswoman. S 4: In 7 years, she will neither be able to be a good mother nor a good businesswoman.

Outcomes The outcome for each act-state pair is pretty clear here. For example, for A 2 and S 1: A 2: Susan has a career now, and children later. S 1: In 7 years, she will be able to be a good mother but not able to be a good businesswoman. O 1: She is a good mother later and a good businesswoman now.

It will be easier if we can summarize things as follows: M = Susan is a good mother. ─M = Susan is not a good mother. B = Susan is a good businesswoman. ─B = Susan is not a good businesswoman.

Susan’s Decision Table A 1: children now A 2: career now S 1 M&B S 2 M & ─B S 3 M&B S 4 M & ─B M&B ─M & B

Preferences How is Susan going to make this decision. Well, first, a decision theorist needs to know her preferences. Which outcomes does she prefer to which other outcomes. For example, clearly Susan prefers M & B to ─M & B: she prefers being a good mother and having a good career to just being a bad mother and having a good career.

Preferences But what about what happens in S 4: if she chooses children now, she’ll be a good mother, but not a good businesswoman (M & ─B). If she chooses a career now, she’ll be a good businesswoman, but not a good mother (─M & B). Which of these two does she prefer, being only a good mother or only a good businesswoman?

Indifference Susan might have a definite preference, but we also allow her to be indifferent: she might think that (M & ─B) and (─M & B) are equally good outcomes, and she would be equally happy with either of them.

Rational Preferences We’re still not in a position to help Susan. In order to help her, the decision theorist requires that her preferences be rational. Rationality here has nothing to do with which things she prefers. It’s OK if she prefers ─M & ─B to M & B. That would be strange, but it’s not irrational.

Rational Preferences Rational preferences have the following features: 1. They are connected. 2. They are (appropriately) asymmetrical. 3. They are transitive.

Connected Your preferences for outcomes O 1, O 2, O 3, … are connected if, for any two of those outcomes X and Y: Either you prefer X to Y Or you prefer Y to X Or you are indifferent between X and Y

Asymmetrical Additionally, rational preferences have certain asymmetries. If X and Y are outcomes, then: You can’t both prefer X to Y and prefer Y to X. You can’t both prefer X to Y and be indifferent between X and Y.

Note We can combine connectedness and asymmetry and get: One and only one of the following is true for any two outcomes X and Y: You prefer X to Y. You prefer Y to X You are indifferent between X and Y.

Transitivity Rational preferences are also transitive, which means: If you think X is better than Y, and you think Y is better than Z, then you think X is better than Z too. If you think X is better than Y, and you think Y and Z are the same (you’re indifferent), then you think X is better than Z.
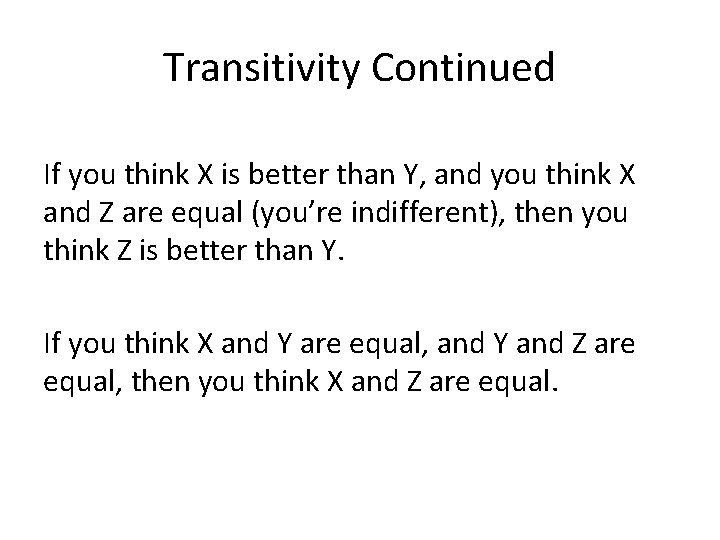
Transitivity Continued If you think X is better than Y, and you think X and Z are equal (you’re indifferent), then you think Z is better than Y. If you think X and Y are equal, and Y and Z are equal, then you think X and Z are equal.

Intransitivity Problems What’s wrong with intransitive preferences? Well suppose your preferences are intransitive in the following way: • You prefer A to B • You prefer B to C • You prefer C to A

The Money Pump Suppose I give you A. If you prefer C to A, you should be willing to give something up to trade A for C. Maybe it’s only something small, like $0. 10. If you prefer B to C, then you should give up $0. 10 again to trade C for B. If you prefer A to B, then you should give up $0. 10 again to trade B for A.

The Money Pump But now you started with A and paid $0. 30 to wind up with A again. If I keep trading you C for A, B for C, and then A for B, I can get as much money as I want out of you– millions, billions, or trillions of dollars. Obviously this would never happen– to anyone rational. That’s why we require that rational preferences be transitive.

Indifference Classes When your preferences are rational, in the sense of being connected, appropriately asymmetrical, and transitive, then we can divide all the possible outcomes into indifference classes.

Possible Rational Preferences You’re indifferent between A and B. You prefer A to C. You prefer C to D. You’re indifferent between D and E, E and F, and F and G. You prefer D to H. You’re indifferent between H and I. You prefer I to J.

Indifference Classes: Example Here, the indifference classes would be: 5. A, B 4. C 3. D, E, F, G 2. H, I 1. J

Indifference Classes In each case, you are indifferent to what is on any line (5, 4, 3, 2, 1) and you prefer what is on any higher numbered line to what is on any lower numbered line. The items on a given line are called the indifference classes and we can treat your preferences as preferences between indifference classes.

Numerical Representation The cool thing about rational preferences is that they allow you to divide people’s preferences into indifference classes. The cool thing about that is that it allows you to assign numbers to outcomes so that for any two outcomes X and Y, someone prefers X to Y = the number assigned to X is greater than the number assigned to Y; and she prefers Y to X = the number assigned to Y is greater than the number assigned to X.

Rational Preferences Needed For example, C is preferred to I, because 4 > 2. Notice that non-rational preferences can’t be assigned numbers like this. If you prefer X to Y and prefer Y to X, then there are no numbers n and m you can assign to X and Y such that: n>m>n

The numbers assigned to indifference classes are called utilities. (From the Latin word meaning ‘useful. ’) When people have rational preferences, we can replace their old decision tables containing outcomes with new decision tables containing utilities that represent those outcomes.

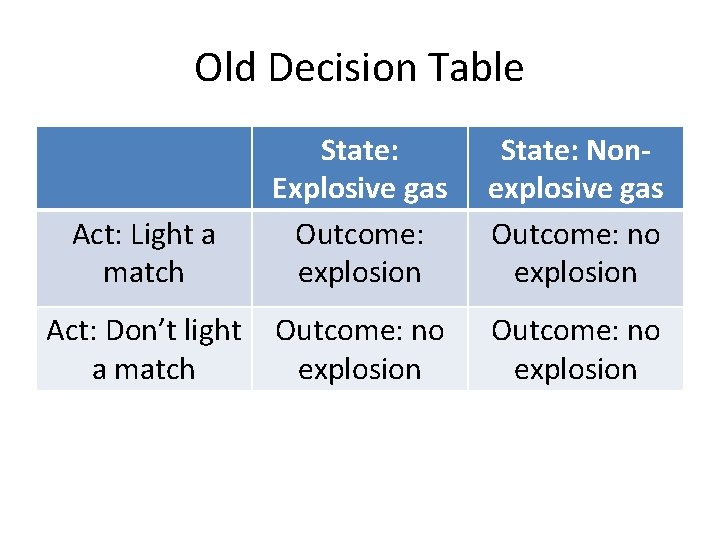
Old Decision Table Act: Light a match State: Explosive gas Outcome: explosion State: Nonexplosive gas Outcome: no explosion Act: Don’t light a match Outcome: no explosion

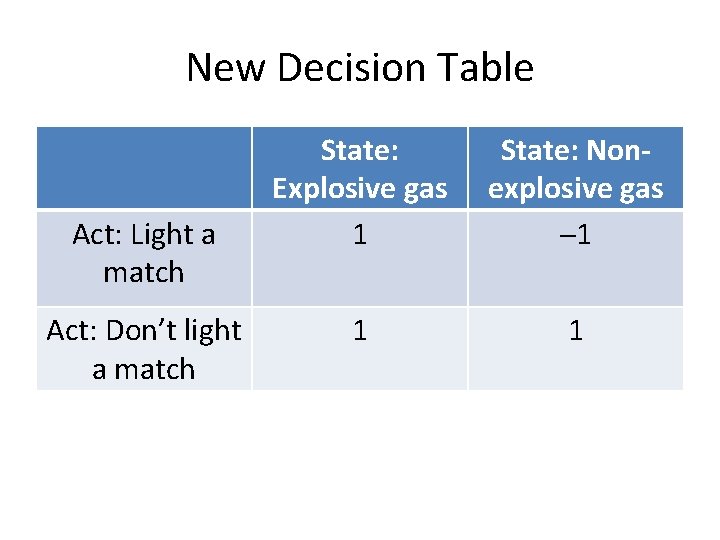
New Decision Table Act: Light a match Act: Don’t light a match State: Explosive gas 1 State: Nonexplosive gas ─1 1 1

Difference Our old decision table contained no information about what the person deciding preferred. This made it impossible to solve the decision problem: if they wanted an explosion more than anything, they should have lit the match. But who says that’s what they wanted, rather than something else? The new decision table contains the information about preferences.

Dollar Amounts When the outcomes are dollar amounts, we can often substitute dollars for utilities. Most people’s preferences for dollars are rational, for example, no one prefers $100 to $50, $50 to $25, and $25 to $100. No one both prefers $100 to $50 and also prefers $50 to $100. There are exceptions you can imagine, but they don’t occur often.

First Decision Rule: The Maximin Rule Next time we’ll look at various possible decision rules. Today I want to look at just one, the maximin rule. The maximin rule says to take the action whose minimum outcome is maximum (among all the other minimums). Here’s an example:

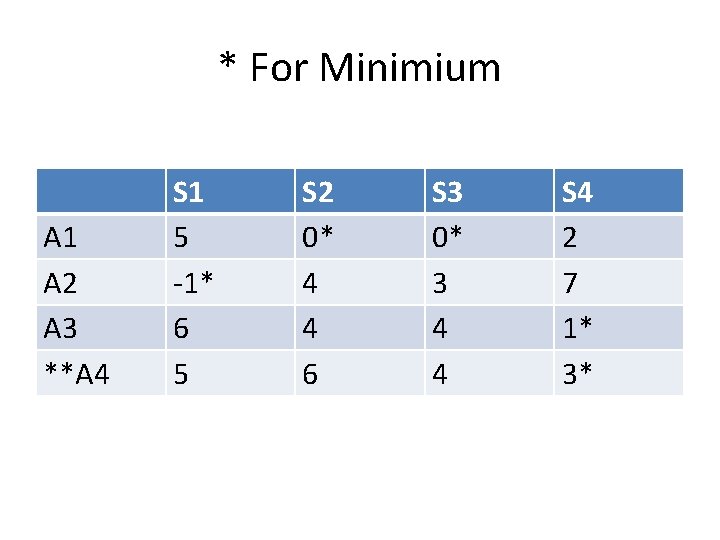
* For Minimium A 1 A 2 A 3 **A 4 S 1 5 -1* 6 5 S 2 0* 4 4 6 S 3 0* 3 4 4 S 4 2 7 1* 3*

The maximin rule recommends act A 4, because of all the minimum outcomes (min. A 1 = 0, min. A 2 = -1, min. A 3 = 1, and min. A 4 = 3), min. A 4 is the highest (maximum).

The maximin rule is a conservative decision rule. It says: look at all the possible outcomes for each of your acts. Find the worst possible scenario for each act (minimum). Pick the act that has the best (maximum) worst possible (minimum) scenario. Let’s consider how this applies to our decision table about the explosive gas.

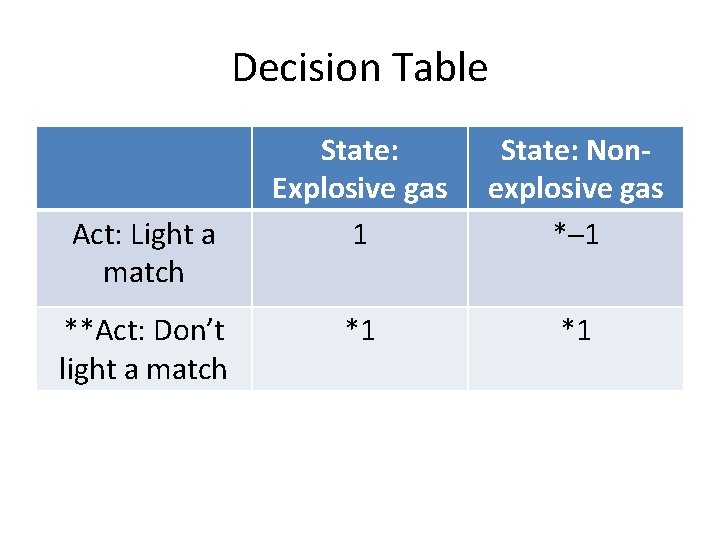
Decision Table Act: Light a match **Act: Don’t light a match State: Explosive gas 1 State: Nonexplosive gas *─1 *1 *1

Maximin Solution Here, the worst possible outcome of lighting a match is an explosion, min(Light Match) = -1. The worst possible outcome of not lighting a match is no explosion, min(Not Light) = 1. Since the agent prefers no explosion to an explosion (reflected in the fact that 1 > -1), we choose not lighting a match. The maximin rule tries to avoid catastrophe.

Is the maximin rule correct? We’ll talk about this next time when we talk about other rules, but notice that it has an odd consequence. Suppose you are faced with a decision under ignorance regarding a sports bet: you simply have no idea what the probabilities are that either team will win. This is the bet you are offered:

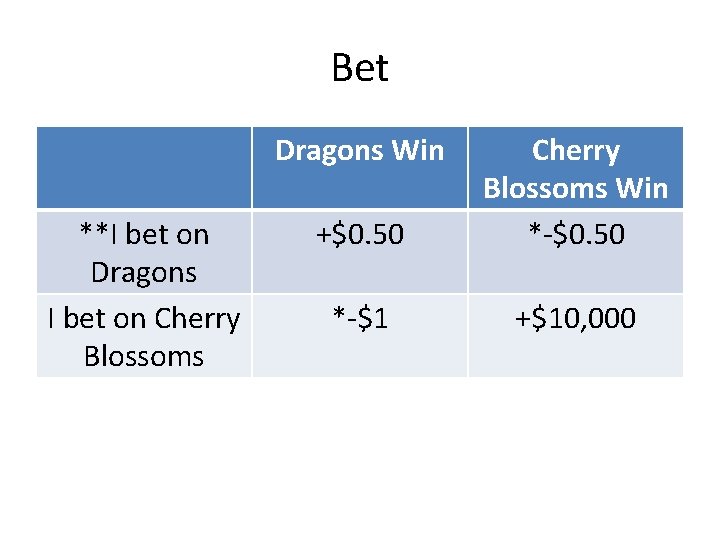
Bet Dragons Win **I bet on Dragons I bet on Cherry Blossoms +$0. 50 Cherry Blossoms Win *-$0. 50 *-$1 +$10, 000

Issues The maximin rule suggests that you bet on the Dragons, because the minimum payout is -$0. 50 which is higher than the minimum payout of -$1 for the Cherry Blossoms. But intuitively, this is too risk averse. You should obviously take the bet that could potentially net you $10, 000, at only a minor risk (-$1).

SUMMARY

Summary Decisions under ignorance involve choices where we cannot reasonably estimate the probabilities of the outcomes in different states. In order to aid in solving decision problems, we try to assign numerical values (utilities) to the different outcomes. In order for this to work, the person making the decision must have rational preferences: connected, asymmetric, and transitive.

Summary Sometimes dollar amounts can be used in place of utilities, when the outcomes are various dollar amounts, or things worth measurable dollar amounts. One rule for solving decision problems under ignorance is the maximin rule: to maximize the minimum outcome. The maximin rule is conservative, and maybe too conservative for a general rule.
 Good decision making poster
Good decision making poster Screening decisions and preference decisions
Screening decisions and preference decisions Plagiarism is deceitful because it is dishonest
Plagiarism is deceitful because it is dishonest Antecedent passion examples
Antecedent passion examples Consumer ignorance
Consumer ignorance Rawls social contract
Rawls social contract Veil of ignorance example
Veil of ignorance example Ignorance in fahrenheit 451
Ignorance in fahrenheit 451 Knowledge vs ignorance fahrenheit 451
Knowledge vs ignorance fahrenheit 451 The discovery of ignorance chapter 14
The discovery of ignorance chapter 14 Shit flows downstream
Shit flows downstream The crest of ignorance
The crest of ignorance Pluralitní ignorance
Pluralitní ignorance A christmas carol ignorance and want
A christmas carol ignorance and want Dwell in ignorance meaning
Dwell in ignorance meaning The crest of ignorance
The crest of ignorance Arguing with ignorance
Arguing with ignorance Contoh circulus in probando
Contoh circulus in probando What does appeal to ignorance mean
What does appeal to ignorance mean Deadlock ignorance in os
Deadlock ignorance in os Ignoranc
Ignoranc What do you guess the doctor gives coyotito?
What do you guess the doctor gives coyotito? Pluralistic ignorance
Pluralistic ignorance Social behavior psychology definition
Social behavior psychology definition Pluralistic ignorance
Pluralistic ignorance Plus j'apprends plus je me rends compte de mon ignorance
Plus j'apprends plus je me rends compte de mon ignorance Appeal to ignorance
Appeal to ignorance If you think training is expensive try ignorance
If you think training is expensive try ignorance Fallacy of equivocation
Fallacy of equivocation Dicto simpliciter example
Dicto simpliciter example Thoreau quotes self reliance
Thoreau quotes self reliance Area under velocity time graph
Area under velocity time graph Gradient of v-t graph
Gradient of v-t graph Ft=mv example
Ft=mv example Area under an acceleration time graph
Area under an acceleration time graph Momentum is
Momentum is Area under force time graph
Area under force time graph Time and value of supply under gst
Time and value of supply under gst Deceleration on velocity time graph
Deceleration on velocity time graph Start time end time and elapsed time
Start time end time and elapsed time International product decisions
International product decisions Bsg corporate lobby
Bsg corporate lobby Supply chain network design decisions
Supply chain network design decisions Product line pruning examples
Product line pruning examples Technical decisions in project charter
Technical decisions in project charter Product line decisions
Product line decisions Distribution logistics in marketing
Distribution logistics in marketing Political savvy pdf
Political savvy pdf Pharmasim presentation
Pharmasim presentation You make the decision - distribution decisions
You make the decision - distribution decisions Selective distribution channel
Selective distribution channel Average revenue
Average revenue Operational decisions: bump up your bumper
Operational decisions: bump up your bumper Framework for network design decisions
Framework for network design decisions Message decisions
Message decisions Media decisions in advertising
Media decisions in advertising Channel design decision
Channel design decision Factors influencing international pricing
Factors influencing international pricing Role of network design in supply chain
Role of network design in supply chain Evaluating selection techniques and decisions
Evaluating selection techniques and decisions Channel design decisions
Channel design decisions Describe the process specification structured decisions
Describe the process specification structured decisions Warehousing decisions
Warehousing decisions Pricing and output decisions in perfect competition
Pricing and output decisions in perfect competition An organized method for making good buying decisions.
An organized method for making good buying decisions.