Last Time Last time we looked at Gross

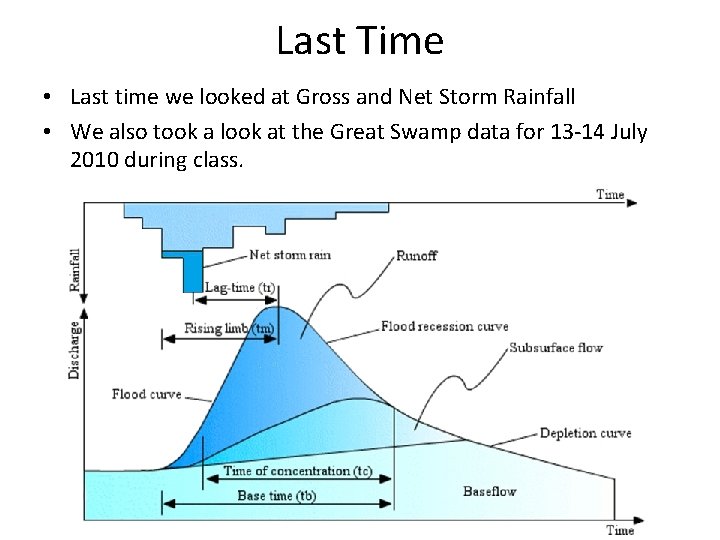
Last Time • Last time we looked at Gross and Net Storm Rainfall • We also took a look at the Great Swamp data for 13 -14 July 2010 during class.

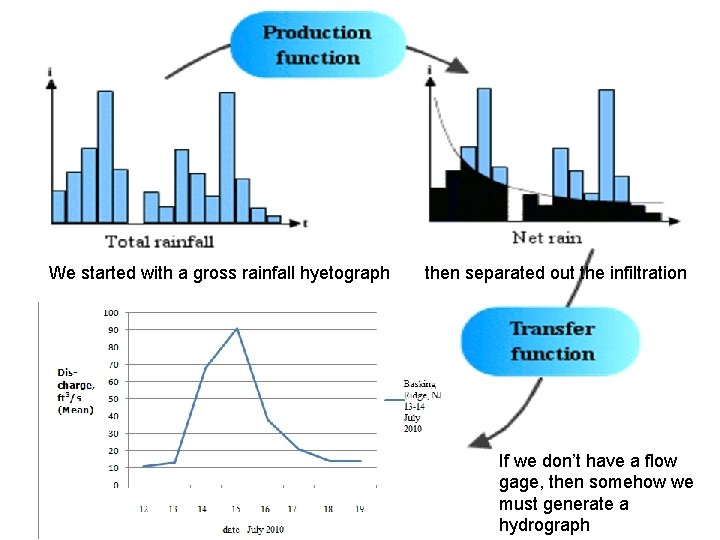
We started with a gross rainfall hyetograph then separated out the infiltration If we don’t have a flow gage, then somehow we must generate a hydrograph

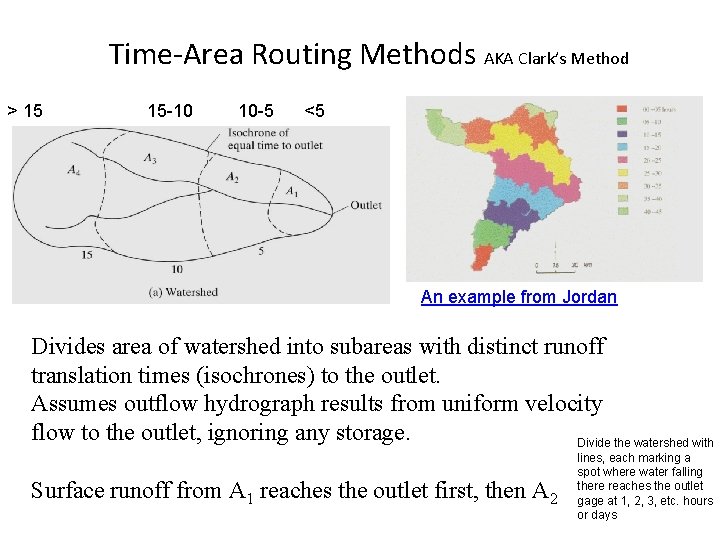
Time-Area Routing Methods AKA Clark’s Method > 15 15 -10 10 -5 <5 An example from Jordan Divides area of watershed into subareas with distinct runoff translation times (isochrones) to the outlet. Assumes outflow hydrograph results from uniform velocity flow to the outlet, ignoring any storage. Divide the watershed with Surface runoff from A 1 reaches the outlet first, then A 2 lines, each marking a spot where water falling there reaches the outlet gage at 1, 2, 3, etc. hours or days

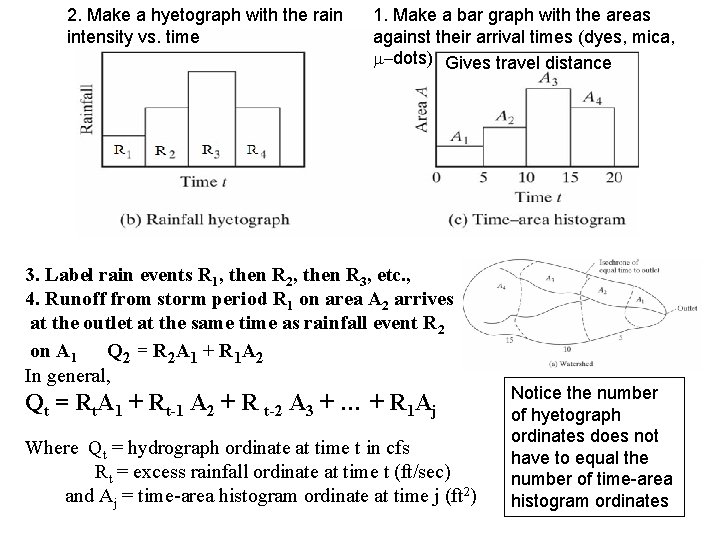
2. Make a hyetograph with the rain intensity vs. time 1. Make a bar graph with the areas against their arrival times (dyes, mica, m-dots) Gives travel distance 3. Label rain events R 1, then R 2, then R 3, etc. , 4. Runoff from storm period R 1 on area A 2 arrives at the outlet at the same time as rainfall event R 2 on A 1 Q 2 = R 2 A 1 + R 1 A 2 In general, Qt = Rt. A 1 + Rt-1 A 2 + R t-2 A 3 + … + R 1 Aj Where Qt = hydrograph ordinate at time t in cfs Rt = excess rainfall ordinate at time t (ft/sec) and Aj = time-area histogram ordinate at time j (ft 2) Notice the number of hyetograph ordinates does not have to equal the number of time-area histogram ordinates

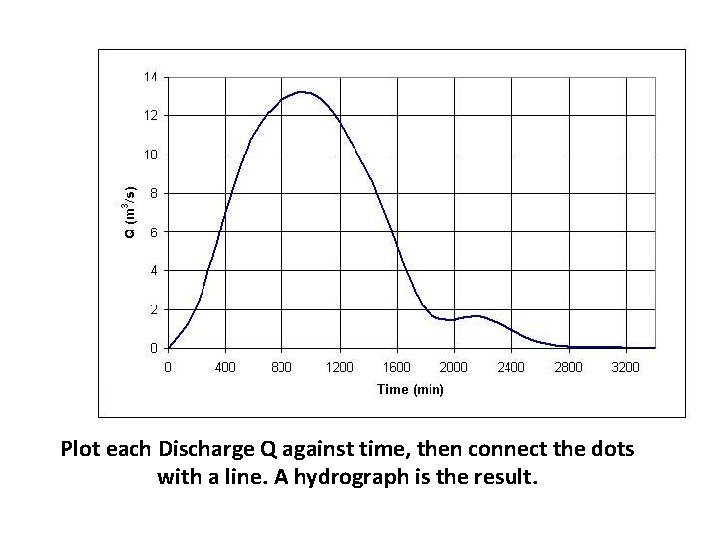
Plot each Discharge Q against time, then connect the dots with a line. A hydrograph is the result.

An Example • As usual, I’ll go through an example in the text, then you will do a similar problem. This method being used for studies around the Great Lakes

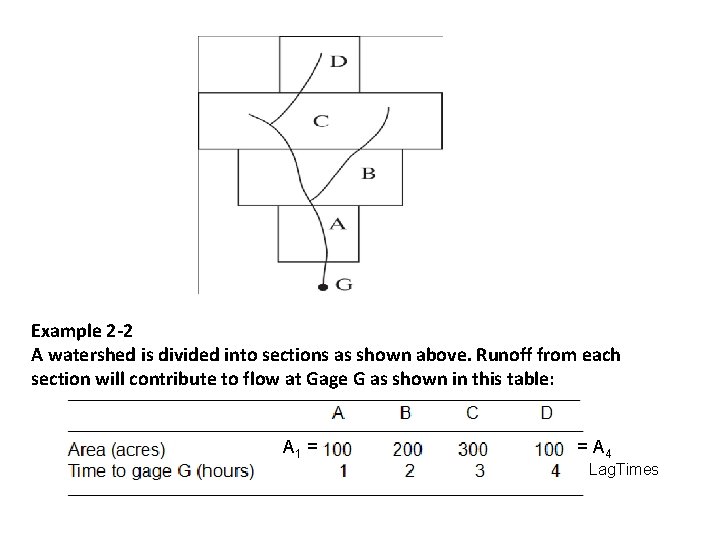
Example 2 -2 A watershed is divided into sections as shown above. Runoff from each section will contribute to flow at Gage G as shown in this table: __________________________ A B C D _______________________________________ Area (acres) Time to gage G (hours) A 1 = 100 1 200 2 300 3 100 = A 4 4 Lag. Times _______________________________________

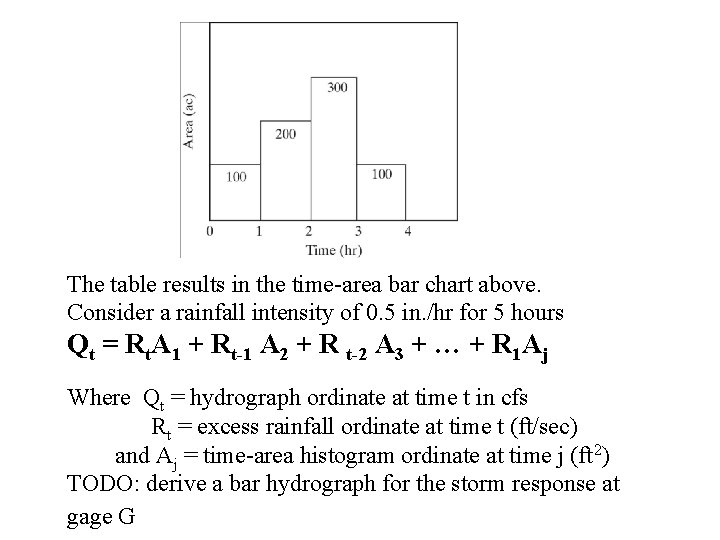
The table results in the time-area bar chart above. Consider a rainfall intensity of 0. 5 in. /hr for 5 hours Qt = Rt. A 1 + Rt-1 A 2 + R t-2 A 3 + … + R 1 Aj Where Qt = hydrograph ordinate at time t in cfs Rt = excess rainfall ordinate at time t (ft/sec) and Aj = time-area histogram ordinate at time j (ft 2) TODO: derive a bar hydrograph for the storm response at gage G

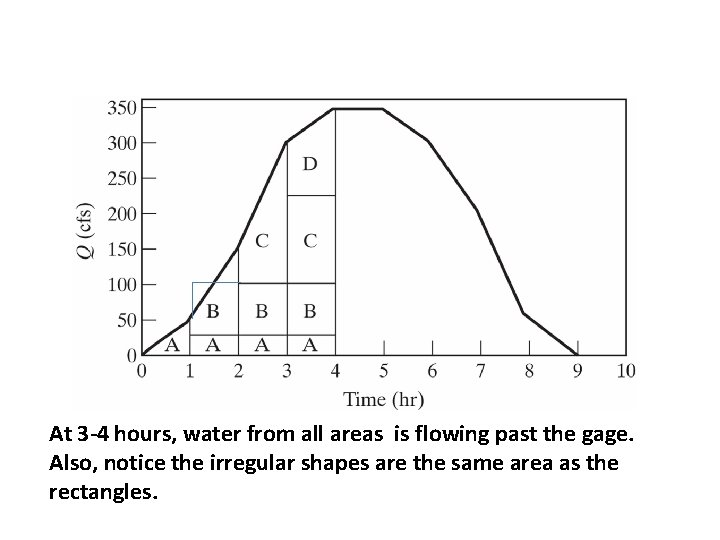
At 3 -4 hours, water from all areas is flowing past the gage. Also, notice the irregular shapes are the same area as the rectangles.

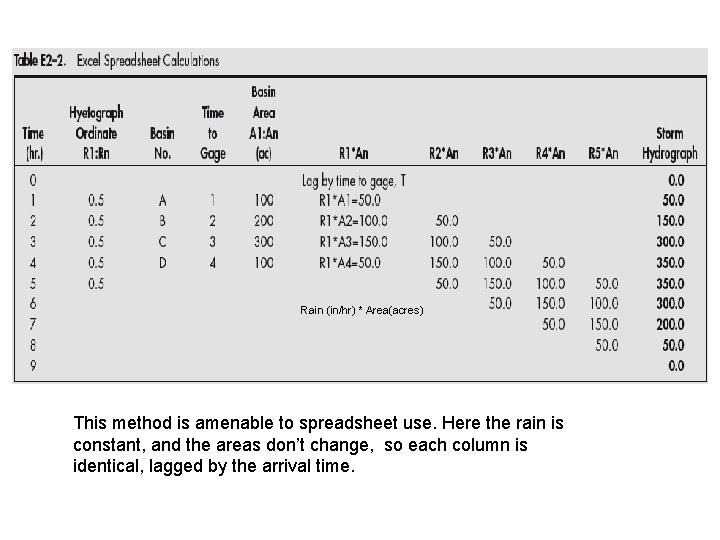
Rain (in/hr) * Area(acres) This method is amenable to spreadsheet use. Here the rain is constant, and the areas don’t change, so each column is identical, lagged by the arrival time.

Rain (in/hr) * Area(acres) = Vol/time • Rain (in/hr) * Area(acres) x 43, 560 ft 2/ 1 acre • x 1 foot/12 inches x 1 hour/3600 sec • so • 1 inch. acre/hour = 1. 008333 ft 3/sec ~ 1 cfs