Greedy Algorithms make decisions greedily previous decisions are












![Dynamic Programming – Activity selection 2 S[k, j ] = max j’: f[j’] · Dynamic Programming – Activity selection 2 S[k, j ] = max j’: f[j’] ·](https://slidetodoc.com/presentation_image/d266b515d78c3dfec93c1b680ab569b6/image-26.jpg)













![Problem: Huffman Coding - optimal prefix-free code Huffman ( [a 1, f 1], [a Problem: Huffman Coding - optimal prefix-free code Huffman ( [a 1, f 1], [a](https://slidetodoc.com/presentation_image/d266b515d78c3dfec93c1b680ab569b6/image-40.jpg)




- Slides: 44

Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems Input: Output: Objective:

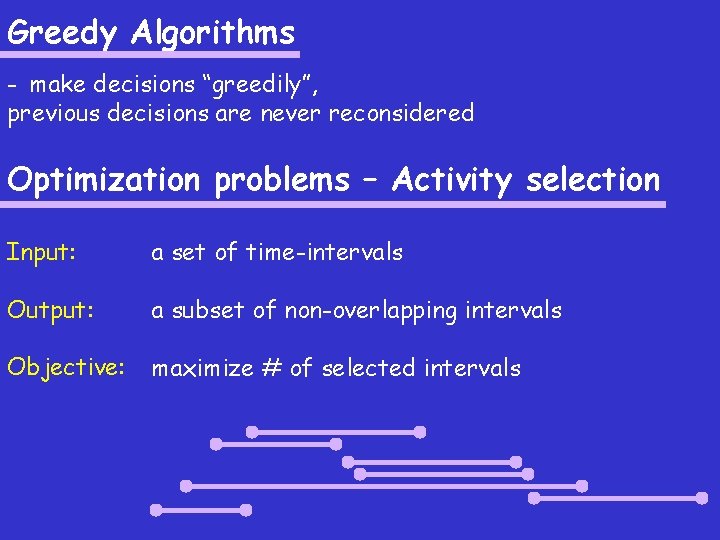
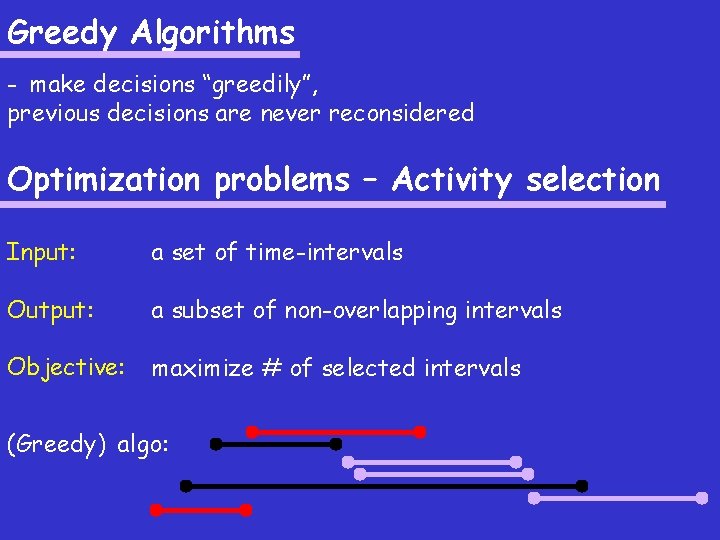
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals

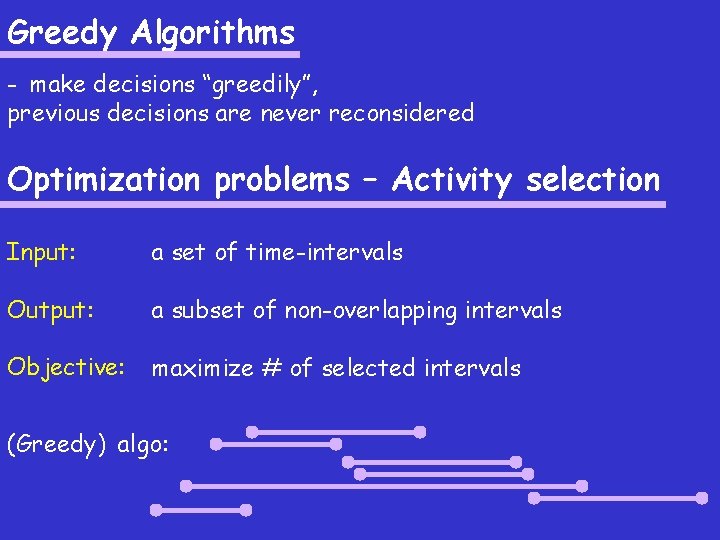
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals (Greedy) algo:

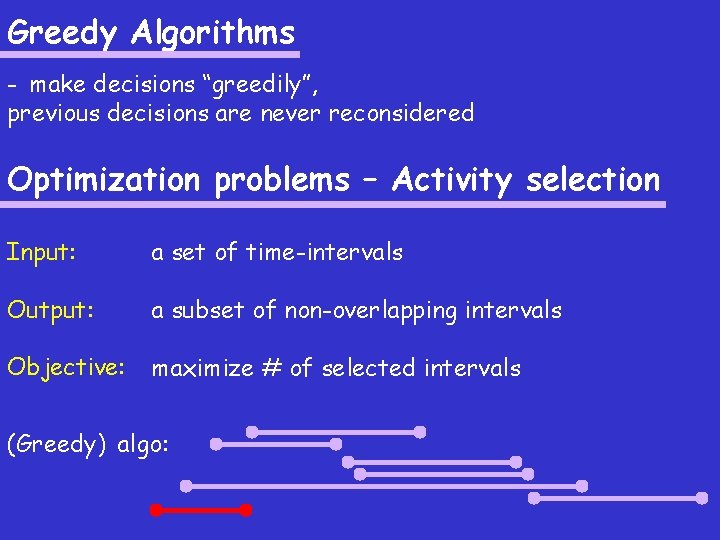
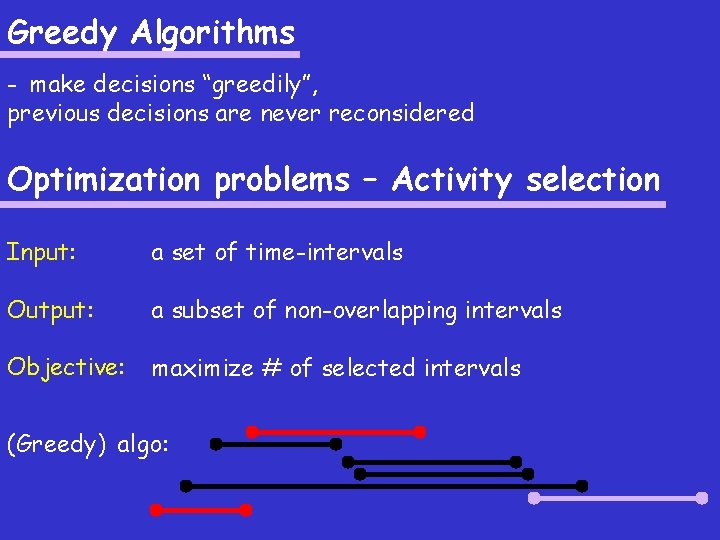
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals (Greedy) algo:

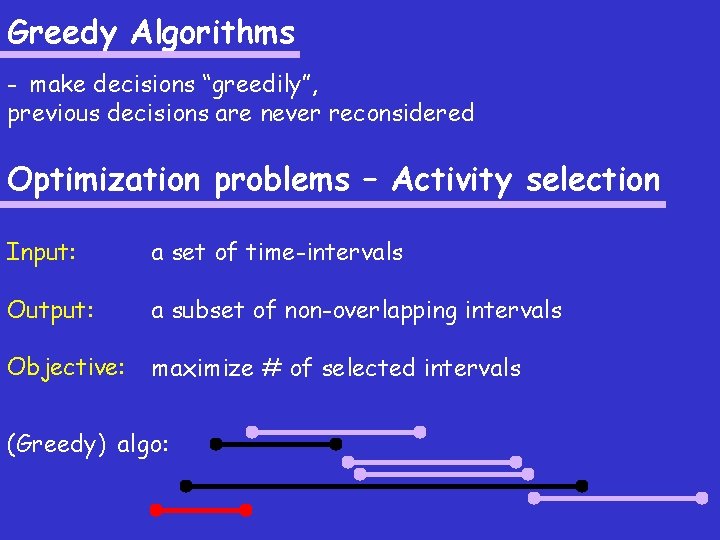
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals (Greedy) algo:

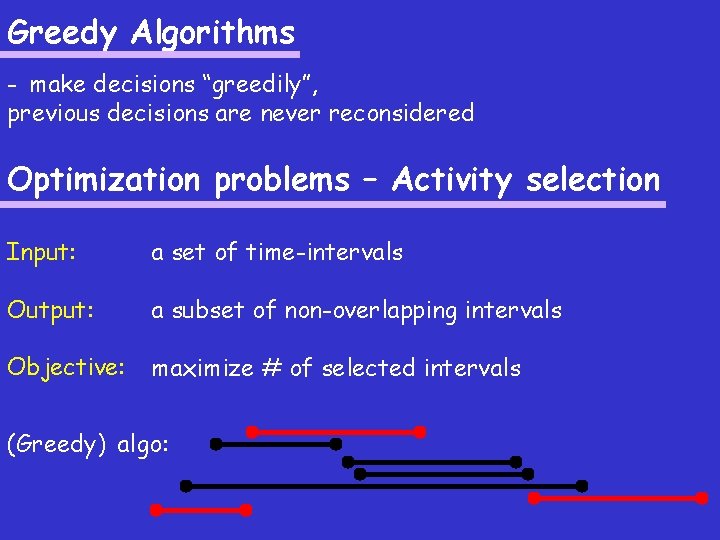
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals (Greedy) algo:

Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals (Greedy) algo:

Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals (Greedy) algo:

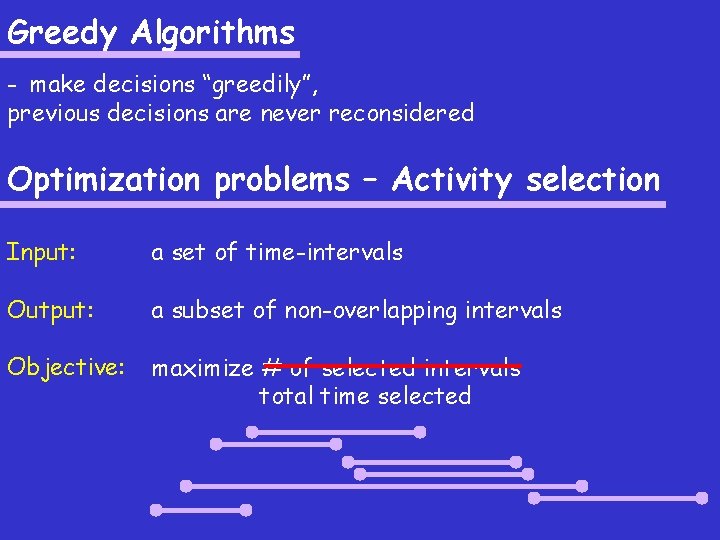
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals total time selected

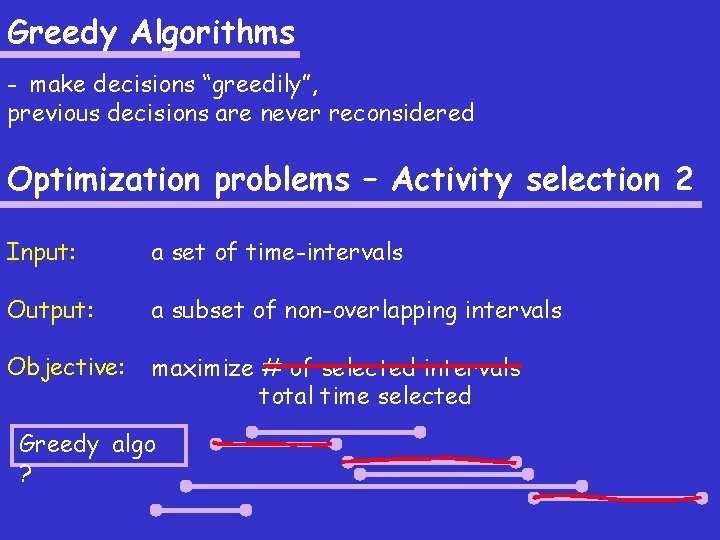
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection 2 Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals total time selected Greedy algo ?

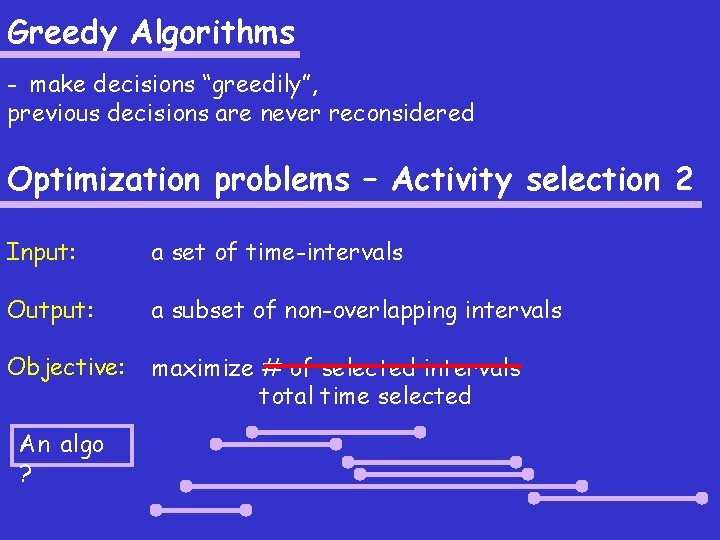
Greedy Algorithms - make decisions “greedily”, previous decisions are never reconsidered Optimization problems – Activity selection 2 Input: a set of time-intervals Output: a subset of non-overlapping intervals Objective: maximize # of selected intervals total time selected An algo ?

Back. Tracking - “brute force”: try all possibilities - running time?

Back. Tracking - “brute force”: try all possibilities - running time? O(n!) Anything better for Activity selection 2?

Back. Tracking - “brute force”: try all possibilities - running time? O(n!) Anything better for Activity selection 2?

Back. Tracking - “brute force”: try all possibilities - running time? O(n!) Anything better for Activity selection 2? - dynamic programming

Dynamic Programming - idea: remember values for smaller instances, use it for computing the value for a larger instance

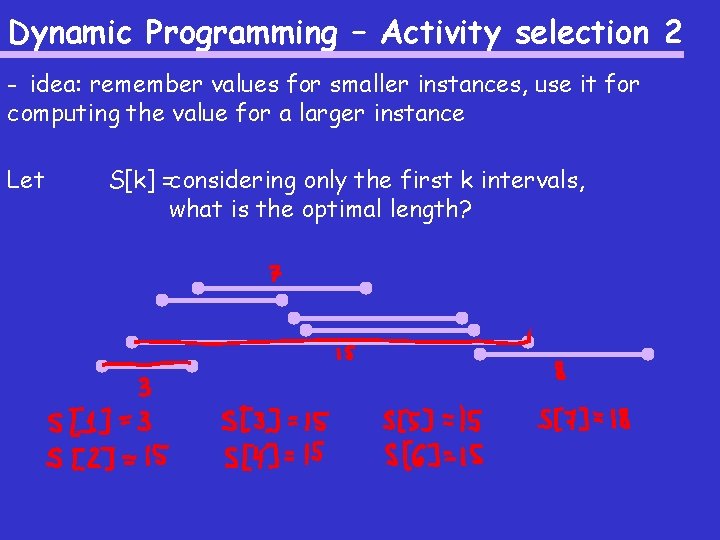
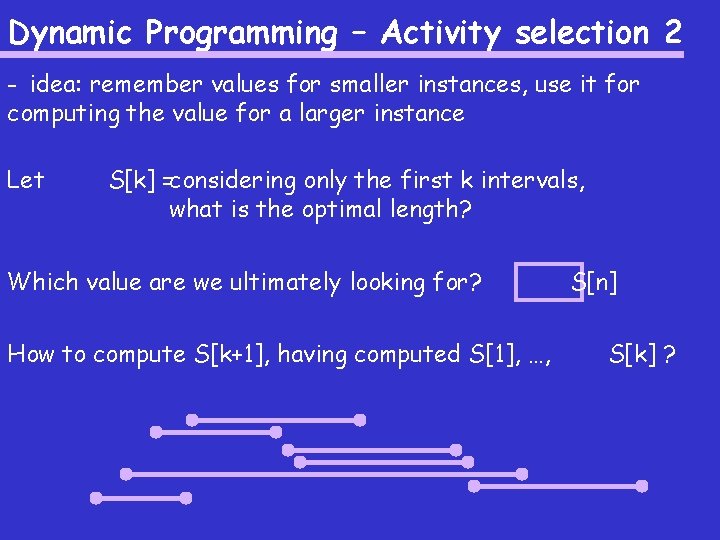
Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k] =considering only the first k intervals, what is the optimal length?

Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k] =considering only the first k intervals, what is the optimal length? Which value are we ultimately looking for?

Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k] =considering only the first k intervals, what is the optimal length? Which value are we ultimately looking for? How to compute S[k+1], having computed S[1], …, S[n] S[k] ?

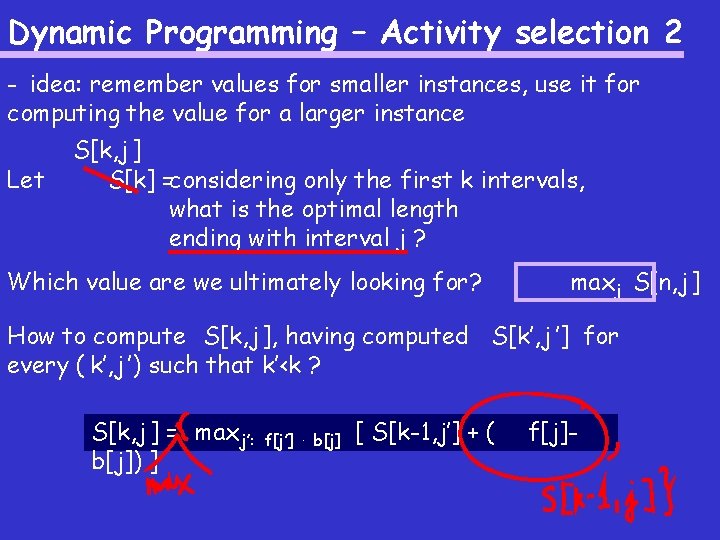
Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k, j ] S[k] =considering only the first k intervals, what is the optimal length ending with interval j ? Which value are we ultimately looking for? How to compute S[k+1], having computed S[1], …, S[n] S[k] ?

Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k, j ] S[k] =considering only the first k intervals, what is the optimal length ending with interval j ? Which value are we ultimately looking for? How to compute S[k+1], having computed S[1], …, S[n] S[k] ?

Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k, j ] S[k] =considering only the first k intervals, what is the optimal length ending with interval j ? Which value are we ultimately looking for? How to compute S[k+1], having computed S[1], …, max j S[n, j ] S[k] ?

Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k, j ] S[k] =considering only the first k intervals, what is the optimal length ending with interval j ? Which value are we ultimately looking for? How to compute S[k+1], having computed S[1], …, max j S[n, j ] S[k] ? ?

Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k, j ] S[k] =considering only the first k intervals, what is the optimal length ending with interval j ? Which value are we ultimately looking for? max j S[n, j ] How to compute S[k, j ], having computed S[k’, j ’] for every ( k’, j ’) such that k’<k ?

Dynamic Programming – Activity selection 2 - idea: remember values for smaller instances, use it for computing the value for a larger instance Let S[k, j ] S[k] =considering only the first k intervals, what is the optimal length ending with interval j ? Which value are we ultimately looking for? max j S[n, j ] How to compute S[k, j ], having computed S[k’, j ’] for every ( k’, j ’) such that k’<k ? S[k, j ] = max j’: b[j]) ] f[j’] · b[j] [ S[k-1, j’] + ( f[j]-
![Dynamic Programming Activity selection 2 Sk j max j fj Dynamic Programming – Activity selection 2 S[k, j ] = max j’: f[j’] ·](https://slidetodoc.com/presentation_image/d266b515d78c3dfec93c1b680ab569b6/image-26.jpg)
Dynamic Programming – Activity selection 2 S[k, j ] = max j’: f[j’] · b[j] [ S[k-1, j’] + ( f[j]b[j]) ] Can output the optimal time, how to find the optimal selection?

Approaches to Problem Solving • greedy algorithms • dynamic programming • backtracking • divide-and-conquer

Approaches to Problem Solving • greedy algorithms • dynamic programming • backtracking • divide-and-conquer our focus this week

Problem: Huffman Coding binary character code = assignment of binary strings to characters e. g. ASCII code A = 01000001 B = 01000010 C = 01000011 … How to decode: fixed-length code ? 01000001010000100100001101000001

Problem: Huffman Coding binary character code = assignment of binary strings to characters e. g. code A = 0 B = 10 C = 11 … How to decode: variable-length code ? 0101001111

Problem: Huffman Coding binary character code = assignment of binary strings to characters e. g. code A = 0 B = 10 C = 11 … How to decode: variable-length code DEF: ? 0101001111 A code is prefix-free if no codeword is a prefix of another codeword.

Problem: Huffman Coding binary character code = assignment of binary strings to characters e. g. another code A = 1 B = 10 C = 11 … How to decode: 10101111 variable-length code DEF: ? A code is prefix-free if no codeword is a prefix of another codeword.

Problem: Huffman Coding binary character code = assignment of binary strings to characters e. g. another code not prefix. A = 1 free B = 10 C = 11 … How to decode: 10101111 ? variable-length code DEF: A code is prefix-free if no codeword is a prefix of another codeword.

Problem: Huffman Coding - optimal prefix-free code E 11. 1607% M 3. 0129% A 8. 4966% H 3. 0034% R 7. 5809% G 2. 4705% I 7. 5448% B 2. 0720% O 7. 1635% F 1. 8121% T 6. 9509% Y 1. 7779% N 6. 6544% W 1. 2899% S 5. 7351% K 1. 1016% L 5. 4893% V 1. 0074% C 4. 5388% X 0. 2902% U 3. 6308% Z 0. 2722% D 3. 3844% J 0. 1965% P 3. 1671% Q 0. 1962% Input: an alphabet with frequencies Output: prefix code Objective: expected number of bits per character

Problem: Huffman Coding - optimal prefix-free code A B C D Input: an alphabet with frequencies Output: prefix code Objective: expected number of bits per character 60% 20% 10%

Problem: Huffman Coding - optimal prefix-free code 00 01 10 11 A B C D Input: an alphabet with frequencies Output: prefix code Objective: expected number of bits per character 60% 20% 10%

Problem: Huffman Coding - optimal prefix-free code Optimal ? 00 01 10 11 A B C D Input: an alphabet with frequencies Output: prefix code Objective: expected number of bits per character 60% 20% 10%

Problem: Huffman Coding - optimal prefix-free code Optimal ? 2 -bits per character Can do better ? 00 01 10 11 A B C D Input: an alphabet with frequencies Output: prefix code Objective: expected number of bits per character 60% 20% 10%

Problem: Huffman Coding - optimal prefix-free code Optimal ? 2 -bits per character Can do better ? 00 01 10 11 A B C D YES, 1. 6 -bits per character Input: an alphabet with frequencies Output: prefix code Objective: expected number of bits per character 60% 20% 10%
![Problem Huffman Coding optimal prefixfree code Huffman a 1 f 1 a Problem: Huffman Coding - optimal prefix-free code Huffman ( [a 1, f 1], [a](https://slidetodoc.com/presentation_image/d266b515d78c3dfec93c1b680ab569b6/image-40.jpg)
Problem: Huffman Coding - optimal prefix-free code Huffman ( [a 1, f 1], [a , f 2], …, [an, fn]) 2 if n=1 then code[a 1] “” else let fi, fj be the 2 smallest f’s Huffman ( [ai, fi+fj], [a 1, f 1], …, [an, fn] ) code[aj] code[ai] + “ 0” code[ai] + “ 1”

Problem: Huffman Coding Lemma 1: Let x, y be the symbols with frequencies fx < fy. Then in an optimal prefix code length(C x) length(C y).

Problem: Huffman Coding Lemma 1: Let x, y be the symbols with frequencies fx < fy. Then in an optimal prefix code length(C x) length(C y). Lemma 2: Let C = w 0 be a longest codeword in an optimal code. Then w 1 is also a codeword.

Problem: Huffman Coding Lemma 1: Let x, y be the symbols with frequencies fx < fy. Then in an optimal prefix code length(C x) length(C y). Lemma 2: Let C = w 0 be a longest codeword in an optimal code. Then w 1 is also a codeword. Lemma 3: Let x, y be the symbols with the smallest frequencies. Then there exists an optimal prefix code such that the codewords for x and y differ only in the last bit.

Problem: Huffman Coding Lemma 1: Let x, y be the symbols with frequencies fx < fy. Then in an optimal prefix code length(C x) length(C y). Lemma 2: Let C = w 0 be a longest codeword in an optimal code. Then w 1 is also a codeword. Lemma 3: Let x, y be the symbols with the smallest frequencies. Then there exists an optimal prefix code such that the codewords for x and y differ only in the last bit. Theorem: The prefix code output by the Huffman algorithm is optimal.