Datenanalyse und deskriptive Statistik Einleitung Explorative Datenanalyse Kennwerte

Datenanalyse und deskriptive Statistik • • Einleitung Explorative Datenanalyse Kennwerte statistischer Verteilungen Statistik in der Messtechnik Ausgleichungsrechnung I Gerhard Navratil

Einleitung Statistik: Zweig der angewandten Mathematik zerfällt in – Deskriptive Statistik: Beschreibt Datenmengen – Induktive Statistik: Schließt von kleinem Ausschnitt auf das Ganze (siehe Kapitel 8 ) Ziel: Verständnis der statistischen Konzepte Vorgangsweise: Empirische Betrachtung anhand geodätischer Messungen Ausgleichungsrechnung I Gerhard Navratil

Aufgaben der deskriptiven Statistik Wir beschreiben die ‚Wirklichkeit‘ oft mit Zahlen, z. B. – Jahresbilanz eines Unternehmens – Verhältnis Waldflächen – Gesamtfläche eines Landes –… Mit deskriptiver Statistik stellen wir die Zahlen zusammen Aussagen über Struktur und Gesetzmäßigkeiten Ausgleichungsrechnung I Gerhard Navratil

Beispiel 1 Distanz mehrfach mit einem Maßband d gemessen [m] Was können wir herauslesen? 5, 2 1 4 Häufigkeit der Einzelwerte 5, 2 2 8 Minimum/Maximum 5, 2 3 2 Lücke? 5, 2 Bessere Ergebnisse bei mehr Messungen? 4 3 5, 2 5 4 Ausgleichungsrechnung I Gerhard Navratil

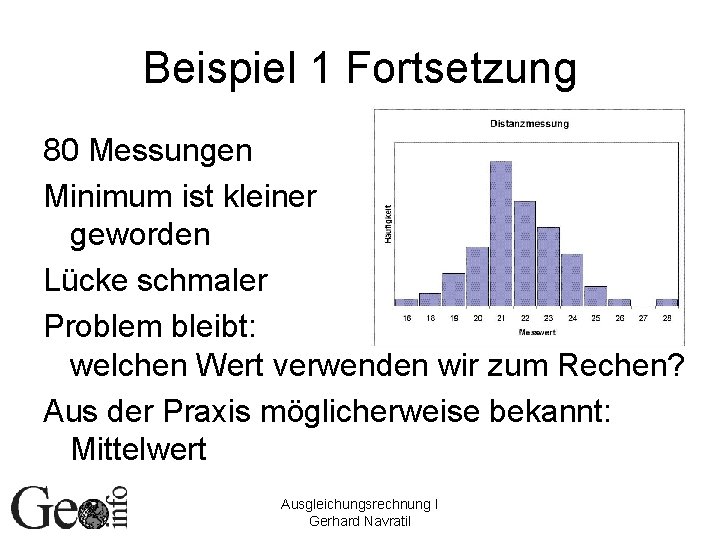
Beispiel 1 Fortsetzung 80 Messungen Minimum ist kleiner geworden Lücke schmaler Problem bleibt: welchen Wert verwenden wir zum Rechen? Aus der Praxis möglicherweise bekannt: Mittelwert Ausgleichungsrechnung I Gerhard Navratil

Beispiel 2 Strecke mit 3 Geräten gemessen Charakterisierender Wert? Mittelwert 574, 751 m Ausreißer? Messreihe x DI 1600 3 mm+2 ppm Messreihe y DI 2002 1 mm+1 ppm Messreihe z ME 5000 0, 2 mm+0, 2 ppm 574, 775 574, 772 574, 775 574, 777 574, 775 574, 773 574, 777 574, 776 574, 770 574, 173 574, 775 574, 774 574, 775 574, 772 574, 773 574, 774 574, 776 574, 773 574, 779 574, 774 Ausgleichungsrechnung I Gerhard Navratil

Skalenniveaus • • • Nominalskala: Identität kategorisch Ordinalskala: Ordnungsrelation Intervallskala: Differenzen metrisch Rationalskala: Quotienten Absolutskala: natürliche Maßeinheit repräsentieren physikalische Größen Ausgleichungsrechnung I Gerhard Navratil

Nominalskala Werte dienen nur zur Benennung z. B. Beruf, Geschlecht, Blutgruppe Erfüllt sind folgende Bedingungen – Reflexivität: a = a – Symmetrie: a = b b = a – Transitivität: a = b b = c a = c Sortieren nicht erlaubt! Ausgleichungsrechnung I Gerhard Navratil

Ordinalskala Reihung der Werte z. B. Resultat eines Wettbewerbs, militärischer Rang, akademischer Grad Keine Aussage über die Abstände der Klassen Erfüllt sind folgende Bedingungen – Konnexivität: es gilt immer a > b oder a < b oder a = b – Transitivität: a > b b > c a > c Spezialfall: Rangskala – jeder Wert genau einmal vertreten Ausgleichungsrechnung I Gerhard Navratil

Intervallskala Differenzen von Werten sind vergleichbar Aber: Kein absoluter Nullpunkt, Verhältnisse sind also nicht sinnvoll z. B. Temperatur in Grad Celsius, geogr. Länge Zusätzliche Operationen: Addition, Subtraktion Mittelbildung möglich Ausgleichungsrechnung I Gerhard Navratil

Verhältnis-/Rationalskala Besitzt absoluten Nullpunkt z. B. Temperatur in Kelvin, Distanz zwischen zwei Punkten Multiplikation und Division möglich Ausgleichungsrechnung I Gerhard Navratil

Absolutskala Entspricht einer Rationalskala, aber: Es gibt eine natürliche Maßeinheit meist: Stück (im weitesten Sinne) z. B. Anzahl der Teilnehmer Ausgleichungsrechnung I Gerhard Navratil

Skalenniveaus in Vermessung und Geoinformation Vermessung: i. A. metrische Daten (also Intervall- oder Rationalskala) GIS: Metrische Daten möglich (z. B. Straßenbreite, Lichtintensität einzelner Bildpunkte) Oft aber auch kategorische Daten (Bodenbedeckung, Eigentümer, …) Ausgleichungsrechnung I Gerhard Navratil

Methoden der explorativen Datenanalyse Ausgangspunkt: Ungefähre Vorstellung, wie unsere Datenmenge aussehen sollte (stochastisches Modell) Daten, die nicht ins Modell passen, sollen eliminiert werden: Ausreißer Im Beispiel 2: Messwert 574, 173 m (Messfehler, Schreibfehler? ? ? ) Nachträgliches Ändern von Daten problematisch Eliminieren Ausgleichungsrechnung I Gerhard Navratil

Erster Schritt Überblick verschaffen Urliste muss also anschaulich dargestellt werden 2 Möglichkeiten – Tabellarische Darstellung – Grafische Darstellung Ausgleichungsrechnung I Gerhard Navratil

Tabellarische Darstellung Einteilung der Daten in Klassen Zu jeder Klasse werden Häufigkeiten angegeben (wie viele Werte sind in der Klasse) Ausgleichungsrechnung I Gerhard Navratil

Klassenbildung Aufteilung des Wertebereiches in Teilbereiche (Klassen) – Vollständige Überdeckung des Wertebereiches Wenige Klassen: Übersichtlich aber großer Informationsverlust Faustformeln: Ausgleichungsrechnung I Gerhard Navratil

Klassengrenzen Klassenbreite: Bei offenen Klassen liegen die xmin und xmax in den offenen Klassen (erste und letzte Klasse) Arithmetischer Mittelwert der Klassengrenzen: Klassenmitte Oft nur mehr Klassenmitte und Häufigkeit gegeben Werte auf Klassengrenze fallen halb in jede Klasse Ausgleichungsrechnung I Gerhard Navratil

Häufigkeitstabellen (1) Anzahl der Elemente pro Klasse Unterscheidung – absolut – relativ – Häufigkeitssumme Absolute Häufigkeit ki – Probe Absolute Häufigkeitssumme: Anzahl der Werte, die einen bestimmten Wert nicht übersteigen Ausgleichungsrechnung I Gerhard Navratil

Häufigkeitstabellen (2) Relative Häufigkeiten hi – Probe Relative Häufigkeitssumme: Absolute Häufigkeitssumme dividiert durch Gesamtzahl der Beobachtungen Ausgleichungsrechnung I Gerhard Navratil

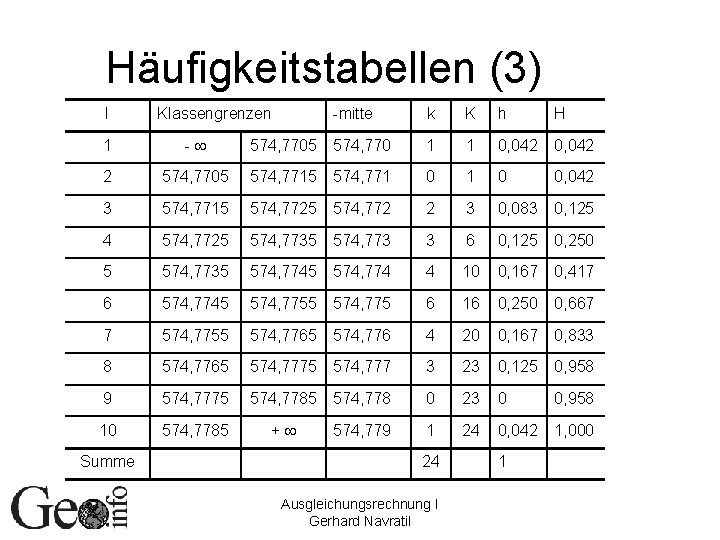
Häufigkeitstabellen (3) I Klassengrenzen -mitte k K h H 1 - 574, 7705 574, 770 1 1 0, 042 2 574, 7705 574, 771 0 1 0 0, 042 3 574, 7715 574, 772 2 3 0, 083 0, 125 4 574, 7725 574, 773 3 6 0, 125 0, 250 5 574, 7735 574, 774 4 10 0, 167 0, 417 6 574, 7745 574, 775 6 16 0, 250 0, 667 7 574, 7755 574, 776 4 20 0, 167 0, 833 8 574, 7765 574, 777 3 23 0, 125 0, 958 9 574, 7775 574, 778 0 23 0 0, 958 10 574, 7785 + 574, 779 1 24 0, 042 1, 000 Summe 24 Ausgleichungsrechnung I Gerhard Navratil 1

Darstellung als Funktion (empirische) Verteilungsfunktion Ordnet jedem Beobachtungswert die absolute (relative) Häufigkeit(ssumme) zu z. B. Die Sprungstellen lassen sich vermeiden Ausgleichungsrechnung I Gerhard Navratil

Graphische Darstellungen • Histogramm • Kurvendarstellung • Stamm-und-Blatt-Plan Ausgleichungsrechnung I Gerhard Navratil

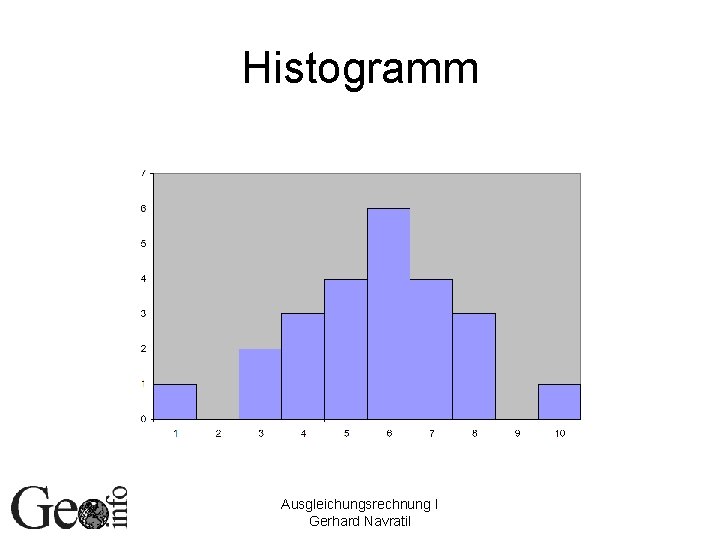
Histogramm Ausgleichungsrechnung I Gerhard Navratil

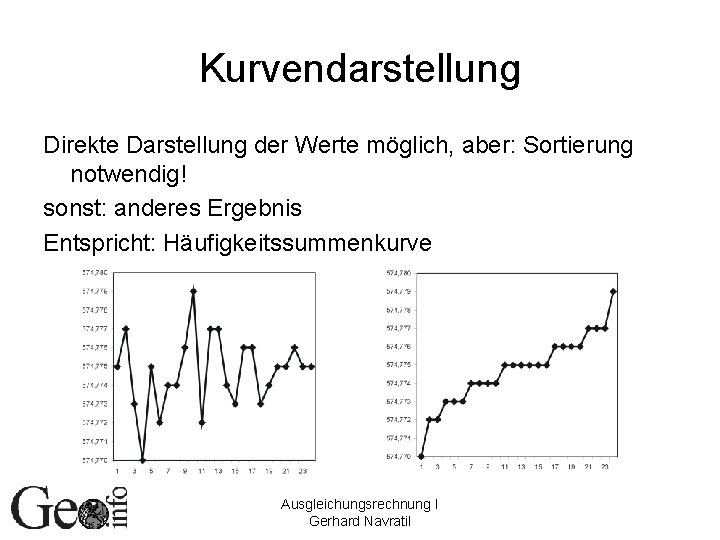
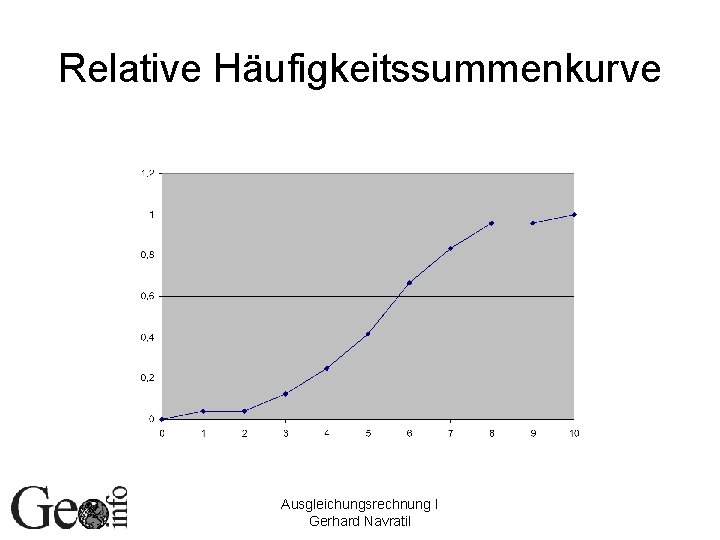
Kurvendarstellung Direkte Darstellung der Werte möglich, aber: Sortierung notwendig! sonst: anderes Ergebnis Entspricht: Häufigkeitssummenkurve Ausgleichungsrechnung I Gerhard Navratil

Relative Häufigkeitssummenkurve Ausgleichungsrechnung I Gerhard Navratil

Stamm-und-Blatt-Plan K [cm] 1 57477 0 1 K [cm] 57477 0 3 22 1 6 333 6 10 4444 16 4444555555 16 555555 23 6666777 20 6666 24 9 23 777 23 24 9 Ausgleichungsrechnung I Gerhard Navratil 22333

Kennwerte empirischer Häufigkeitsverteilungen (1) Häufigkeitsverteilung: Zusammenhang zwischen Beobachtungswerten und Häufigkeiten • Einzelnes Merkmal: univariate Verteilung • Zwei Merkmale: bivariate Verteilung • Sonst: multivariate Verteilung Ausgleichungsrechnung I Gerhard Navratil

Kennwerte empirischer Häufigkeitsverteilungen (2) Kenngrößen charakterisieren – Lage – Streuung – Form Jeder Messwert hat Rangzahl (Ordnungsnummer in der Folge der Beobachtungen) Üblicherweise berechnet aus großen Beobachtungsreihen (n=10 absolutes Minimum, oft n>100) Ausgleichungsrechnung I Gerhard Navratil

Lagekennwerte (1) • • Minimaler/maximaler Wert Arithmetisches Mittel Geometrisches Mittel Quantile: Zerlegt die Datenmenge in zwei Bereiche – a-Quantil trennt a% der Daten ab (z. B. 0, 1 -Quantil oder 10%-Quantil) • Median: 0, 5 -Quantil – auch: Perzentil Ausgleichungsrechnung I Gerhard Navratil

Lagekennwerte (2) • Quartile: 0, 25 - und 0, 75 -Quantil • Modalwert: Am häufigsten vorkommender Wert Ausgleichungsrechnung I Gerhard Navratil

Streuungskennwerte • Spannweiten – Spannweite – Quartilsspannweite • Empirische Varianz: D=xmax-xmin D 0, 25=x 3/4 -x 1/4 • Empirische Standardabweichung: • Empirischer Variationskoeffizient: Ausgleichungsrechnung I Gerhard Navratil

Zentrieren und Standardisieren • Zentrierter Beobachtungswert • Standardisierter Beobachtungswert Ausgleichungsrechnung I Gerhard Navratil

Form-Kennwerte • Schiefe: 3. Potenz der standardisierten Beobachtungswerte 3. standardisierte zentrale Moment • Wölbung (Kurtosis): 4. standardisierte zentrale Moment • Exzess: Ausgleichungsrechnung I Gerhard Navratil

Eigenschaften • Resistenz: Verhalten bei Ausreißern – Median hohe Resistenz, Mittelwert niedrige • Optimalitätseigenschaften: Lagekennwerte sollen die Datenmenge ‚optimal‘ repräsentieren erfüllte Kriterien: Ausgleichungsrechnung I Gerhard Navratil

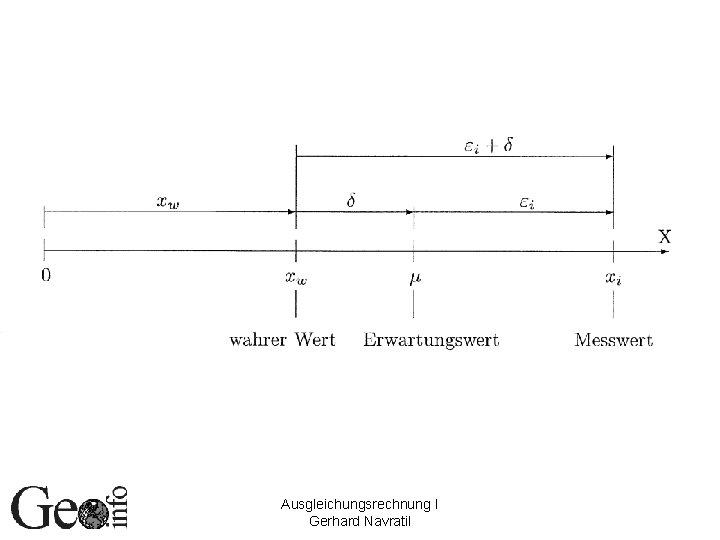
Statistische Begriffe in der Messtechnik (1) • Wahrer Wert: Tatsächlicher Wert des Merkmals (ist leider unbekannt, kann aber explizit vorgegeben sein – Winkelsumme) • Quasi-wahrer Wert: Hochgenaue Messung, deren Abweichung vom wahren Wert so gering ist, dass sie im vorliegenden Fall vernachlässigt werden kann (auch: richtiger Wert, Sollwert) • Erwartungswert: Mittelwert aller theoretisch möglichen Messwerte (Schätzwert: empirischer Mittelwert) Ausgleichungsrechnung I Gerhard Navratil

Statistische Begriffe in der Messtechnik (2) • Abweichung: Differenz Messgröße (Ist-Wert) – Bezugsgröße (Soll-Wert) • Wahre Abweichung: Bezugsgröße ist der wahre Wert Systematischer + zufälliger Anteil • Systematische Abweichungen: Mathematisches/physikalisches Modell nicht richtig • Zufällige Abweichungen: Nicht beherrschbare, nicht einseitig gerichtete Einflüsse (stochastische Einflüsse) • Grober Fehler: Irrtümer (durch Kontrollen eliminiert) Ausgleichungsrechnung I Gerhard Navratil

Ausgleichungsrechnung I Gerhard Navratil

Deskriptive Statistik im Vermessungswesen Unterschied systematische – zufällige Abweichungen schafft Probleme Elimination zufälliger Abweichungen durch Mittelbildung Elimination systematischer Einflüsse durch – Messanordnung (z. B. 2 Fernrohrlagen, Nivellement aus der Mitte) – rechnerische Korrektur (z. B. atmosphärische Korrekturen, Prismenkonstante) Annahme im weiteren Verlauf der Vorlesung: Keine systematischen Einflüsse vorhanden Ausgleichungsrechnung I Gerhard Navratil

Bekannter Erwartungswert Quasi-wahrer Wert m bekannt (z. B. Messung des Nullwinkels) Zufällige Abweichungen: ei = xi – m in Vektor e zusammengefasst Maß für die Streuung: (theoretische) Standardabweichung auch: mittlerer Fehler (Statistik: empirisch) Erwartungswert bekannt, ich verbrauche also keine Messung um einen Erwartungswert zu bestimmen. Ausgleichungsrechnung I Gerhard Navratil

Empirische Schätzung des Erwartungswertes Schätzwert für den Erwartungswert: arithmetisches Mittel Verbesserung Empirische Standardabweichung negative Abweichung Diesmal n-1, da wir den Schätzwert für den Erwartungswert bestimmen müssen! Ausgleichungsrechnung I Gerhard Navratil

Weitere Kennwerte • Arithmetisches Mittel der Verbesserungs. Absolutbeträge (durchschnittlicher Fehler) • Median der Verbesserungs-Absolutbeträge (wahrscheinlicher Fehler) • Bei großem n gilt: Ausgleichungsrechnung I Gerhard Navratil

Weitere übliche Fehlermaße • Relativer Fehler: Standardabweichung in Relation zur Messgröße z. B. Strecke von 1 km und s=5 mm • Helmert‘scher Punktlagefehler: Standardabweichung der Koordinaten bekannt: Ausgleichungsrechnung I Gerhard Navratil

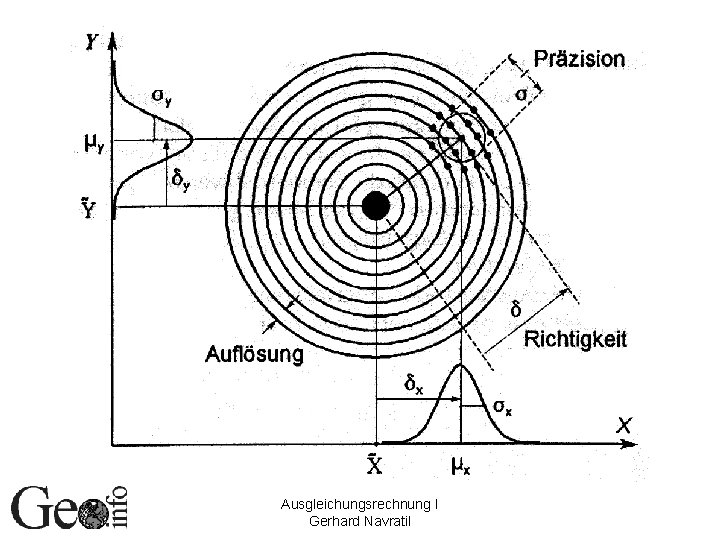
Genauigkeit – Präzision Richtigkeit • Genauigkeit: Wie genau stimmen die Messdaten mit dem Bezugswert überein? Zusammengesetzt aus Präzision (innere G. ) und Richtigkeit (äußere G. ) • Präzision: Wie gut ist die Wiederholbarkeit der Messungen? • Richtigkeit: Wie gut stimmen Erwartungswert und wahrer Wert überein? Ausgleichungsrechnung I Gerhard Navratil

Ausgleichungsrechnung I Gerhard Navratil

Zusammenfassung • Datenmengen werden mit Kenngrößen charakterisiert • Darstellung erfolgt meist graphisch (Histogramm oder Häufigkeitssummenkurve) • Oft wird eine Klasseneinteilung vorgenommen • Physikalische Größen haben einen unbekannten ‚wahren Wert‘ • Die Abweichungen werden Fehler genannt (zufällig, systematisch, grob) • Zufällige Fehler auch Verbesserungen Ausgleichungsrechnung I Gerhard Navratil