CSS 342 DATA STRUCTURES ALGORITHMS AND DISCRETE MATHEMATICS

CSS 342 DATA STRUCTURES, ALGORITHMS, AND DISCRETE MATHEMATICS I LECTURE 8. 161025 CUSACK CHAPT. 8, CARRANO APPENDIX E CARRANO C++ INTERLUDE 2, CHAPT 4, 6

Agenda • Finish Recursion • Dynamic Memory • Lab 3 • Induction • Hand back quiz

Typical types of recursion • Returns Value (n!, …) • Performs an action (adds to a string, … • Divides in half recursively (binary search, … • Tail Recursion • Backtracking (will introduce in future slides)

Costs of Recursion • Main cost of recursion is memory usage on stack • Stack v. Heap • • Compiler chooses where to allocate space from. Not always clear and compiler can make optimizations. Stack is per thread and limited. When space runs out: Stack Overflow. Function calls place locals, call parameters on stack Heap gets calls to malloc/free; new/delete generally on heap

Review: The Box Trace. Memory usage on thread stack! FIGURE 2 -5 BOX TRACE OF FACT(3) … CONTINUED Data Structures and Problem Solving with C++: Walls and Mirrors, Carrano and Henry, © 2013

Backtracking as a problem solving technique While (solution not complete) { if (in good state) “move forward guessing at solution” else “backtrack to last good state” } Often used in combination with Recursion

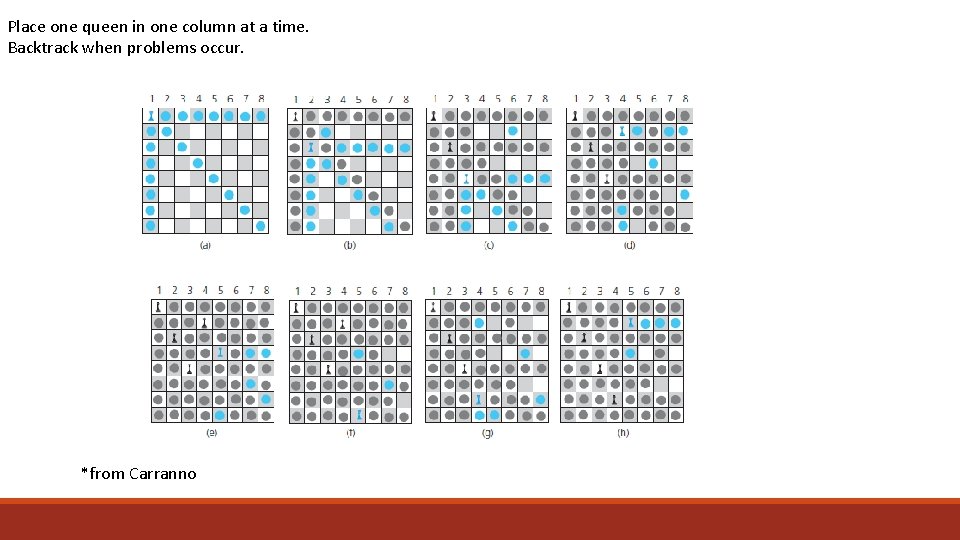
Backtrack: 8 queens problem Place 8 queens on a 8 * 8 chessboard so that no queen can attack any other queen. 7

Place one queen in one column at a time. Backtrack when problems occur. *from Carranno

8 Queens: Pseudo-code bool add. Queen(bool t[SIZE], int col) { if (col >= SIZE) { return true; } for (int row = 0; row < SIZE; row ++) { if (safe. Location(t, row, col)) { t[row][col] = true; if (add. Queen(t, col + 1)) { return true; } else { t[row][col] = false; } } } return false; } // place a new queen in the row // all the following cols were filled // A wrong position. Try the next row // all rows examined, but no candidates

Recursive Applications Discrete Mathematics (Combinatorics, Puzzles, Coding Theory) ◦ Tower of Hanoi and Gray Code Divide and Conquer ◦ Mergesort, Convex Hall, and Fast Fourier Transform Backtrack ◦ 8 Queens, Maze and Classic Chess Program Fractal Figures ◦ Koch, Sierpinski Allowhead, Gosper, Hilbert, and Dragon curves

Recursion w/Alice https: //www. youtube. com/watch? v=-3 Mcu 7 o 1 YSg (1: 32)

Dynamic Memory

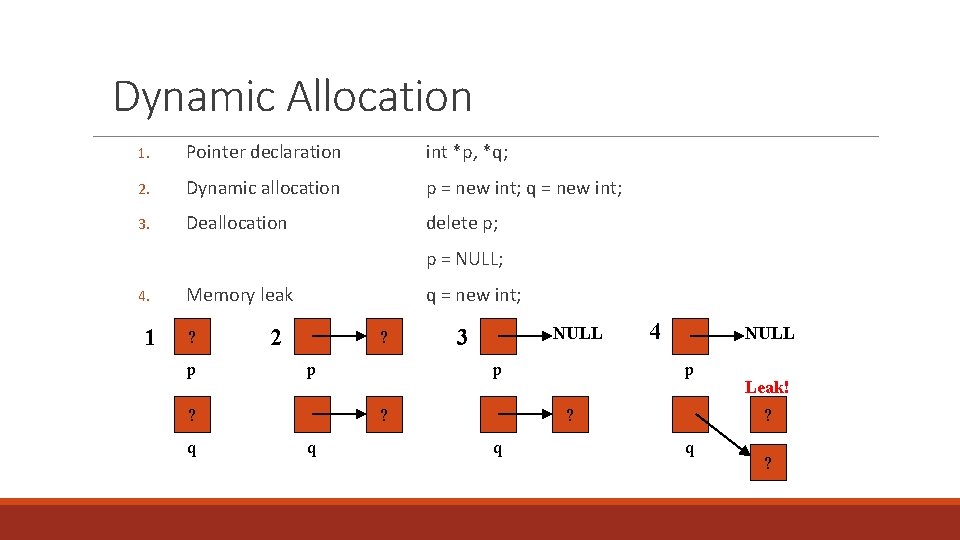
Dynamic Allocation 1. Pointer declaration int *p, *q; 2. Dynamic allocation p = new int; q = new int; 3. Deallocation delete p; p = NULL; 4. 1 Memory leak ? p q = new int; 2 ? p p ? ? q NULL 3 q 4 NULL p ? q Leak! ? q ?

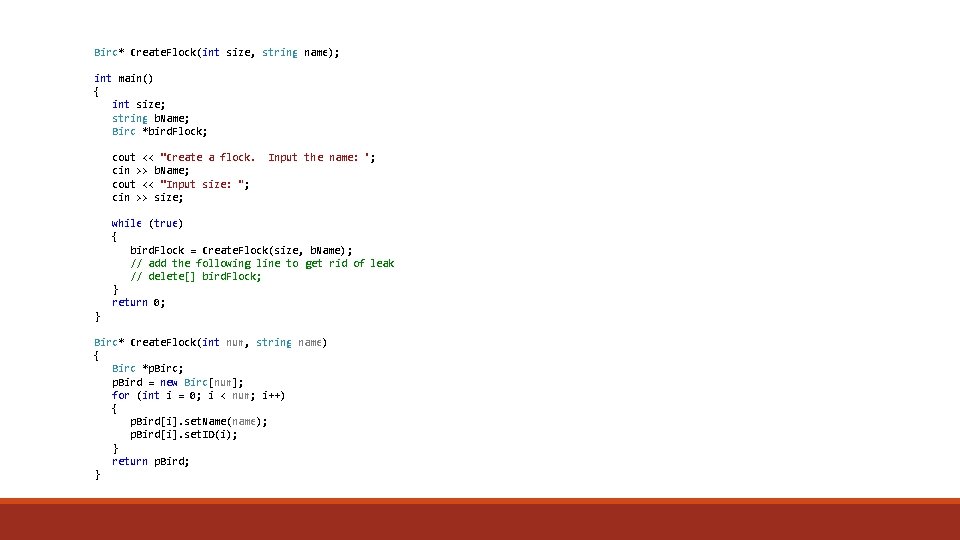
Bird* Create. Flock(int size, string name); int main() { int size; string b. Name; Bird *bird. Flock; cout << "Create a flock. cin >> b. Name; cout << "Input size: "; cin >> size; Input the name: "; while (true) { bird. Flock = Create. Flock(size, b. Name); // add the following line to get rid of leak // delete[] bird. Flock; } return 0; } Bird* Create. Flock(int num, string name) { Bird *p. Bird; p. Bird = new Bird[num]; for (int i = 0; i < num; i++) { p. Bird[i]. set. Name(name); p. Bird[i]. set. ID(i); } return p. Bird; }

Computer Scientist of the week Charles Babbage • Mathematician, Philosopher, Mechanical Engineer • Invented the first mechanical computer • Difference Engine: Computed values of polynomial functions • If completed at the time would have had 25000 parts • Finished in 1991 • Analytical Engine • Punch card based • Branching and looping supported • Currently being build: 7 Hz and 675 Bytes

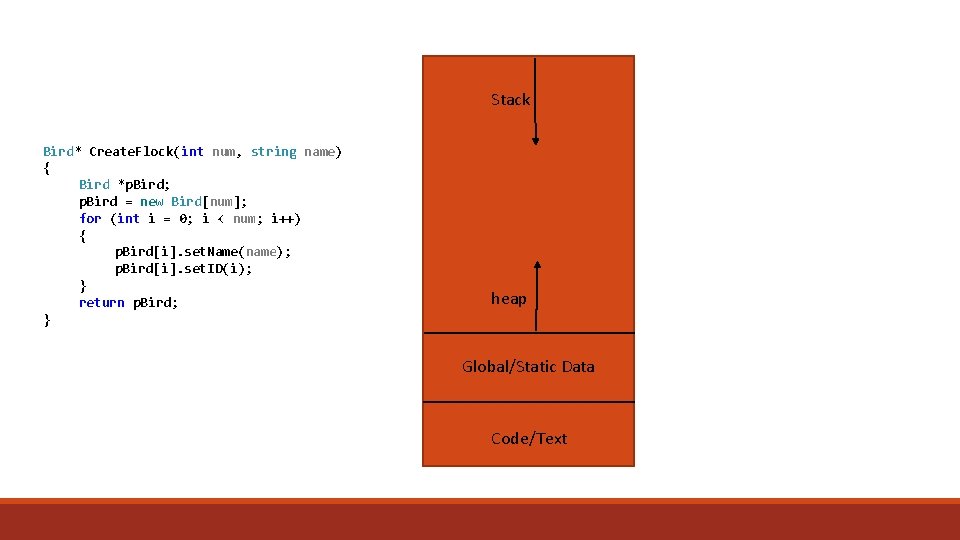
Stack Bird* Create. Flock(int num, string name) { Bird *p. Bird; p. Bird = new Bird[num]; for (int i = 0; i < num; i++) { p. Bird[i]. set. Name(name); p. Bird[i]. set. ID(i); } return p. Bird; } heap Global/Static Data Code/Text

Program 3 REVIEW

Quiz MEDIAN: 74

Grades Review Labs (5): Exams/Quizzes: http: //www. uwb. edu/registration/policies/grading-ug 35% 65%

Lab 1 • Rubric posted on Canvas • Did not take off points on style but comments show what was not followed. Will deduct points next time SCORE GRADE 86 -100 3. 5 -4 70 -85 2. 5 -3. 4 57 -69 2. 0 -2. 4 <57 <2. 0

Class Bell

In Class Code 1) Write a function which reverses the elements in an array. Input is the array and size of the array. 2) Do this in a way that does not use [ ] anywhere

Induction 1; N -> N+1

Induction Axiom: The principle of mathematical induction A property P(n) that involves an integer n is true for all n ≥ 0 if the following are true: 1. P(0) is true. 2. If P(k) is true for any k ≥ 0, then P(k+1) is true.

Some history* *from our good friends at Wickapedia

Proof by Induction for n x Write a recursive function which calculates xn Prove the correctness of the recursive solution using induction int pow(int x, int n) { if (n == 0) return 1; else return x * pow(x, n-1); }

Proof by Induction for 1. Basis: 2. Inductive hypothesis: 3. 4. n x When n = 0, pow(x, 0) = 1. x 0 = 1. The recursive function is correct. When n = k, assume that pow(x, k) is correct, i. e. , xk. Inductive step: Show the pow(x, k+1) is correct. pow(x, k+1) = x * pow(x, k) By the inductive hypothesis, pow(x, k) returns the value xk. Thus, pow(x, k+1) = x * xk = xk+1 If pow(x, k) is correct, pow(x, k+1) is correct. Therefore, by the principle of mathematical induction, pow(x, n) is correct for any n ≥ 1.

Prove: a+ar 1+ar 2+ar 3+ … +arn =a(rn+1 – 1)/(r-1)

Strong Form of Mathematical Induction A property P(n) that involves an integer n is true for all n ≥ 0 if the following are true: 1. 2. P(0) is true. If P(0), P(1), …, P(k) are true for any k ≥ 0, then P(k+1) is true. Difference from ordinary form of mathematical induction: P(k+1) is factorized in a combination of two or more of P(0) through to P(k). Proof by strong form of mathematical induction 1. 2. I. II. Base case or (basis): prove P(0) is true. Inductive step: Inductive hypothesis: Assume P(1), P(2), . . , P(k) is true for any k ≥ 0 Inductive conclusion: Prove P(k+1) is true.

Prove using induction: Every Integer > 1 Can Be Written as a Product of Prime Integers 1. Basis: n = 2. 2 is a prime number itself, and thus can be written as a product of prime integers. The proposition is true. 2. Strong Inductive hypothesis: Assume that the proposition is true for each of the integers 2, 3, … k 3. Inductive step: Show the proposition is true for k + 1. If k + 1 is a prime number, there is nothing more to show. If k + 1 is NOT a prime number, k + 1 is divisible and can be written k + 1= x * y where 1 < x < k + 1 and 1 < y < k + 1 Notice that x and y can be written as a product of prime integers by inductive hypothesis. If k is a product of prime numbers, k+1 is a product of prime numbers. Therefore, by the principle of mathematical induction, the proposition is true when n ≥ 1.