CSE 554 Lecture 9 Laplacian Deformation Fall 2016

CSE 554 Lecture 9: Laplacian Deformation Fall 2016 CSE 554 Laplacian Deformation Slide 1

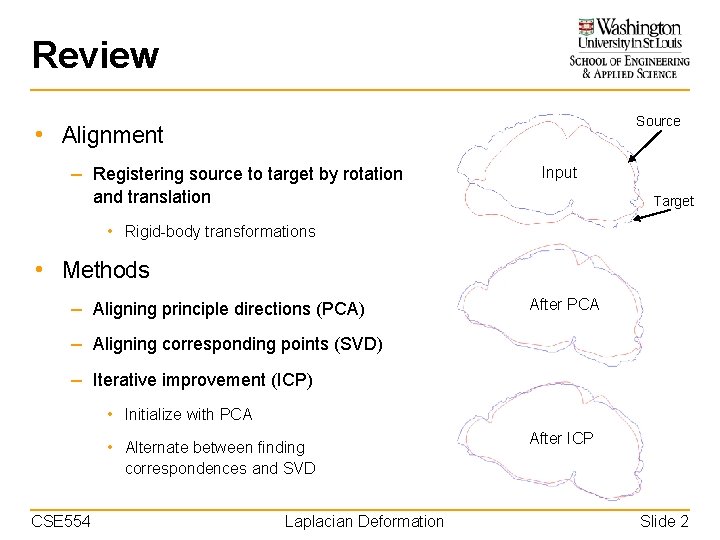
Review Source • Alignment – Registering source to target by rotation Input and translation Target • Rigid-body transformations • Methods – Aligning principle directions (PCA) After PCA – Aligning corresponding points (SVD) – Iterative improvement (ICP) • Initialize with PCA • Alternate between finding After ICP correspondences and SVD CSE 554 Laplacian Deformation Slide 2

Non-rigid Registration • Rigid alignment cannot account for shape variance • Non-rigid deformation is needed for improved fitting Source Target Rigid alignment CSE 554 After non-rigid deformation Laplacian Deformation Slide 3

Non-rigid Registration • A minimization problem – Minimizing the distance between the deformed source and the target • “Fitting term” – Minimizing the distortion to the source shape • “Distortion term” CSE 554 Laplacian Deformation Slide 4

Intrinsic vs. Extrinsic • Intrinsic methods – Deforms points on the source curve/surface – App: boundary curve or surface matching • Extrinsic methods – Deforms all points in the space around the source curve/surface – App: image or volume matching CSE 554 Laplacian Deformation Slide 5

Intrinsic Registration Target • Given a source and target shape – Plus correspondences between some source points (called handles) and target points Handle • Relocate source points such that: – The handles move to their corresponding targets (fitting term) – The rest of the shape deforms as naturally as possible (distortion term) • ICP-style registration – Alternate between finding correspondences (e. g. , closest neighbors) and deformation CSE 554 Laplacian Deformation Slide 6

Laplacian-based Deformation • An intrinsic method used in graphics/animation – Simple and efficient (fitting/distortion terms are quadratic) – Preserving local shape features Reference: “Laplacian surface editing”, by Sorkine et al. , 2004 CSE 554 Laplacian Deformation Slide 7

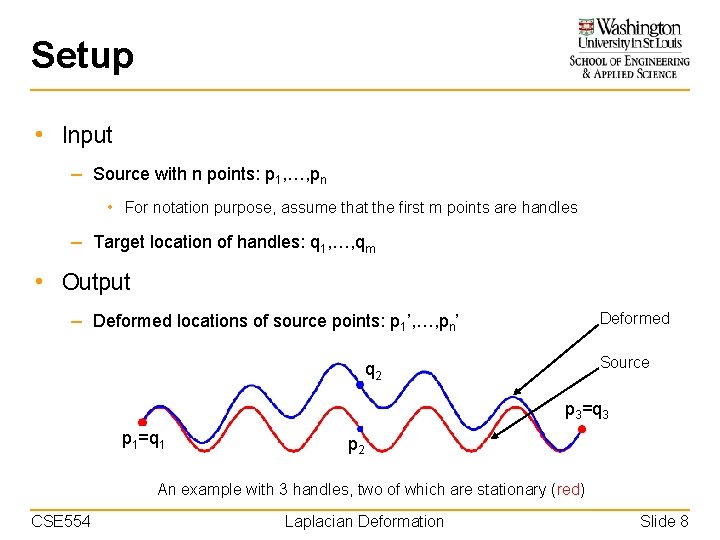
Setup • Input – Source with n points: p 1, …, pn • For notation purpose, assume that the first m points are handles – Target location of handles: q 1, …, qm • Output – Deformed locations of source points: p 1’, …, pn’ Deformed Source q 2 p 3=q 3 p 1=q 1 p 2 An example with 3 handles, two of which are stationary (red) CSE 554 Laplacian Deformation Slide 8

Overview • Finding deformed locations pi’ that minimize: – Ef: fitting term • Measures how close are the deformed handles to the target – Ed: distortion term • Measures how much the source shape is changed CSE 554 Laplacian Deformation Slide 9

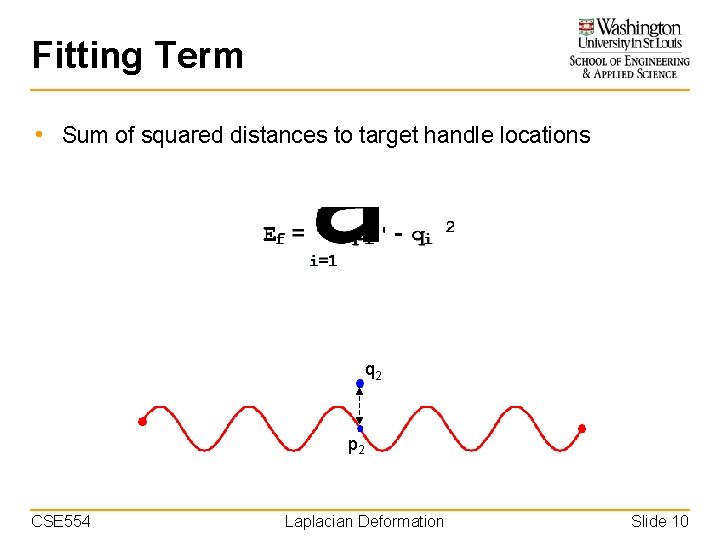
Fitting Term • Sum of squared distances to target handle locations q 2 p 2 CSE 554 Laplacian Deformation Slide 10

Distortion Term • Q: How to measure shape locally? • A: By “bumpiness” at each vertex – Laplacian: vector from the centroid of neighbors to the vertex • A linear operator over point locations where Ni are indices of neighboring vertices of pi • Recall that in fairing, we minimizes this vector to “smooth out” bumps CSE 554 Laplacian Deformation Slide 11

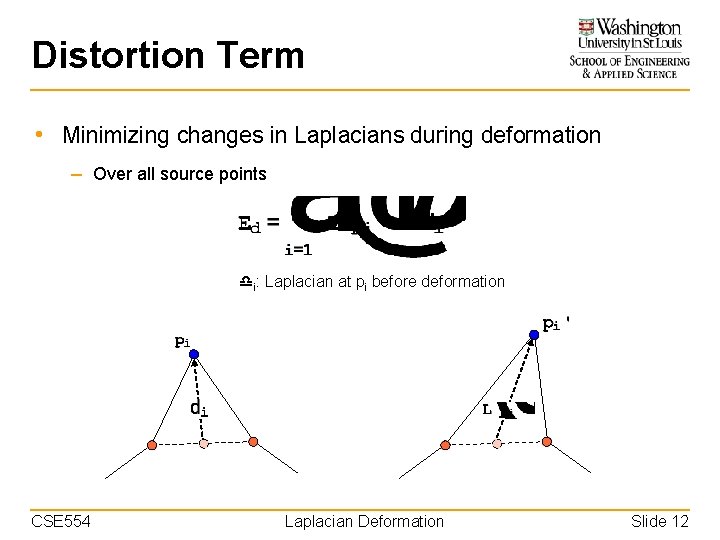
Distortion Term • Minimizing changes in Laplacians during deformation – Over all source points i: Laplacian at pi before deformation CSE 554 Laplacian Deformation Slide 12

Putting Together • Finding deformed locations pi’ that minimize: – A quadratic equation in terms of variables (pix’, piy’, piz’) • qi, i are constants • L[] is a linear operator CSE 554 Laplacian Deformation Slide 13

Quadratic Minimization • A general form of quadratic minimization: – There are s variables: x=(x 1, …, xs)T – Each a 1, …, ak is a length-s column vector (linear coefficients) – Each b 1, …, bk is a scalar (constant coefficients) – k should be greater than s (so that the problem is over-constrained) CSE 554 Laplacian Deformation Slide 14

Quadratic Minimization • Re-writing our minimization in the general form – In 2 D, there are s=2 n variables: x = (p 1 x’, …, pnx’, p 1 y’, …, pny’ )T • In 3 D, there are s=3 n variables – We will next re-write each quadratic term in 2 D as (aix-bi)2 • Can be extended easily to 3 D CSE 554 Laplacian Deformation Slide 15

Quadratic Minimization • The ai and bi in the fitting term – There are 2 m quadratic terms – In the first set of m terms: • For i=1, …, m, bi=qix, ai contains all zero, except its (i)th entry is 1. – In the second set of m terms: • For i=1, …, m, bi+m=qiy, ai+m contains all zero, except its (i+n)th entry is 1 CSE 554 Laplacian Deformation Slide 16

Quadratic Minimization • The ai and bi in the fitting term – There are 2 m quadratic terms – Example with 3 vertices and 2 fitting constraints (n=3; m=2): CSE 554 Laplacian Deformation Slide 17

Quadratic Minimization • The ai and bi in the distortion term: – There are 2 n quadratic terms – The first set of n terms: • For i=1, …, n, ai is all zero except the (i)th entry is 1, the (j)th entries are -1/|Ni| for all j Ni, and bi= ix – The second set of n terms: • For i=1, …, n, ai+n is all zero except the (i+n)th entry is 1, the (j+n)th entries are -1/|Ni| for all j Ni, and bi+n= iy CSE 554 Laplacian Deformation Slide 18

Quadratic Minimization • The ai and bi in the distortion term: – There are 2 n quadratic terms – Example with 3 vertices (n=3): CSE 554 Laplacian Deformation Slide 19

Quadratic Minimization • To solve: • Re-write in matrix form: where is a k by s matrix is a length-k vector CSE 554 Laplacian Deformation Slide 20

Quadratic Minimization • The minimizer is where the partial derivatives are all zero – To solve for x in this equation: • Taking matrix inverse (good for small s, but numerically unstable for large s) • Using specialized linear system solver (Linear. Solve in Mathematica, Eigen/TNT/LAPACK in C) CSE 554 Laplacian Deformation Slide 21

Summary • Compute Laplacians ( i) • Construct coefficients (ai, bi) – Put them into matrices (A, B) • Solve (x) – CSE 554 Laplacian Deformation Slide 22

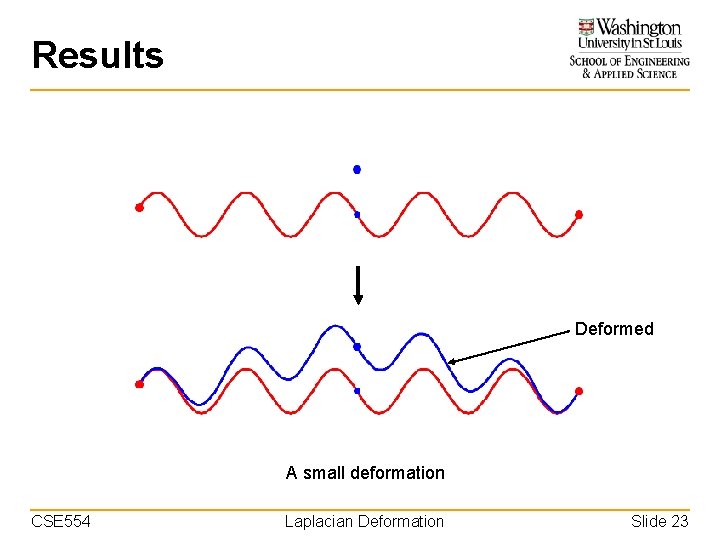
Results Deformed A small deformation CSE 554 Laplacian Deformation Slide 23

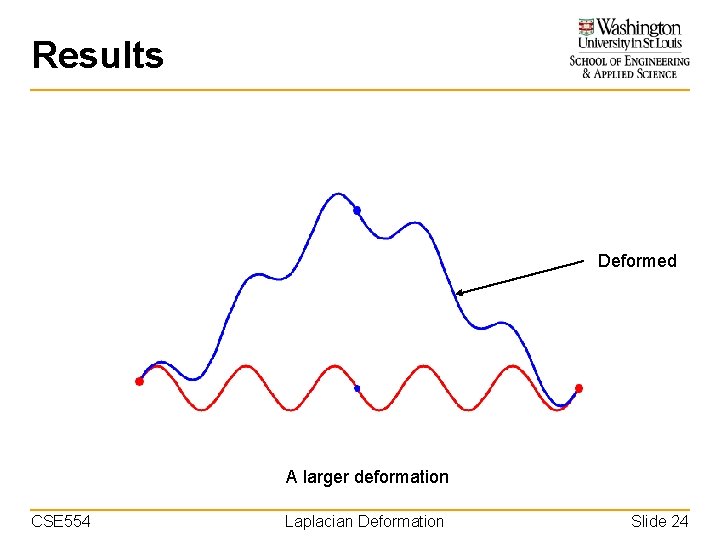
Results Deformed A larger deformation CSE 554 Laplacian Deformation Slide 24

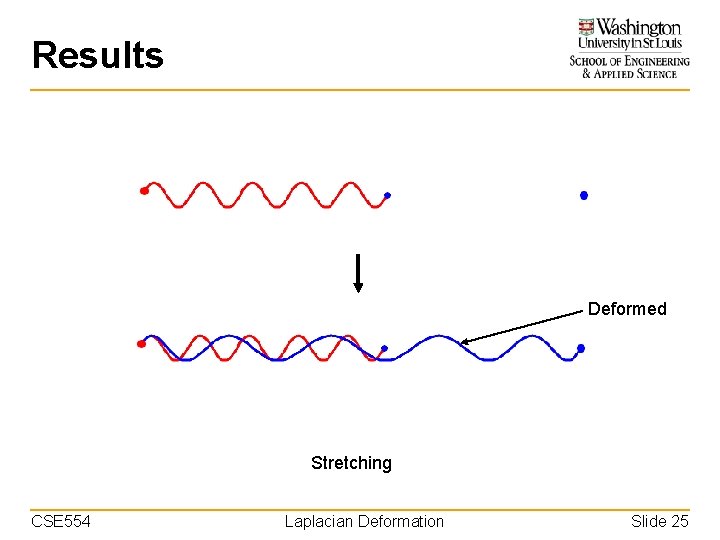
Results Deformed Stretching CSE 554 Laplacian Deformation Slide 25

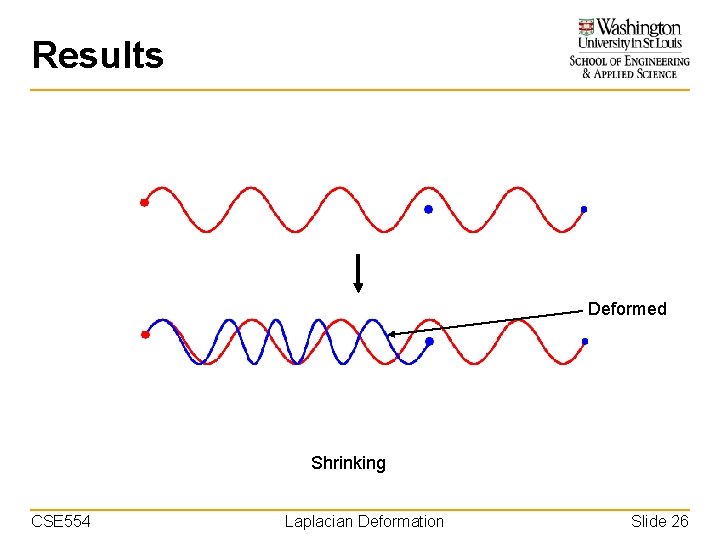
Results Deformed Shrinking CSE 554 Laplacian Deformation Slide 26

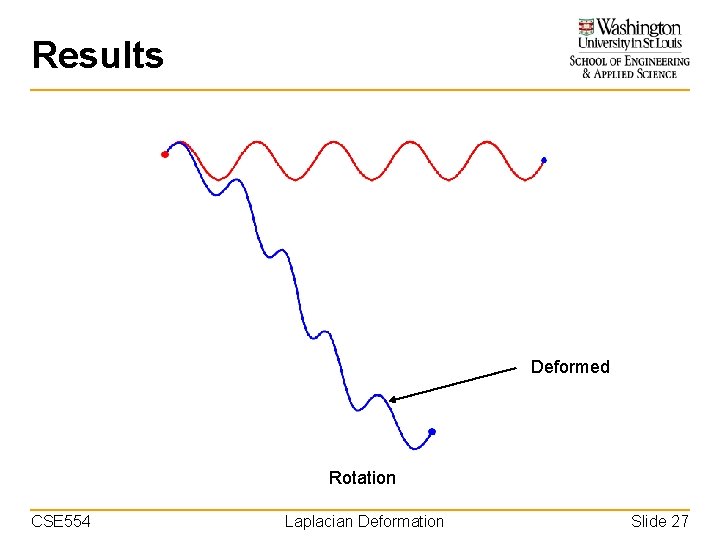
Results Deformed Rotation CSE 554 Laplacian Deformation Slide 27

Discussion • Limitations – Local features don’t rotate or scale with the model • Reason: Laplacian is not invariant under rotation or scale – Two bumps that differ by rotation or scale result in non-zero distortion CSE 554 Laplacian Deformation Slide 28

A Better Distortion Term • Not penalizing rotation and scaling of local features – Estimating how the local neighborhood is transformed – Transforming the original Laplacian vectors before comparing to the deformed Laplacians CSE 554 Laplacian Deformation Slide 29

Catch 22 • Q: How do we find Ti before we know the deformed shape? • A: Represent Ti as a function of the unknown variables – A linear function of pi’, just like L • We will focus in the derivations of the 2 D case – 3 D results will be briefly presented at the end CSE 554 Laplacian Deformation Slide 30

Transformation Matrices (2 D) • Homogeneous coordinates – A 2 D point: (x, y, 1) • A 2 D vector: (x, y, 0) – A 3 D point: (x, y, z, 1) • A 3 D vector: (x, y, z, 0) CSE 554 Laplacian Deformation Slide 31

Transformation Matrices (2 D) • Translation – Cartesian coordinates: vector addition – Homogeneous coordinates: matrix product CSE 554 Laplacian Deformation Slide 32

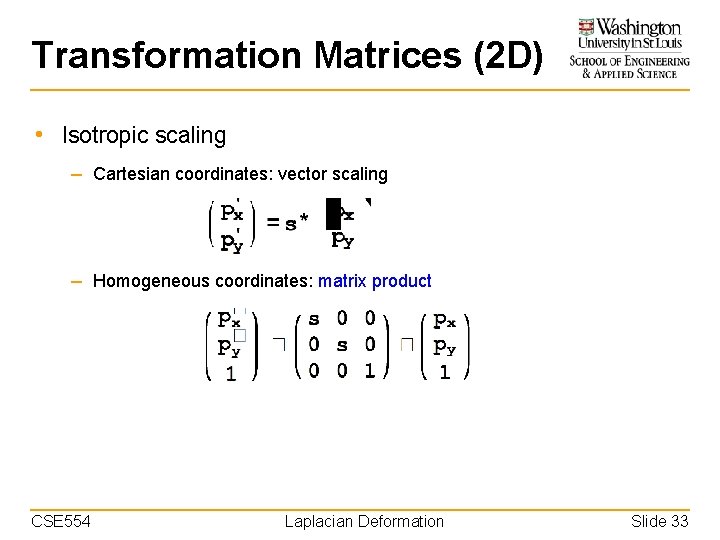
Transformation Matrices (2 D) • Isotropic scaling – Cartesian coordinates: vector scaling – Homogeneous coordinates: matrix product CSE 554 Laplacian Deformation Slide 33

Transformation Matrices (2 D) • Rotation – Cartesian coordinates: matrix product – Homogeneous coordinates: matrix product CSE 554 Laplacian Deformation Slide 34

Transformation Matrices (2 D) • Summary of elementary similarity transformations – To perform a sequence of transformations: multiple the corresponding matrices in order Translation by vector v Scaling by scalar s Rotation by angle CSE 554 Laplacian Deformation Slide 35

Similarity Transforms (2 D) • General similarity transformations – The product of any set of similarity matrices can be written this way – Any choice of (a, w, tx, ty) can be written as a sequence of rotation, isotropic scaling and translation • Note that a and w can’t be both zero CSE 554 Laplacian Deformation Slide 36

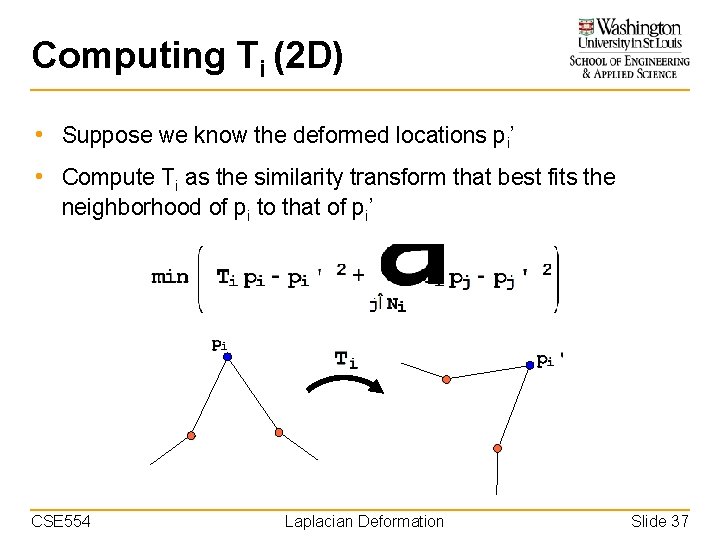
Computing Ti (2 D) • Suppose we know the deformed locations pi’ • Compute Ti as the similarity transform that best fits the neighborhood of pi to that of pi’ CSE 554 Laplacian Deformation Slide 37

Computing Ti (2 D) • Suppose we know the deformed locations pi’ • Compute Ti as the similarity transform that best fits the neighborhood of pi to that of pi’ • This is a quadratic minimization problem for entries of Ti – E. g. , a, w, tx, ty CSE 554 Laplacian Deformation Slide 38

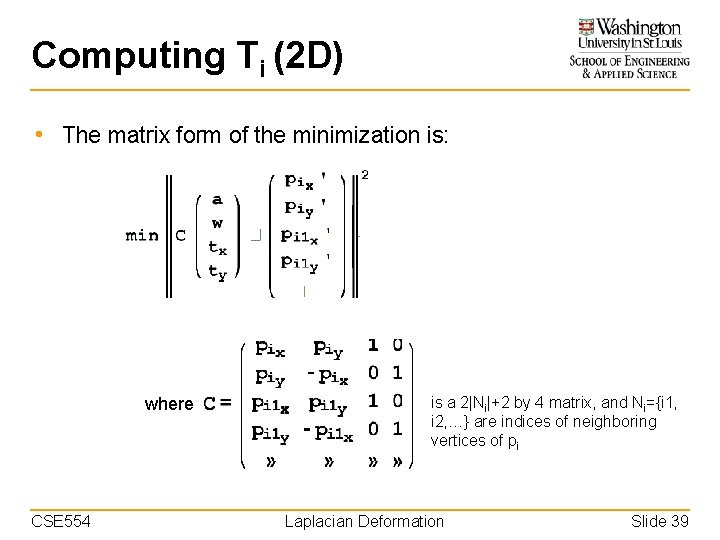
Computing Ti (2 D) • The matrix form of the minimization is: where CSE 554 is a 2|Ni|+2 by 4 matrix, and Ni={i 1, i 2, …} are indices of neighboring vertices of pi Laplacian Deformation Slide 39

Computing Ti (2 D) • By quadratic minimization: – Linear expressions of variables (pix’ , piy’) CSE 554 Laplacian Deformation Slide 40

Distortion Term (2 D) • Two parts of each distortion term: – Transformed Laplacian: where – Laplacian of the deformed locations: where CSE 554 Laplacian Deformation is a 2 by 2|Ni|+2 matrix Slide 41

Distortion Term (2 D) • Putting together: where and are its rows – They form 2 n quadratic terms (aix-bi)2 for x = (p 1 x’, …, pnx’, p 1 y’, …, pny’ )T • All bi are zero • Each ai can be extracted from H CSE 554 Laplacian Deformation Slide 42

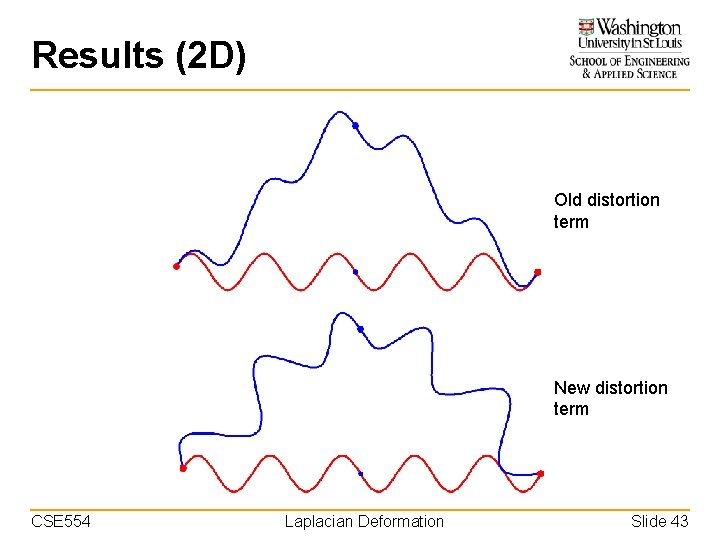
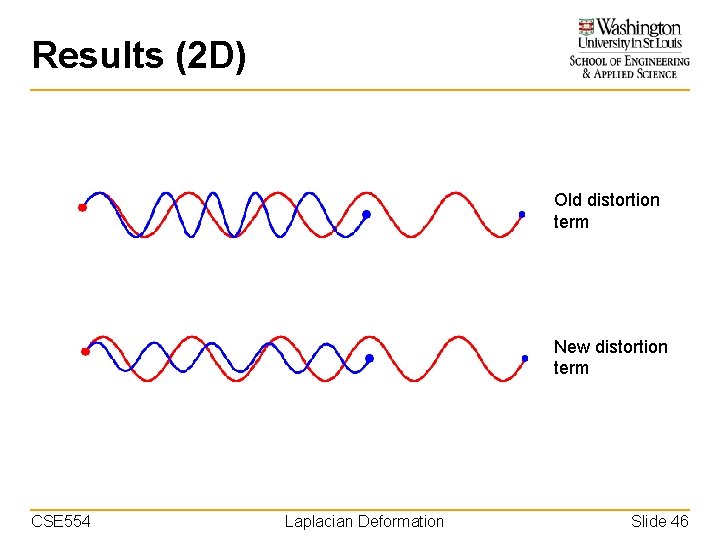
Results (2 D) Old distortion term New distortion term CSE 554 Laplacian Deformation Slide 43

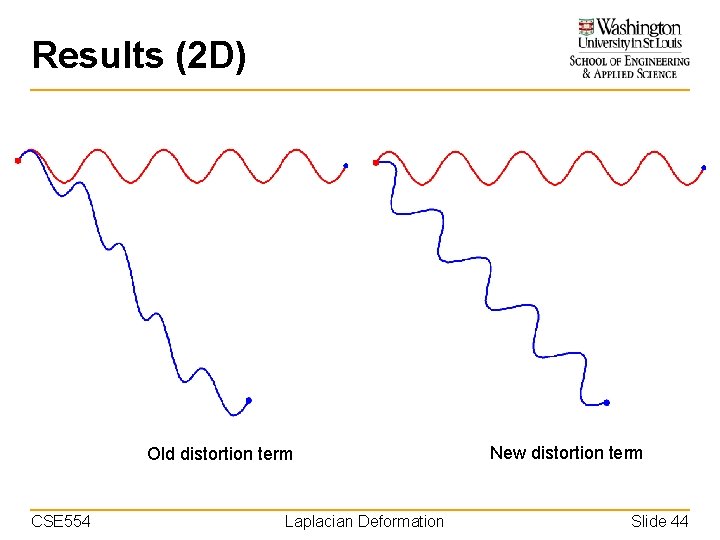
Results (2 D) Old distortion term CSE 554 Laplacian Deformation New distortion term Slide 44

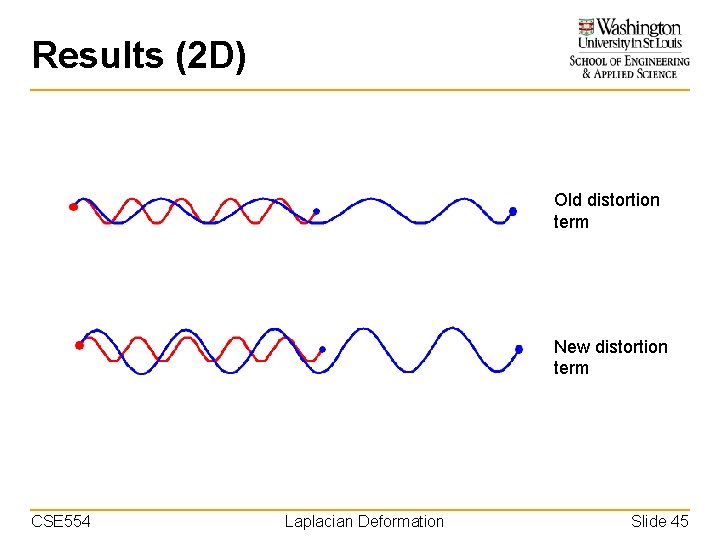
Results (2 D) Old distortion term New distortion term CSE 554 Laplacian Deformation Slide 45

Results (2 D) Old distortion term New distortion term CSE 554 Laplacian Deformation Slide 46

Registration • Use nearest neighbors as corresponding target locations – Assuming the source is already close to the target • Iterative closest point (ICP) – 1. For each point on the source pi, treat it as a handle, and assign its closest point on the target as its target location qi. – 2. Compute Laplacian-based deformation. – 3. Repeat step (1) until a termination criteria is met. CSE 554 Laplacian Deformation Slide 47

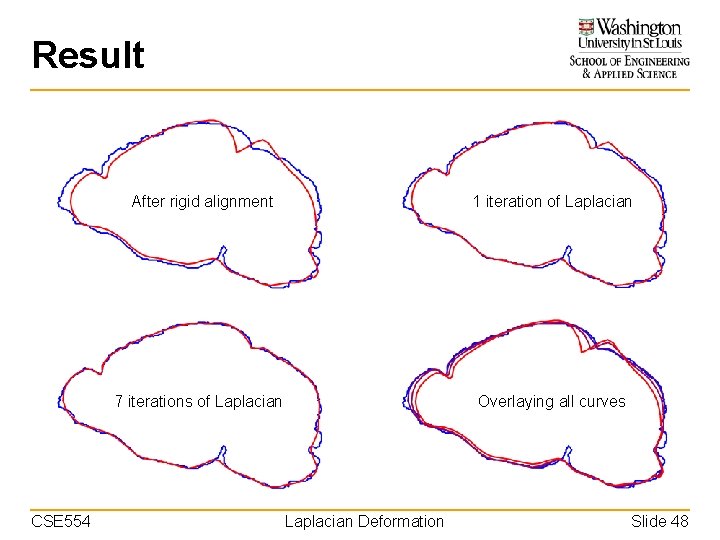
Result CSE 554 After rigid alignment 1 iteration of Laplacian 7 iterations of Laplacian Overlaying all curves Laplacian Deformation Slide 48

Result • Weighting the distortion term large w medium w small w CSE 554 Laplacian Deformation Slide 49

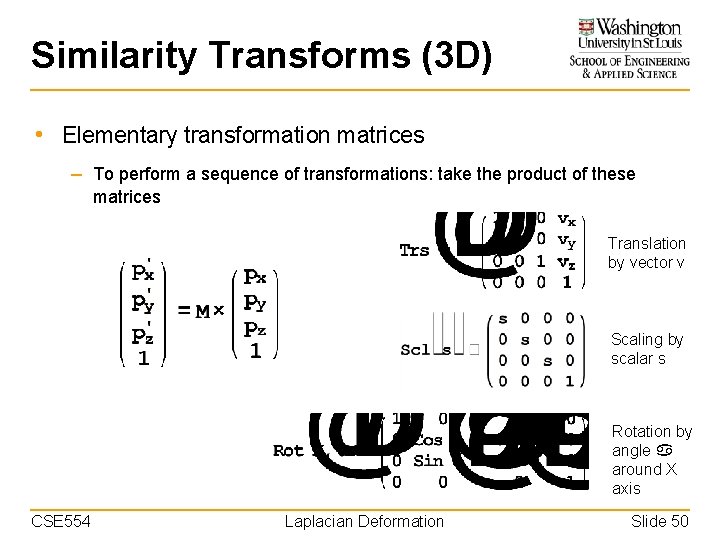
Similarity Transforms (3 D) • Elementary transformation matrices – To perform a sequence of transformations: take the product of these matrices Translation by vector v Scaling by scalar s Rotation by angle around X axis CSE 554 Laplacian Deformation Slide 50

Similarity Transforms (3 D) • General similarity transformations in 3 D – Approximates the product of a set of elementary matrices • Up to a small rotation angle • May introduce skewing for large rotations CSE 554 Laplacian Deformation Slide 51

Computing Ti (3 D) • Assuming known deformation, by quadratic minimization: where – Linear expressions of the deformed points pi’ • C is a 3|Ni|+3 by 7 matrix CSE 554 Laplacian Deformation Slide 52

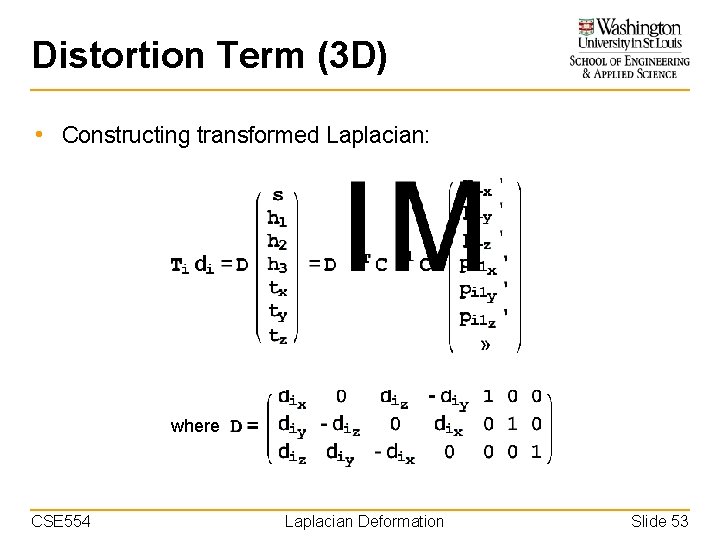
Distortion Term (3 D) • Constructing transformed Laplacian: where CSE 554 Laplacian Deformation Slide 53