Hookes Law Hookes law elastic limit experimental investigations

Hooke’s Law

Hooke’s law, elastic limit, experimental investigations. F = kΔL Tensile strain and tensile stress. Elastic strain energy, breaking stress. Derivation of energy stored =1/2 FΔL

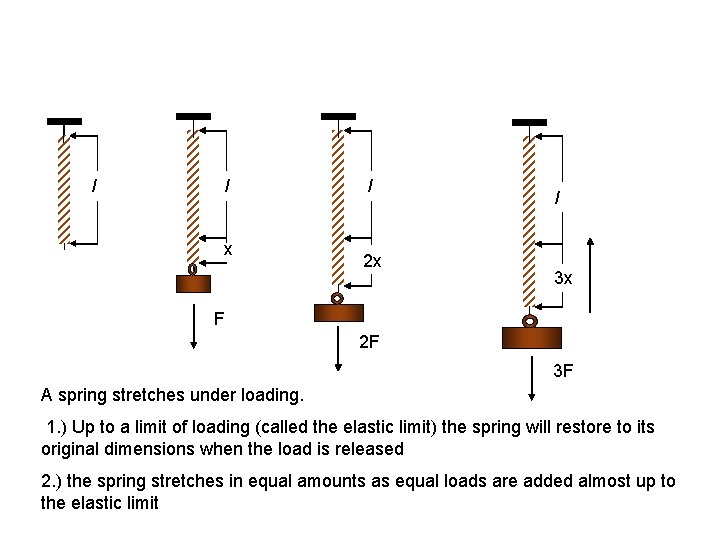
l l x l 2 x l 3 x F 2 F 3 F A spring stretches under loading. 1. ) Up to a limit of loading (called the elastic limit) the spring will restore to its original dimensions when the load is released 2. ) the spring stretches in equal amounts as equal loads are added almost up to the elastic limit

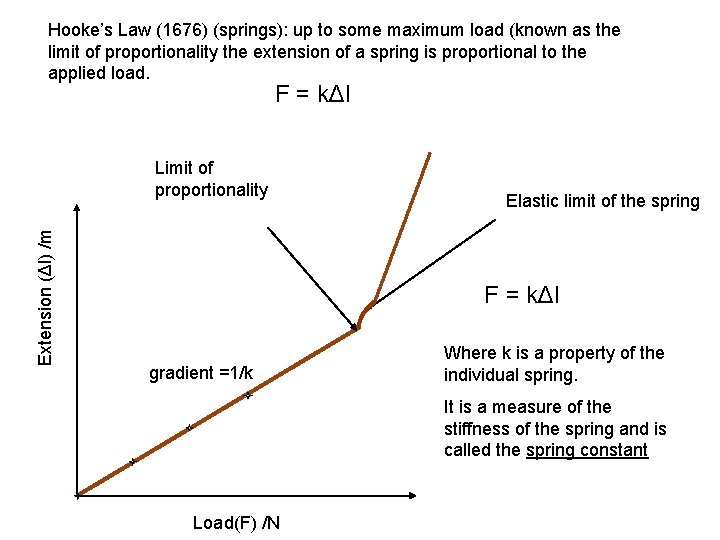
Hooke’s Law (1676) (springs): up to some maximum load (known as the limit of proportionality the extension of a spring is proportional to the applied load. F = kΔl Extension (Δl) /m Limit of proportionality Elastic limit of the spring F = kΔl gradient =1/k Where k is a property of the individual spring. It is a measure of the stiffness of the spring and is called the spring constant Load(F) /N

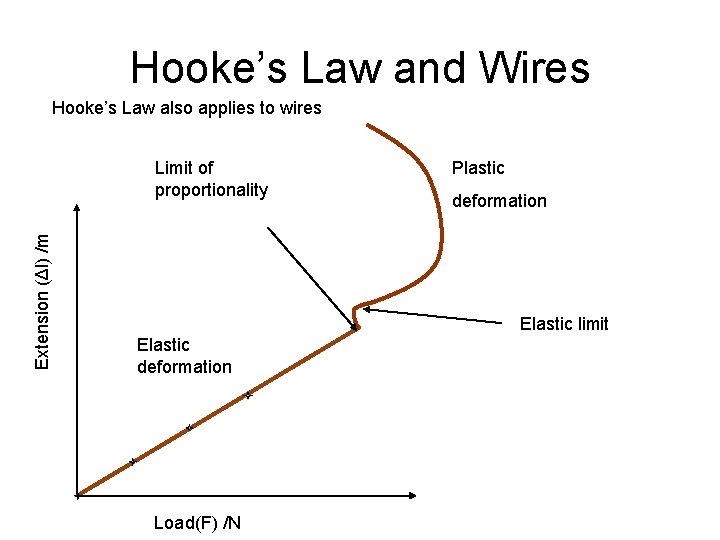
Hooke’s Law and Wires Hooke’s Law also applies to wires Extension (Δl) /m Limit of proportionality Plastic deformation Elastic limit Elastic deformation Load(F) /N

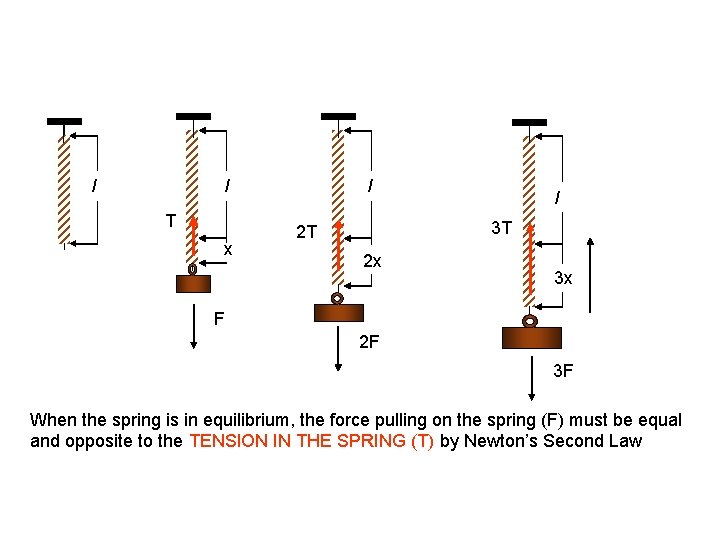
l l T x l l 3 T 2 T 2 x 3 x F 2 F 3 F When the spring is in equilibrium, the force pulling on the spring (F) must be equal and opposite to the TENSION IN THE SPRING (T) by Newton’s Second Law

Tensile Stress and Tensile Strain

Tensile Stress • It is important to be able to compare the properties of materials of different cross sectional area • The use of the simple idea of the force applied to a wire does not do this. A A A F F F We need to take about the force per unit of cross sectional area. This is called the stress. We are interested in the pulling stress or TENSILE STRESS Units; Nm-2

Tensile Strain • In a similar way, just to talk about the extension under load tells us nothing if we are trying to compare wires of different lengths • We need an idea that takes different lengths of wire into account. Tensile strain is the ratio change in length Original length Tensile strain has no units

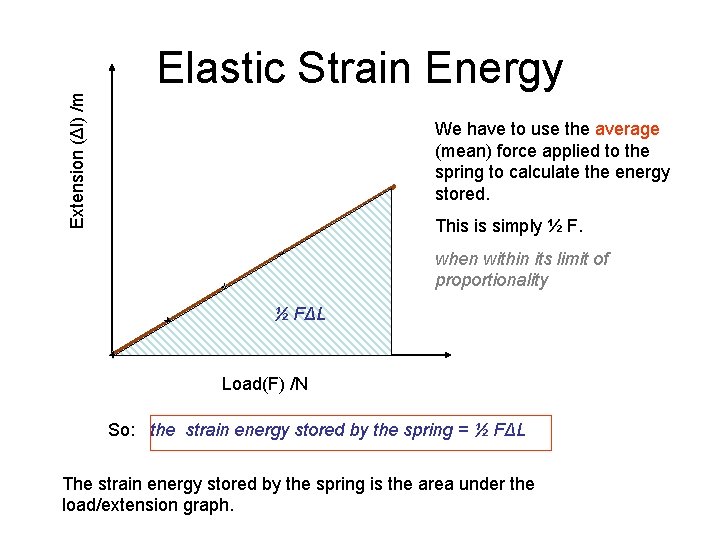
Elastic Strain Energy • When a spring is stretched, work is done on the spring. (effectively we are changing the gravitational potential energy of the load into elastic strain energy within the spring) • The work done has to be equal to the force x the displacement (i. e. the distance moved in the direction of the force) ΔL W=Fd • However the force on the spring is not constant it is increasing. F

Extension (Δl) /m Elastic Strain Energy We have to use the average (mean) force applied to the spring to calculate the energy stored. This is simply ½ F. when within its limit of proportionality ½ FΔL Load(F) /N So: the strain energy stored by the spring = ½ FΔL The strain energy stored by the spring is the area under the load/extension graph.

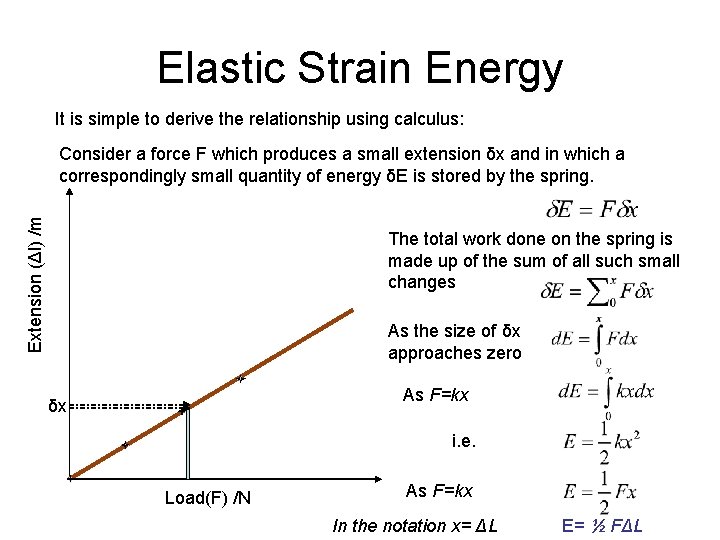
Elastic Strain Energy It is simple to derive the relationship using calculus: Extension (Δl) /m Consider a force F which produces a small extension δx and in which a correspondingly small quantity of energy δE is stored by the spring. The total work done on the spring is made up of the sum of all such small changes As the size of δx approaches zero As F=kx δx i. e. Load(F) /N As F=kx In the notation x= ΔL E= ½ FΔL

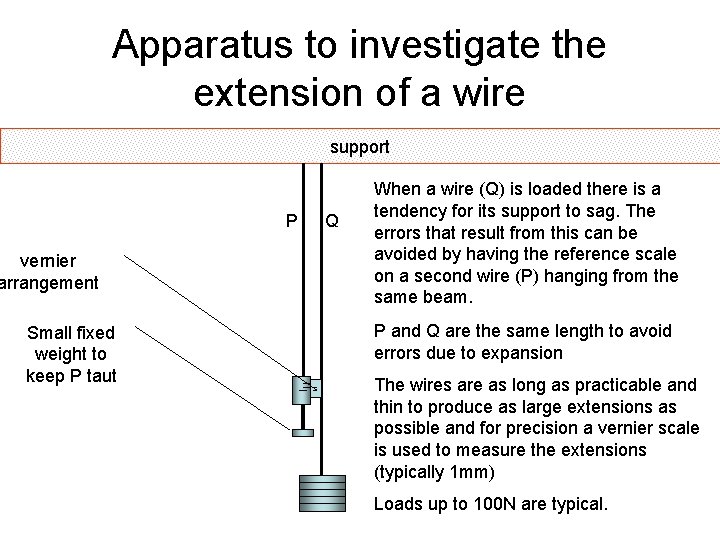
Apparatus to investigate the extension of a wire support P vernier arrangement Small fixed weight to keep P taut Q When a wire (Q) is loaded there is a tendency for its support to sag. The errors that result from this can be avoided by having the reference scale on a second wire (P) hanging from the same beam. P and Q are the same length to avoid errors due to expansion The wires are as long as practicable and thin to produce as large extensions as possible and for precision a vernier scale is used to measure the extensions (typically 1 mm) Loads up to 100 N are typical.

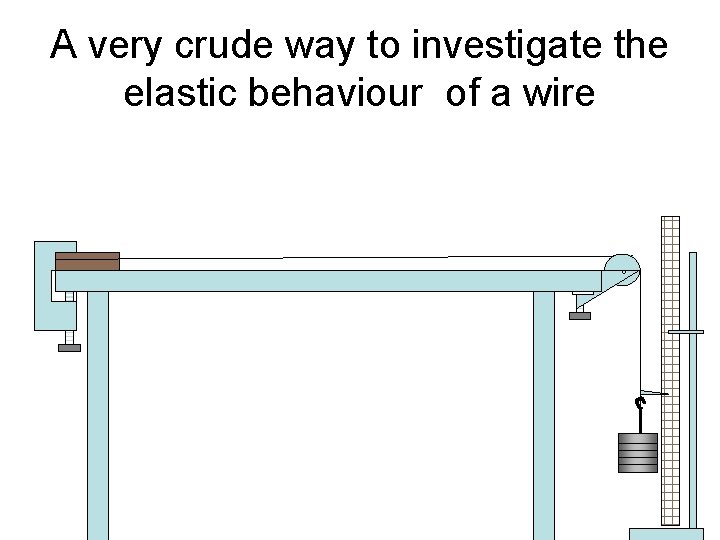
A very crude way to investigate the elastic behaviour of a wire