CSE 326 Data Structures Lecture 19 Disjoint Sets









![Weighted Union Code typedef ID int; ID union(ID x, ID y) { assert(up[x] == Weighted Union Code typedef ID int; ID union(ID x, ID y) { assert(up[x] ==](https://slidetodoc.com/presentation_image_h2/83eb6ad07bc6932fb6a34573967225f3/image-29.jpg)





- Slides: 36

CSE 326: Data Structures Lecture #19 Disjoint Sets Dynamic Equivalence Weighted Union & Path Compression David Kaplan davek@cs

Today’s Outline • • Making a “good” maze Disjoint Set Union/Find ADT Up-trees Maze revisited Weighted Union Path Compression An amazing complexity analysis

The Maze Construction Problem • Represent maze environment as graph {V, E} – collection of rooms: V – connections between rooms (initially all closed): E • Construct a maze: – collection of rooms: V = V – designated rooms in, i V, and out, o V – collection of connections to knock down: E E such that one unique path connects every two rooms

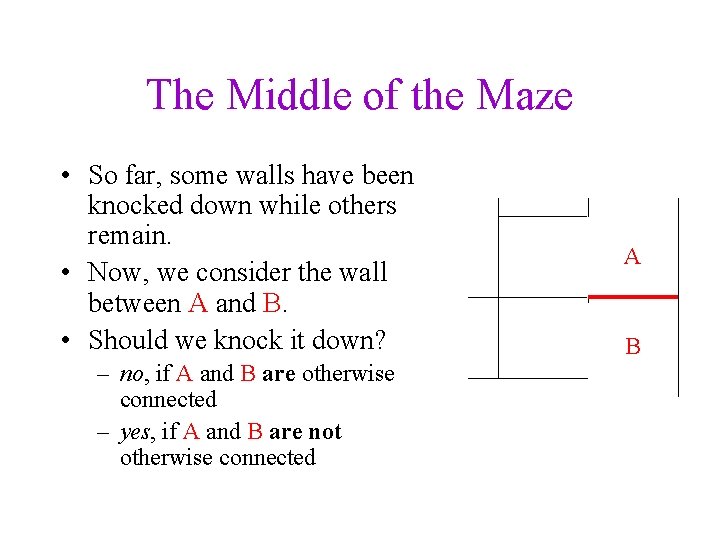
The Middle of the Maze • So far, some walls have been knocked down while others remain. • Now, we consider the wall between A and B. • Should we knock it down? – no, if A and B are otherwise connected – yes, if A and B are not otherwise connected A B

Maze Construction Algorithm While edges remain in E u Remove a random edge e = (u, v) from E v If u and v have not yet been connected - add e to E - mark u and v as connected

Equivalence Relations An equivalence relation R has three properties: – reflexive: for any x, x. Rx is true – symmetric: for any x and y, x. Ry implies y. Rx – transitive: for any x, y, and z, x. Ry and y. Rz implies x. Rz Connection between rooms is an equivalence relation (call it C) For any rooms a, b, c a C a (A room connects to itself!) If a C b, then b C a If a C b and b C c, then a C c Examples of other equivalence relations?

Disjoint Set Union/Find ADT • Union/Find operations – – create destroy union find(4) {1, 4, 8} 8 {6} {7} {2, 3, 6} {5, 9, 10} union(2, 6) {2, 3} • Disjoint set equivalence property: every element of a DS U/F structure belongs to exactly one set • Dynamic equivalence property: the set of an element can change after execution of a union

Disjoint Set Union/Find More Formally Given a set U = {a 1, a 2, … , an} Maintain a partition of U, a set of subsets of U {S 1, S 2, … , Sk} such that: - each pair of subsets Si and Sj are disjoint: - together, the subsets cover U: - The Si are mutually exclusive and collectively exhaustive Union(a, b) creates a new subset which is the union of a’s subset and b’s subset Find(a) returns a unique name for a’s subset NOTE: set names are arbitrary! We only care that: Find(a) == Find(b) a and b are in the same subset NOTE: outside agent must decide when/what to union; ADT is just the bookkeeper.

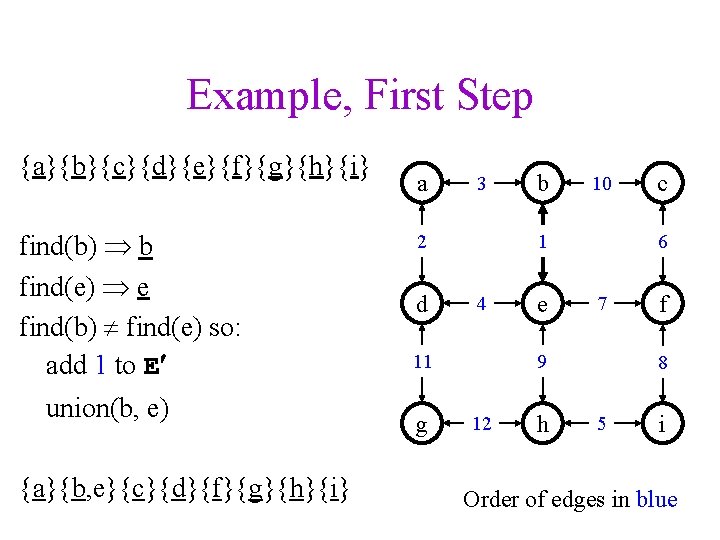
Example a Construct the maze on the right Initial state (set names underlined): {a}{b}{c}{d}{e}{f}{g}{h}{i} 3 2 d g 10 1 4 11 Maze constructor (outside agent) traverses edges in numeric order and decides whether to union b e 6 7 9 12 h c f 8 5 i

Example, First Step {a}{b}{c}{d}{e}{f}{g}{h}{i} find(b) b find(e) e find(b) find(e) so: add 1 to E union(b, e) {a}{b, e}{c}{d}{f}{g}{h}{i} a 3 2 d 10 1 4 11 g b e 6 7 9 12 h c f 8 5 i Order of edges in blue

Up-Tree Intuition Finding the representative member of a set is somewhat like the opposite of finding whether a given item exists in a set. So, instead of using trees with pointers from each node to its children; let’s use trees with a pointer from each node to its parent.

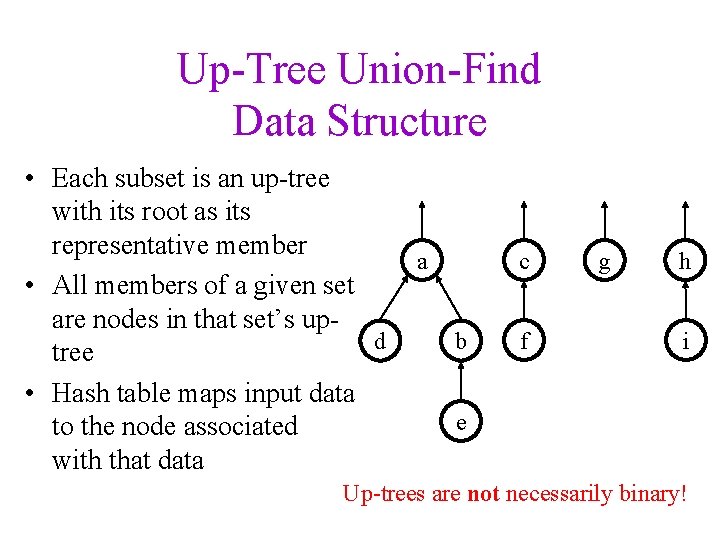
Up-Tree Union-Find Data Structure • Each subset is an up-tree with its root as its representative member • All members of a given set are nodes in that set’s upd tree • Hash table maps input data to the node associated with that data a c b f g h i e Up-trees are not necessarily binary!

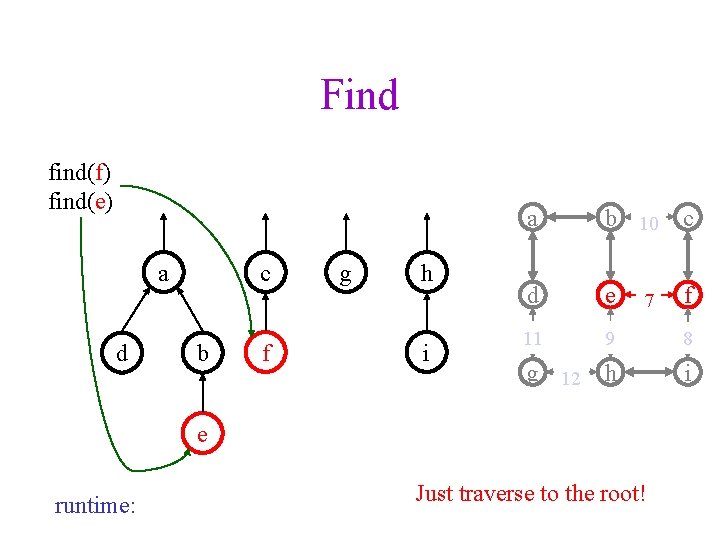
Find find(f) find(e) a d c b f g h i a b 10 c d e 11 9 8 g 12 h i 7 e runtime: Just traverse to the root! f

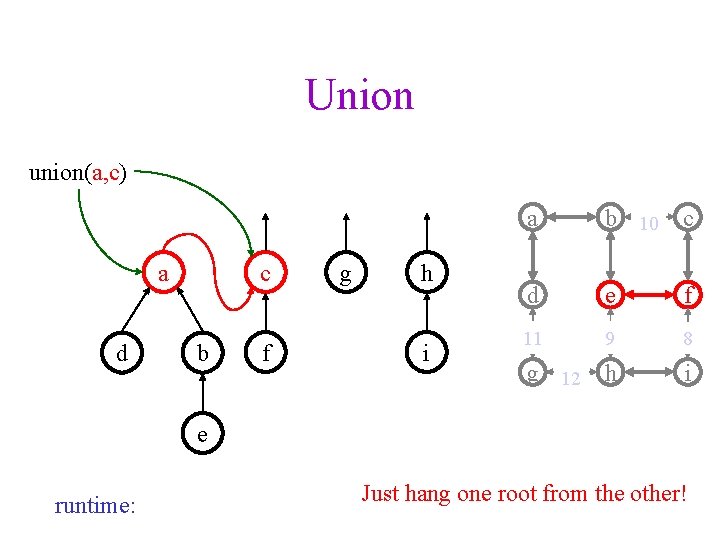
Union union(a, c) a d c b f g h i a b 10 c d e f 11 9 8 g 12 h i e runtime: Just hang one root from the other!

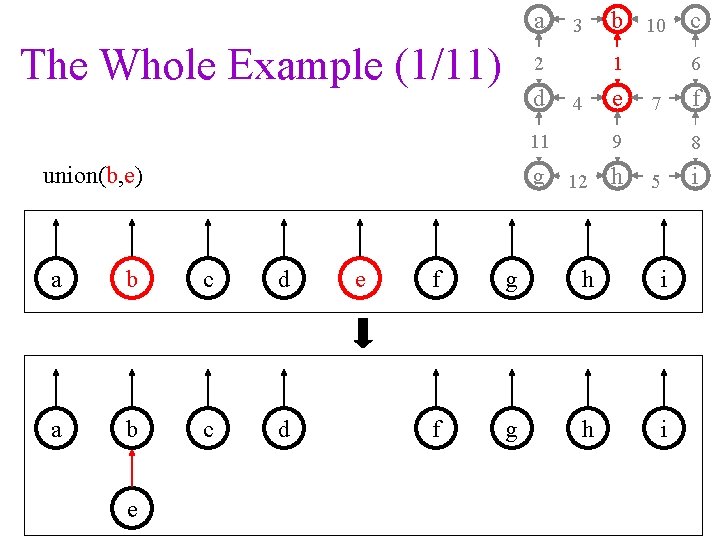
a The Whole Example (1/11) 3 2 d 4 11 union(b, e) c 1 6 e b c d a b c d e 7 9 g 12 h a e b 10 f 8 5 f g h i i

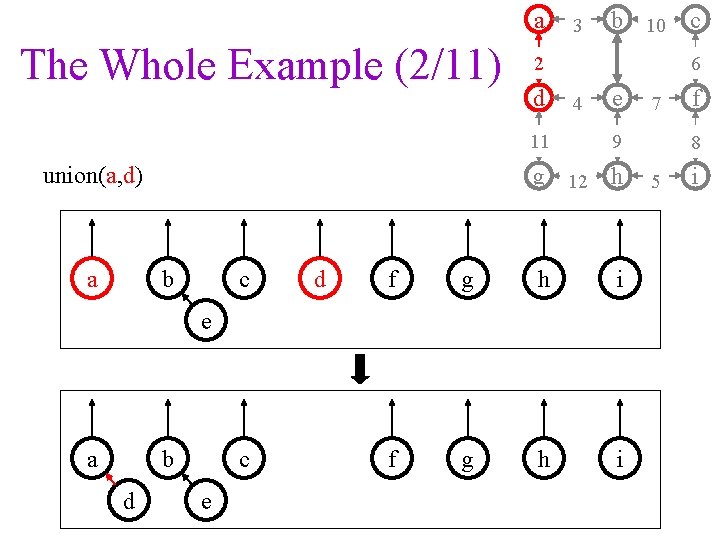
a The Whole Example (2/11) a b 10 2 d 11 union(a, d) 3 6 4 e c d f g h i e a b d c e 7 9 g 12 h b c f 8 5 i

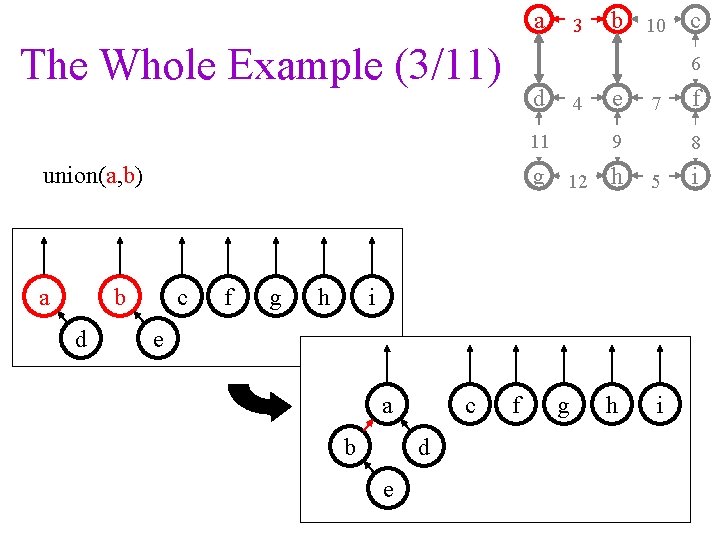
a The Whole Example (3/11) 3 d union(a, b) 4 d e c f g h 7 9 g 12 h b 5 e b c d e f g h f 8 i a c 6 11 a b 10 i i

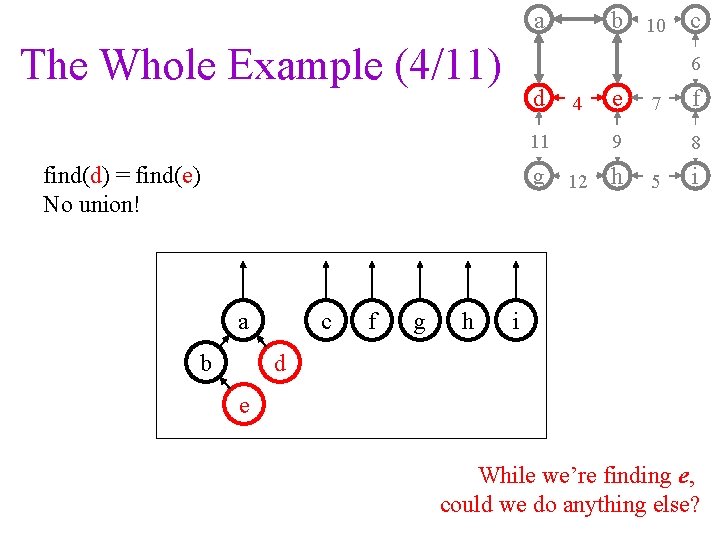
a The Whole Example (4/11) b 10 6 d 11 find(d) = find(e) No union! 4 e b c f g h 7 9 g 12 h a c f 8 5 i i d e While we’re finding e, could we do anything else?

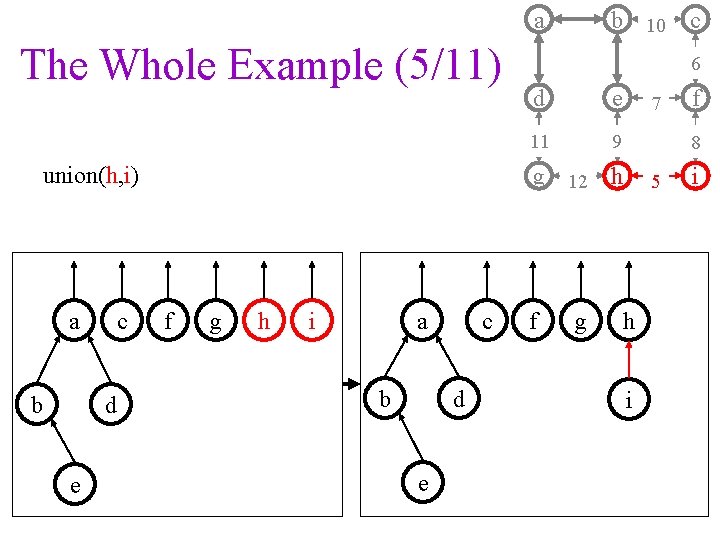
a The Whole Example (5/11) union(h, i) a b c d e b 10 6 d e 11 9 7 g h i a b c d e f g f 8 g 12 h f c 5 h i i

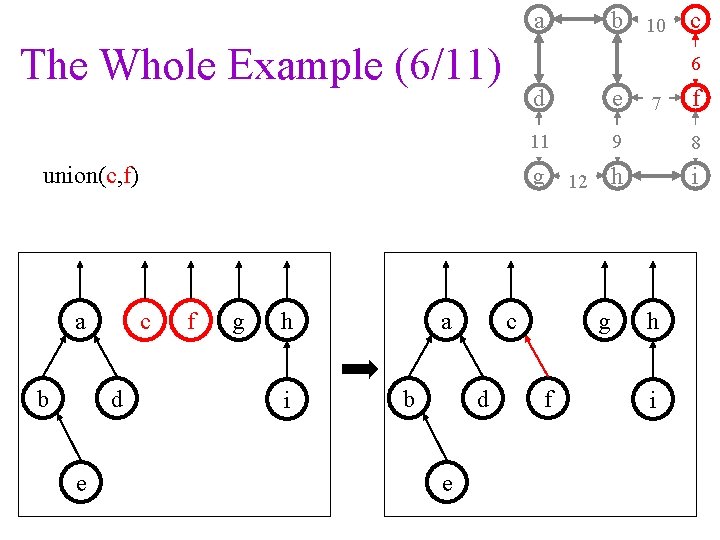
a The Whole Example (6/11) b c d e f g h i a b e d e 11 9 8 g 12 h i c d c 6 union(c, f) a b 10 g f 7 h i f

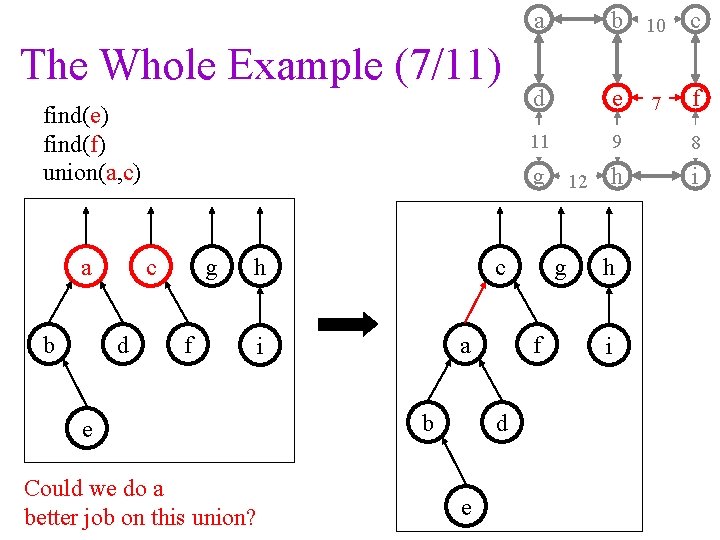
The Whole Example (7/11) find(e) find(f) union(a, c) a b c d g f h Could we do a better job on this union? b 10 c d e f 11 9 8 g 12 h i c a i e a b f d e g h i 7

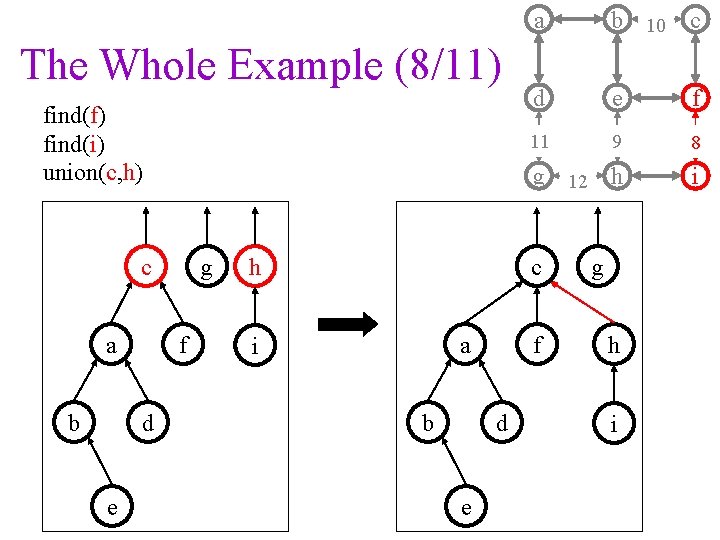
The Whole Example (8/11) find(f) find(i) union(c, h) c a b f d e g h a b 10 c d e f 11 9 8 g 12 h i c a i b f d e g h i

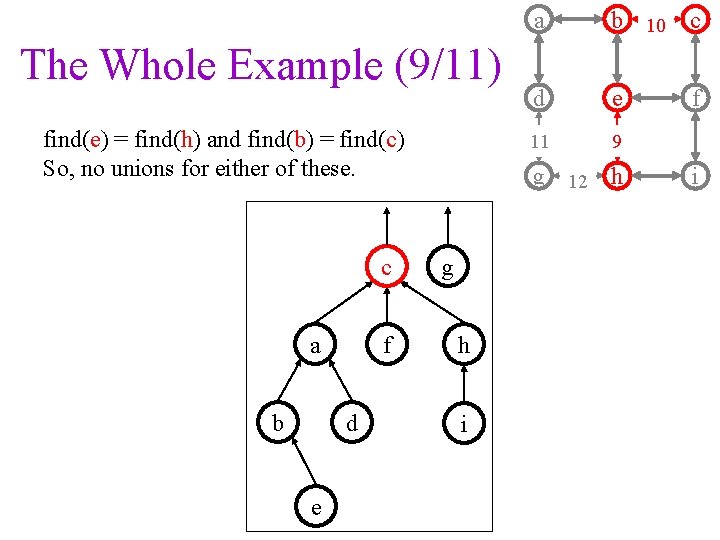
The Whole Example (9/11) find(e) = find(h) and find(b) = find(c) So, no unions for either of these. c a b f d e a b 10 c d e f 11 9 g 12 h g h i i

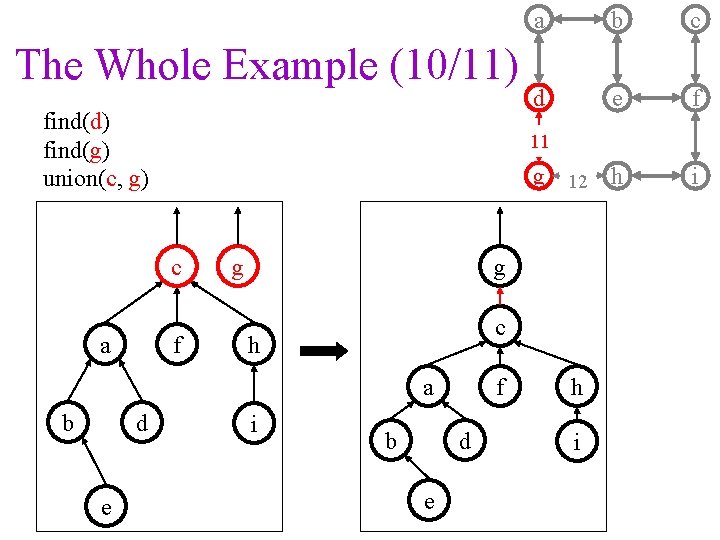
The Whole Example (10/11) find(d) find(g) union(c, g) f g d e c d e f g 12 h i g c h a b b 11 c a a i b f d e h i

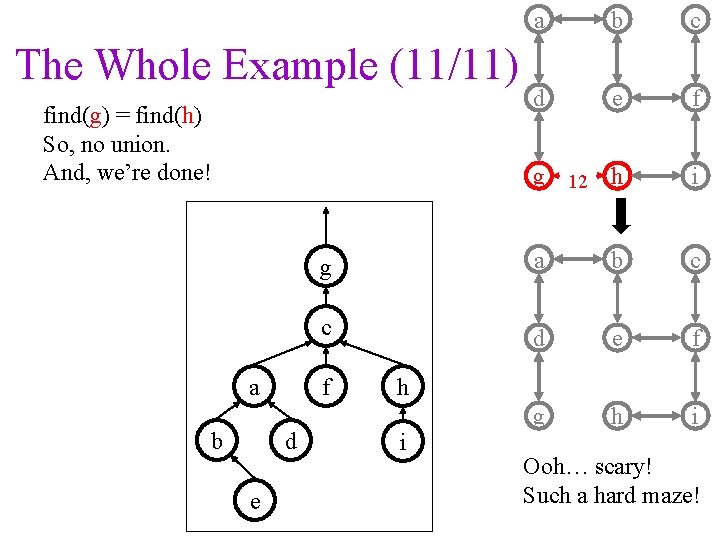
a b c d e f g 12 h i g a b c c d e f g h i The Whole Example (11/11) find(g) = find(h) So, no union. And, we’re done! a b f d e h i Ooh… scary! Such a hard maze!

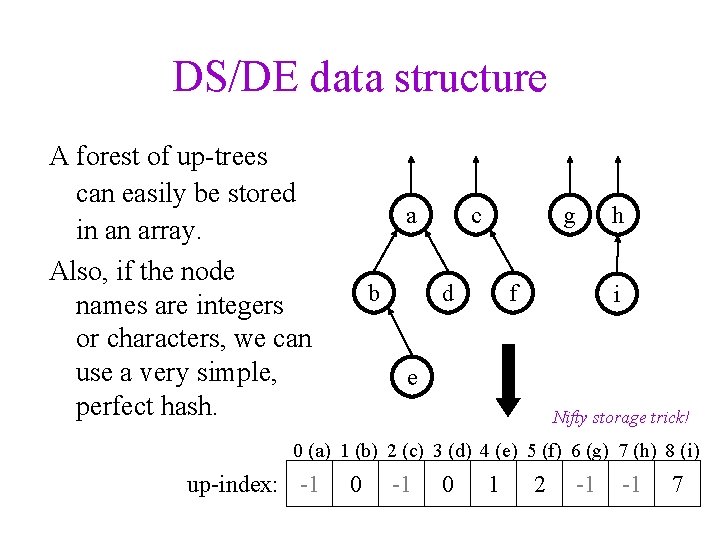
DS/DE data structure A forest of up-trees can easily be stored in an array. Also, if the node names are integers or characters, we can use a very simple, perfect hash. a b c g d f h i e Nifty storage trick! 0 (a) 1 (b) 2 (c) 3 (d) 4 (e) 5 (f) 6 (g) 7 (h) 8 (i) up-index: -1 0 1 2 -1 -1 7

Implementation typedef ID int; ID find(Object x) { assert(h. Table. contains(x)); ID x. ID = h. Table[x]; while(up[x. ID] != -1) { x. ID = up[x. ID]; } ID union(ID x, ID y) { assert(up[x] == -1); assert(up[y] == -1); up[y] = x; } return x. ID; } runtime: O(depth) or … runtime: O(1)

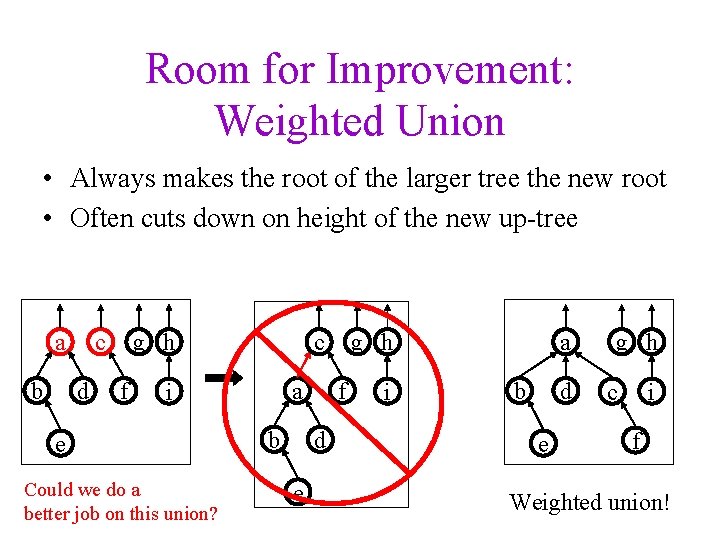
Room for Improvement: Weighted Union • Always makes the root of the larger tree the new root • Often cuts down on height of the new up-tree a b c d g h f c a i e Could we do a better job on this union? b f d e g h i a b d e g h i c f Weighted union!
![Weighted Union Code typedef ID int ID unionID x ID y assertupx Weighted Union Code typedef ID int; ID union(ID x, ID y) { assert(up[x] ==](https://slidetodoc.com/presentation_image_h2/83eb6ad07bc6932fb6a34573967225f3/image-29.jpg)
Weighted Union Code typedef ID int; ID union(ID x, ID y) { assert(up[x] == -1); assert(up[y] == -1); if (weight[x] > weight[y]) { up[y] = x; weight[x] += weight[y]; } else { up[x] = y; weight[y] += weight[x]; } } new runtime of union: new runtime of find:

Weighted Union Find Analysis • Finds with weighted union are O(max up-tree height) • But, an up-tree of height h with weighted union must have at least 2 h nodes Base case: h = 0, tree has 20 = 1 node Induction hypothesis: assume true for h < h • 2 max height n and max height log n • So, find takes O(log n) A merge can only increase tree height by one over the smaller tree. So, a tree of height h -1 was merged with a larger tree to form the new tree. Each tree then has 2 h -1 nodes by the induction hypotheses for a total of at least 2 h nodes. QED.

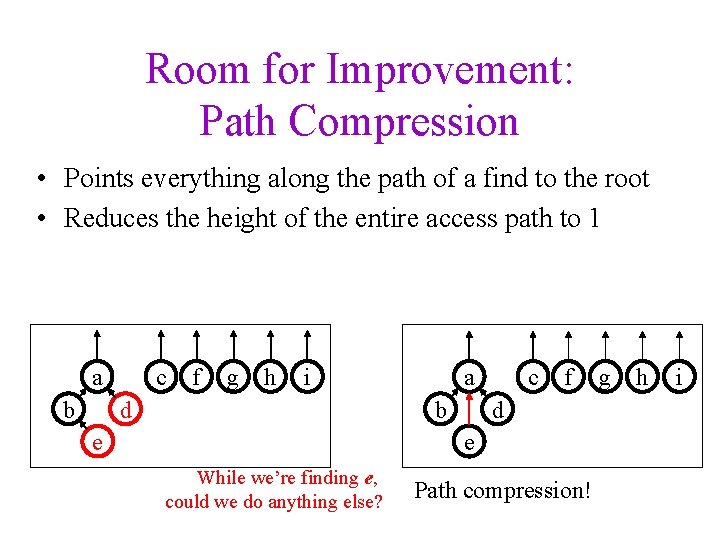
Room for Improvement: Path Compression • Points everything along the path of a find to the root • Reduces the height of the entire access path to 1 a b c f g h i a b d e c f d e While we’re finding e, could we do anything else? Path compression! g h i

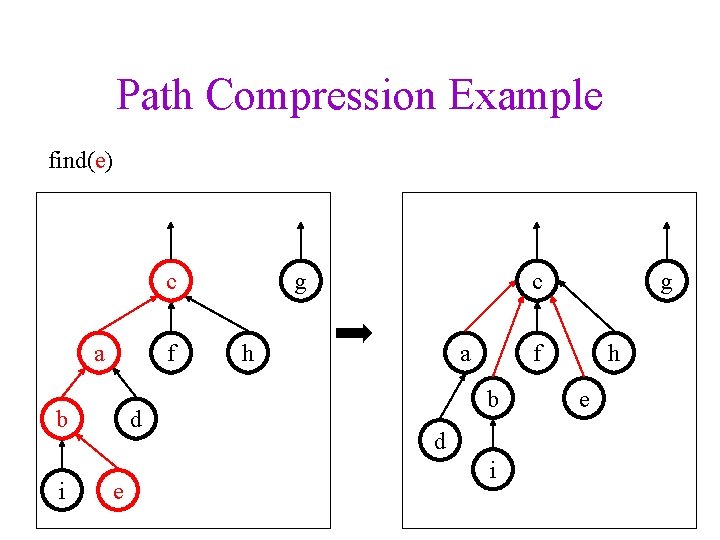
Path Compression Example find(e) c a f b i d e c g h a g f b d i h e

Path Compression Code typedef ID int; ID find(Object x) { assert(h. Table. contains(x)); ID x. ID = h. Table[x]; ID hold = x. ID; while(up[x. ID] != -1) { x. ID = up[x. ID]; } while(up[hold] != -1) { temp = up[hold]; up[hold] = x. ID; hold = temp; } return x. ID; } runtime:

Complexity of Weighted Union + Path Compression Ackermann created a function A(x, y) which grows very fast! Inverse Ackermann function (x, y) grows very slooooowwwly … Single-variable inverse Ackermann function is called log* n How fast does log n grow? log n = 4 for n = 16 Let log(k) n = log (log … (log n))) k logs Then, let log* n = minimum k such that log(k) n 1 How fast does log* n grow? log* n = 4 for n = 65536 log* n = 5 for n = 265536 (20, 000 digit number!) How fast does (x, y) grow? Even sloooowwwer than log* n (x, y) = 4 for n far larger than the number of atoms in the universe (2300)

Complexity of Weighted Union + Path Compression • Tarjan proved that m weighted union and find operations on a set of n elements have worst case complexity O(m (m, n)) • This is essentially amortized constant time • In some practical cases, weighted union or path compression or both are unnecessary because trees do not naturally get very deep.

Disjoint Set Union/Find ADT Summary • Simple ADT, simple data structure, simple code • Complex complexity analysis, but extremely useful result: essentially, constant time! • Lots of potential applications – – Object-property collections Index partitions: e. g. parts inspection To say nothing of maze construction In some applications, it may make sense to have meaningful (non-arbitrary) set names
 Pairwise disjoint vs disjoint
Pairwise disjoint vs disjoint What is a disjoint event
What is a disjoint event Mutually disjoint sets example
Mutually disjoint sets example Mutually disjoint sets example
Mutually disjoint sets example Linked list representation of disjoint sets
Linked list representation of disjoint sets Disjoint set java
Disjoint set java Disjoint sets definition
Disjoint sets definition Cartesian product of sets venn diagram
Cartesian product of sets venn diagram Cse 326
Cse 326 Cse 326
Cse 326 Cse 326
Cse 326 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Homologous structure
Homologous structure Rsg 326-2017-minedu
Rsg 326-2017-minedu Principezinho
Principezinho 4 sinf ona tili 48 mashq
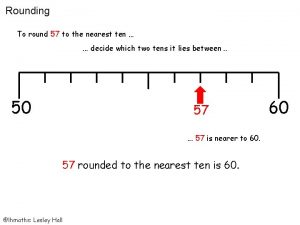
4 sinf ona tili 48 mashq Round 82 to the nearest ten
Round 82 to the nearest ten C#
C# Ssis-326
Ssis-326 Cs326 stanford
Cs326 stanford Cs 326 stanford
Cs 326 stanford Bismarckk
Bismarckk 326 ce
326 ce Decimos centesimos milésimos diezmilésimos
Decimos centesimos milésimos diezmilésimos Cs 326 stanford
Cs 326 stanford Lei 11 326
Lei 11 326 326 os kormányrendelet 2013
326 os kormányrendelet 2013 Ac 326
Ac 326 Manipulating large data sets
Manipulating large data sets Cs 246
Cs 246 Divide data sets in fourths.
Divide data sets in fourths. Paired data sets
Paired data sets Disjoint vs overlapping erd
Disjoint vs overlapping erd Phomosexual
Phomosexual Overlapping events examples
Overlapping events examples Union by rank
Union by rank Els pronoms
Els pronoms