CSE 326 Huffman coding Richard Anderson Code examples

Code examples 000, 001, 010, 011, 100, 101 Coding theory n n n Conversion,

Decode the following E 0 T 11 T 10 N 100 I 1010 I

Prefix code n n No prefix of a A codeword is a B codeword

Prefix codes and binary trees n Tree representation of prefix codes A B C

Construct the tree for the following code E 0 T 11 N 100 I

Minimum length code n n Average cost Average leaf depth Huffman tree – tree

Compute average leaf depth A B C D E 00 0110 0111 1 1/4

Huffman code algorithm n Derivation n Two rarest items will have the longest codewords

Huffman code H = new Heap() for each wi T = new Tree(wi) H.

Example: Weights 4, 5, 6, 7, 11, 14, 21 21 11 4 5 6

Draw a Huffman tree for the following data values and show internal weights: 3,

Correctness proof n n The most amazing induction proof Induction on the number of

Key lemma n Given a tree T, we can find a tree T’, with

Modify the following tree to reduce the WPL 29 10 6 19 4 13

Finish the induction proof n n n n T – Tree constructed by Huffman

X : Any tree, X’: – modified, X’’ : Two smallest leaves removed n

Slides: 17

Download presentation

CSE 326 Huffman coding Richard Anderson

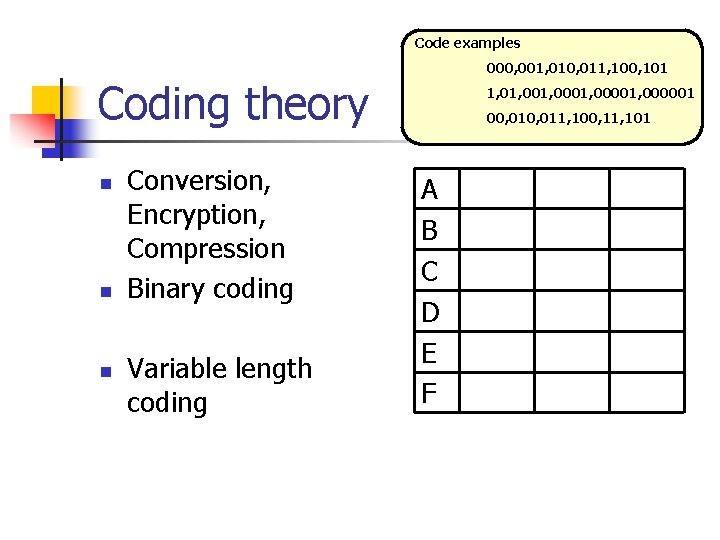
Code examples 000, 001, 010, 011, 100, 101 Coding theory n n n Conversion, Encryption, Compression Binary coding Variable length coding 1, 001, 00001, 000001 00, 011, 100, 11, 101 A B C D E F

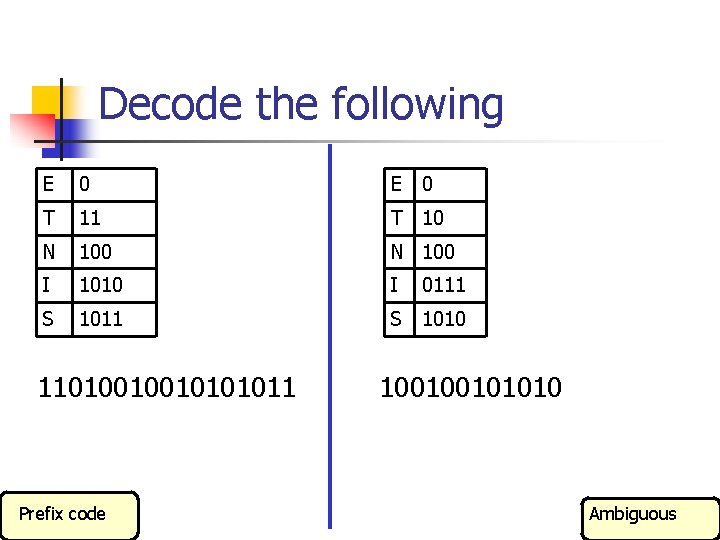
Decode the following E 0 T 11 T 10 N 100 I 1010 I S 1011 S 1010 1101001001011 Prefix code 0111 100100101010 Ambiguous

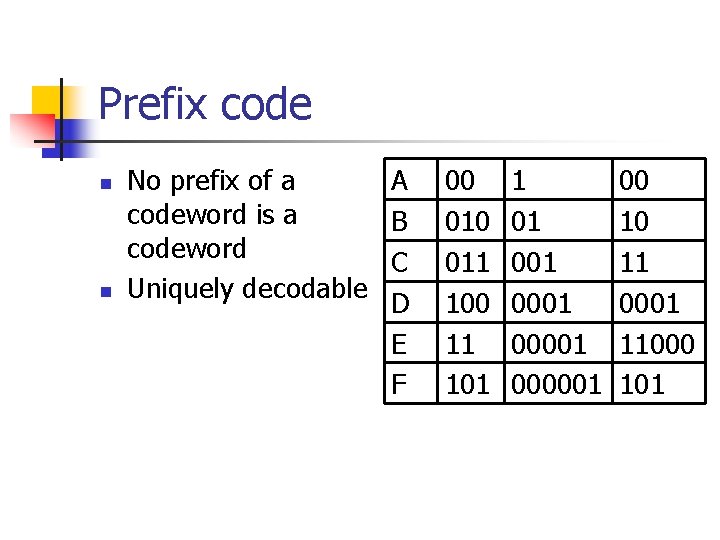
Prefix code n n No prefix of a A codeword is a B codeword C Uniquely decodable D E F 00 011 100 11 101 1 01 0001 000001 00 10 11 0001 11000 101

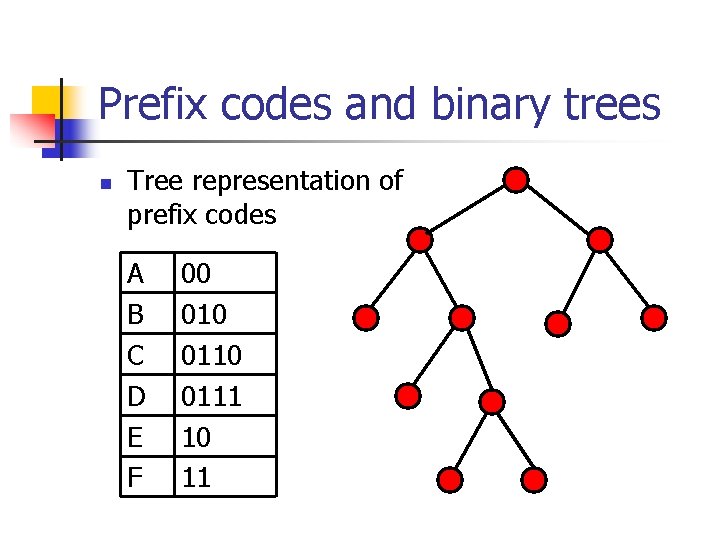
Prefix codes and binary trees n Tree representation of prefix codes A B C D E F 00 0110 0111 10 11

Construct the tree for the following code E 0 T 11 N 100 I 1010 S 1011

Minimum length code n n Average cost Average leaf depth Huffman tree – tree with minimum weighted path length C(T) – weighted path length

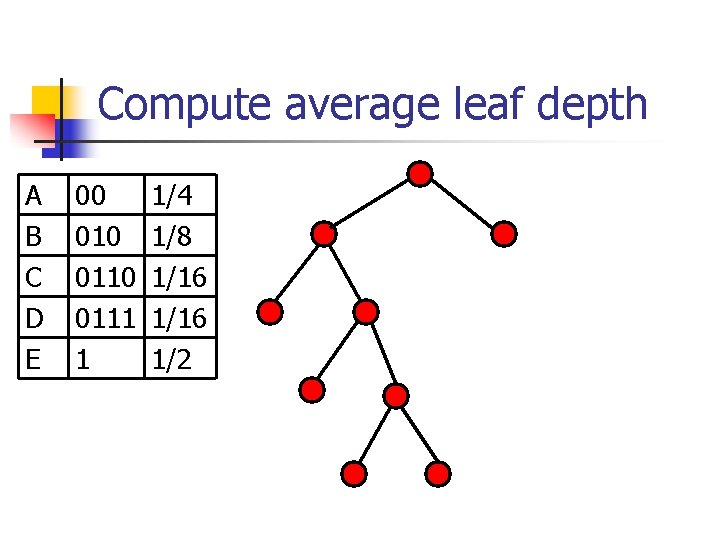
Compute average leaf depth A B C D E 00 0110 0111 1 1/4 1/8 1/16 1/2

Huffman code algorithm n Derivation n Two rarest items will have the longest codewords Codewords for rarest items differ only in the last bit Idea: suppose the weights are with and the smallest weights n n Start with an optimal code for and Extend the codeword for codewords for and to get

Huffman code H = new Heap() for each wi T = new Tree(wi) H. Insert(T) while H. Size() > 1 T 1 = H. Delete. Min() T 2 = H. Delete. Min() T 3 = Merge(T 1, T 2) H. Insert(T 3)

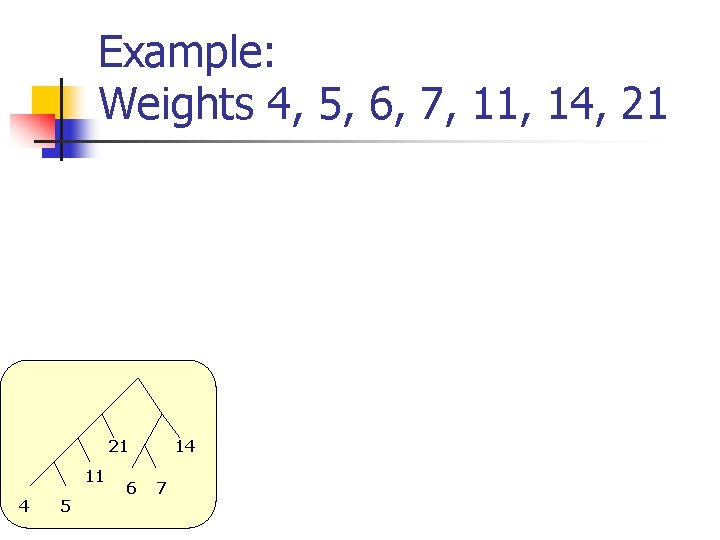
Example: Weights 4, 5, 6, 7, 11, 14, 21 21 11 4 5 6 14 7

Draw a Huffman tree for the following data values and show internal weights: 3, 5, 9, 14, 16, 35

Correctness proof n n The most amazing induction proof Induction on the number of code words The Huffman algorithm finds an optimal code for n = 1 Suppose that the Huffman algorithm finds an optimal code for codes size n, now consider a code of size n + 1. . .

Key lemma n Given a tree T, we can find a tree T’, with the two minimum cost leaves as siblings, and C(T’) <= C(T)

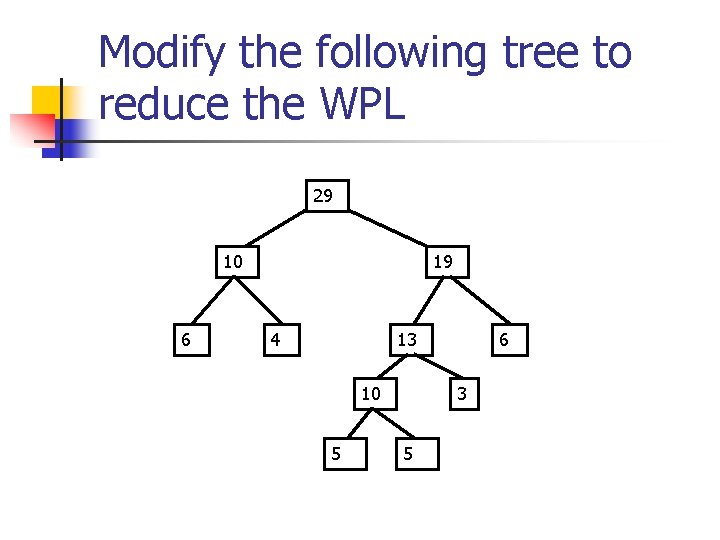
Modify the following tree to reduce the WPL 29 10 6 19 4 13 10 5 6 3 5

Finish the induction proof n n n n T – Tree constructed by Huffman X – Any code tree Show C(T) <= C(X) T’ and X’ – Trees from the lemma C(T’) = C(T) C(X’) <= C(X) T’’ and X’’ – Trees with minimum cost leaves x and y removed

X : Any tree, X’: – modified, X’’ : Two smallest leaves removed n n C(X’’) = C(X’) – x – y C(T’’) = C(T’) – x – y C(T’’) <= C(X’’) C(T) = C(T’’) + x + y <= C(X’’) + x + y = C(X’) <= C(X)