Probabilities of Disjoint and Overlapping Events Standards from

Probabilities of Disjoint and Overlapping Events Standard(s) from Instructional Guide: SDAP 3. 2 Use data to estimate the probability of future events (e. g. , batting averages or number of accidents per mile driven Student Objective (s): - Students will use data to estimate the probability of disjoint and overlapping future events by solving problems independently and demonstrating proficiency with 80% accuracy

Definitions: l Disjoint events – (mutually exclusive events) are events that have no outcomes in common. l Overlapping events – are events that have one or more outcomes in common.

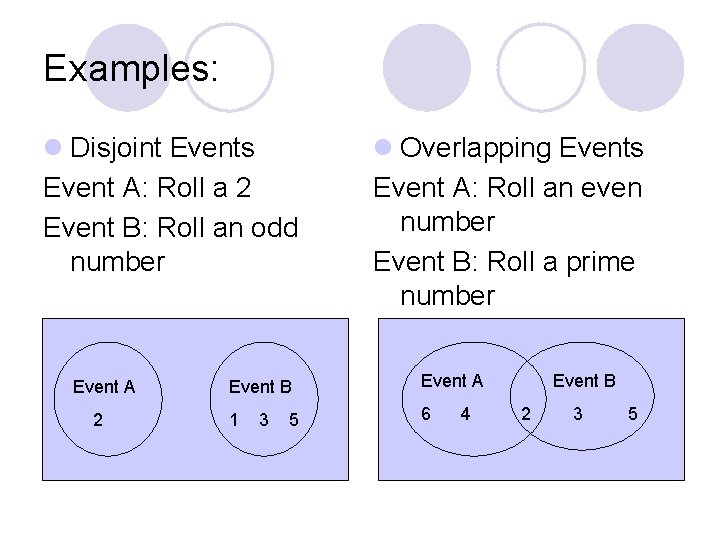
Examples: l Disjoint Events Event A: Roll a 2 Event B: Roll an odd number l Overlapping Events Event A: Roll an even number Event B: Roll a prime number Event A Event B 2 1 3 5 6 4 2 3 5

Tell whether the events are disjoint or overlapping. (Hint draw Venn diagram) l Roll a number cube. l Randomly select a student. Event A: Roll a number less than 4 Event A: Select an 8 th grader. Event B: Roll a 5 Event B: Select a boy

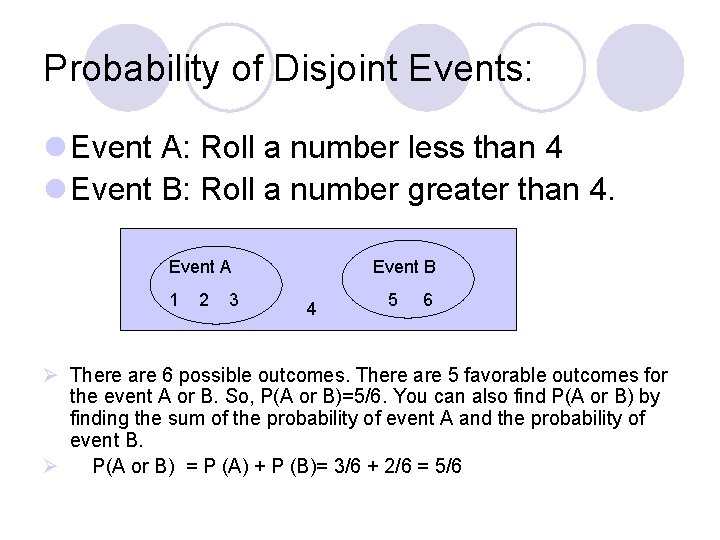
Probability of Disjoint Events: l Event A: Roll a number less than 4 l Event B: Roll a number greater than 4. Event A 1 2 3 Event B 4 5 6 Ø There are 6 possible outcomes. There are 5 favorable outcomes for the event A or B. So, P(A or B)=5/6. You can also find P(A or B) by finding the sum of the probability of event A and the probability of event B. Ø P(A or B) = P (A) + P (B)= 3/6 + 2/6 = 5/6

Sooooo: l If A and B are disjoint events, P(A or B) = P (A) + P (B)

Practice Finding the Probability of Disjoint Events: l Fifty tickets are sold for a raffle. You buy 2 tickets, and your friend buys 3 tickets. One ticket is randomly chosen as the winning ticket. What is the probability that you or your friend wins the raffle? l The events are disjoint b/c you and your friend can not both win. Ø Event A: You win Ø Event B: Your friend wins Ø P( A or B) = P (A) + P (B) 2/50 + 3/50 = 5/50 = 1/10

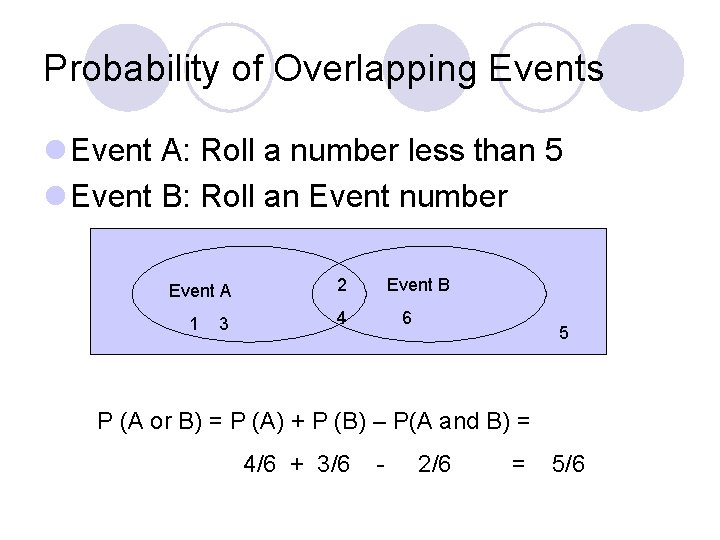
Probability of Overlapping Events l Event A: Roll a number less than 5 l Event B: Roll an Event number Event A 2 Event B 1 3 4 6 5 P (A or B) = P (A) + P (B) – P(A and B) = 4/6 + 3/6 - 2/6 = 5/6