Chapter 4 Lexical and Syntax Analysis ISBN 0

Chapter 4 Lexical and Syntax Analysis ISBN 0 -321 -33025 -0

Chapter 4 Topics • • • Introduction Lexical Analysis The Parsing Problem Recursive-Descent Parsing

Why study lexical and syntax analyzers? • Shows application of grammars discussed in chapter 3 • Lexical and syntax analysis not just used in compiler design: – program listing formatters – programs that compute complexity – programs that analyze and react to configuration files • Good to have some background, since compiler design not required Copyright © 2006 Addison-Wesley. All rights reserved. 1 -3

Unsolicited email from student… Hiyo, For my internship (and hopefully soon full-time job) one of the projects I'm doing is managing all of the config files for all the servers and devices we have. They're generated from templates, and then manual updates are also added, and we want to keep track of all the data, and make sure all of those configs are up to date and correct, mirror what we think it should be in the database, and a few other things to end a lot of late-night headaches. A lot of the aspects of this have me going over notes again from Programming Languages, in dealing with understanding syntax, parsing, etc. Thought you might enjoy seeing those lessons being applied in the "real world"! Copyright © 2006 Addison-Wesley. All rights reserved.

Introduction • Language implementation systems must analyze source code, regardless of the specific implementation approach (compiled, interpreted, hybrid) • Nearly all syntax analysis is based on a formal description of the syntax of the source language (context-free grammars or BNF) • The parser can be based directly on the BNF • Parsers based on BNF are easy to maintain (modular) Copyright © 2006 Addison-Wesley. All rights reserved. 1 -5

Syntax Analysis • The syntax analysis portion of a language processor nearly always consists of two parts: – A low-level part called a lexical analyzer (mathematically, a finite automaton based on a regular grammar). Also called a scanner. – A high-level part called a syntax analyzer, or parser (mathematically, a push-down automaton based on a context-free grammar, or BNF) Copyright © 2006 Addison-Wesley. All rights reserved. 1 -6

Reasons to Separate Lexical and Syntax Analysis • Simplicity - less complex approaches can be used for lexical analysis; separating them simplifies the parser • Efficiency - separation allows optimization of the lexical analyzer – lex is fast! • Portability - parts of the lexical analyzer may not be portable, but the parser always is portable Why? Copyright © 2006 Addison-Wesley. All rights reserved. 1 -7

Lexical Analysis • A lexical analyzer is a pattern matcher for character strings • A lexical analyzer is a “front-end” for the parser. Views source as single string of characters. • Identifies substrings of the source program that belong together - lexemes – Lexemes match a character pattern, which is associated with a lexical category called a token, normally represented as an enum/int – sum is a lexeme; its token may be IDENT Copyright © 2006 Addison-Wesley. All rights reserved. 1 -8

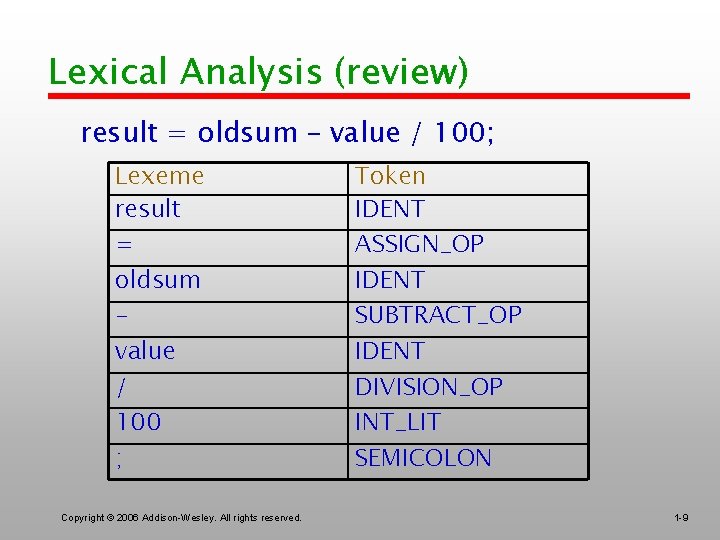
Lexical Analysis (review) result = oldsum – value / 100; Lexeme result = oldsum value / 100 ; Copyright © 2006 Addison-Wesley. All rights reserved. Token IDENT ASSIGN_OP IDENT SUBTRACT_OP IDENT DIVISION_OP INT_LIT SEMICOLON 1 -9

Lexical Analysis (continued) • The lexical analyzer is usually a function that is called by the parser when it needs the next token (used to process entire file at one time) • Skips comments and whitespace • May insert lexemes for user-defined names into symbol table • Detects syntax errors in tokens, such as ill-formed floating point literals oldsum = subtract_op assign_op ident result = oldsum – value / 100; Copyright © 2006 Addison-Wesley. All rights reserved. Scanner value ident … 1 -10

Lexical Analysis (continued) Three approaches to building a lexical analyzer: • Write a formal description of the tokens based on regular expressions and use a software tool that constructs a lexical analyzer given such a description (e. g. , lex, flex) • Design a state diagram that describes the tokens and write a program that implements the state diagram • Design a state diagram that describes the tokens and hand-construct a table-driven implementation of the state diagram Copyright © 2006 Addison-Wesley. All rights reserved. 1 -11

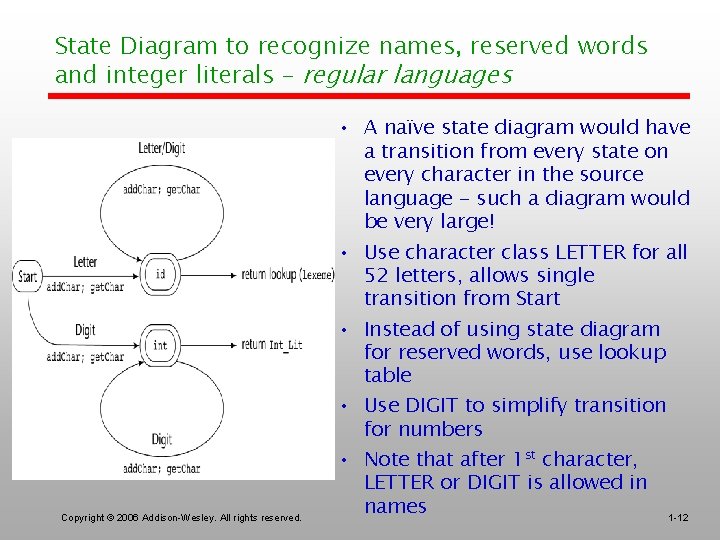
State Diagram to recognize names, reserved words and integer literals – regular languages Copyright © 2006 Addison-Wesley. All rights reserved. • A naïve state diagram would have a transition from every state on every character in the source language - such a diagram would be very large! • Use character class LETTER for all 52 letters, allows single transition from Start • Instead of using state diagram for reserved words, use lookup table • Use DIGIT to simplify transition for numbers • Note that after 1 st character, LETTER or DIGIT is allowed in names 1 -12

Lexical Analysis (cont. ) Implementation (assume initialization): int lex() { get. Char(); // puts char in next. Char, type in char. Class // skips white space switch (char. Class) { case LETTER: // Notice correspondence to state transition add. Char(); // appends next. Char onto lexeme get. Char(); while (char. Class == LETTER || char. Class == DIGIT) { add. Char(); get. Char(); } return lookup(lexeme); break; … Copyright © 2006 Addison-Wesley. All rights reserved. 1 -13

Lexical Analysis (cont. ) … so this corresponds to… case DIGIT: add. Char(); get. Char(); while (char. Class == DIGIT) { add. Char(); get. Char(); How would 123 abc } interpreted? return INT_LIT; break; } /* End of switch */ } /* End of function lex */ Copyright © 2006 Addison-Wesley. All rights reserved. be 1 -14

Compiler Tools • Now is a good time to look at lex/flex Copyright ©

The Parsing Problem (syntax analysis) • Goals of the parser, given an input program: – Find all syntax errors; for each, produce an appropriate diagnostic message, and recover quickly (to check rest of program) – Produce the parse tree, or at least a trace of the parse tree, for the program. The parse tree is used as the basis for translation. – Parse tree contains all the information needed by a language processor Copyright © 2006 Addison-Wesley. All rights reserved. 1 -16

The Parsing Problem (cont. ) • Two categories of parsers – Top down - produce the parse tree, beginning at the root • Order is that of a leftmost derivation • Traces or builds the parse tree in preorder – Bottom up - produce the parse tree, beginning at the leaves • Order is that of the reverse of a rightmost derivation • Parsers look only one token ahead in the input Copyright © 2006 Addison-Wesley. All rights reserved. 1 -17

Which will we study? • Both! • First we’ll look at top-down techniques (recursive descent parsing) and problems with left-recursive grammars. We’ll code a basic recursive descent parser. • Then we’ll look at bottom-up parsing and how to use yacc/bison Copyright © 2006 Addison-Wesley. All rights reserved.

The Parsing Problem: Top-Down Non-terminal string of terminals • Consider the sentential form x. A mixed string • Top-down Parsers – parser must choose the correct rule for nonterminal A to get the next sentential form in the leftmost derivation, using only the first token produced by A Notational conventions: • Terminal symbols – lowercase letters at beginning of alphabet (a, b, . . . ) • Nonterminal symbols – uppercase letters at beginning of alphabet (A, B, . . . ) • Terminals or nonterminals – uppercase letters at end of alphabet (W, X, Y, Z) • Strings of terminals – lowercase letters at end of alphabet (w, x, y, z) • Mixed strings (terminals and/or nonterminals) – lowercase Greek letters ( ) • Example: a = <term> + <expr> Copyright © 2006 Addison-Wesley. All rights reserved. 1 -19

Top-Down Parsing, continued • Parsing x. A • Assume three A-rules are: A->b. B | c. Bb |a Next sentential form could be xb. B , xc. Bb or xa • Compare next token of input with first symbol generated by each rule. Not always easy, could be a nonterminal. May need to backtrack. What does that mean? Copyright © 2006 Addison-Wesley. All rights reserved.

Backtrack Example • Parsing ba • Assume the rules are (start symbol is A):

The Complexity of Parsing • Parsers that work for any unambiguous grammar are complex and inefficient ( O(n 3), where n is the length of the input ). Algorithms must frequently back up and reparse, requires more maintenance of tree. Too slow to be used in practice. • Compilers use parsers that only work for a subset of all unambiguous grammars, but do it in linear time ( O(n), where n is the length of the input ) Copyright © 2006 Addison-Wesley. All rights reserved. 1 -22

Types of Top-Down Parsers The most common top-down parsing algorithms: – Recursive descent - a coded implementation – LL parsers - table driven implementation • L left-to-right scan, L leftmost derivation (LL) ANTLR is an LL(*) recursive-descent parser generator LL(*) means not restricted to a finite k tokens of lookahead Copyright © 2006 Addison-Wesley. All rights reserved. 1 -23

Recursive-Descent Parsing • Hand-coded solution – general approach • Write a subprogram for each nonterminal (e. g. , <expr>) • Subprograms may be recursive (e. g. , for nested structures) • Collect all subprograms • Produces a parse tree in top-down order • EBNF is ideally suited to be the basis for a recursive -descent parser, because EBNF minimizes the number of nonterminals (i. e. , fewer subprograms) Copyright © 2006 Addison-Wesley. All rights reserved. 1 -24

Recursive-Descent Parsing (cont. ) • A grammar for simple expressions: <expr> <term> {(+ | -) <term>} <term> <factor> {(* | /) <factor>} <factor> id | ( <expr> ) • A grammar for selection and declaration <if-statement> if <logic_expr><statement>[else <statement>] <ident-list> ident {, <ident>} • Grammar does not enforce associativity rules, compiler must Copyright © 2006 Addison-Wesley. All rights reserved. 1 -25

Recursive-Descent Parsing (cont. ) • Assume we have a lexical analyzer function named lex, which puts the next token code in next. Token • Simple case: only one RHS for a nonterminal – For each terminal symbol in the RHS (e. g. , if), compare it with the next input token; if they match, continue, else there is an error – For each nonterminal symbol in the RHS (e. g. , <term>), call its associated parsing subprogram Example to follow… Copyright © 2006 Addison-Wesley. All rights reserved. 1 -26

Recursive-Descent Parsing (cont. ) /* Function expr Parses strings in the language generated by the rule: <expr> → <term> {(+ | -) <term>} */ void expr() { // Parse the first term(); /* As long as the next token is + or -, call lex to get the next token, and parse the next term */ while (next. Token == PLUS_CODE || next. Token == MINUS_CODE){ lex(); // get next token term(); This particular routine does not detect errors } } Convention: Every parsing routine leaves the next token in next. Token Copyright © 2006 Addison-Wesley. All rights reserved. 1 -27

Recursive-Descent Parsing (cont. ) • More complex: Nonterminal has more than one RHS. Requires an initial process to determine which RHS it is to parse. – The correct RHS is chosen on the basis of the next token of input (the lookahead) – The next token is compared with the first token that can be generated by each RHS until a match is found – If no match is found, it is a syntax error Copyright © 2006 Addison-Wesley. All rights reserved. 1 -28

Recursive-Descent Parsing (cont. ) /* Function factor Parses strings in the language generated by the rule: <factor> -> id | ( <expr> ) */ void factor() { // Determine which RHS if (next. Token) == ID_CODE) lex(); // For the RHS id, just call lex /* If the RHS is ( <expr> ) – call lex to pass over the left parenthesis, call expr, then check for the right parenthesis */ else if (next. Token == LEFT_PAREN_CODE) { lex(); // skip over ( expr(); // ensure we have an expression if (next. Token == RIGHT_PAREN_CODE) lex(); // ensure the next is a ) else error(); } /* End of else if (next. Token ==. . . */ else error(); /* Neither RHS matches */ } Copyright © 2006 Addison-Wesley. All rights reserved. 1 -29

Recursive-Descent Parsing (cont. ) /* Function term Parses strings in the language generated by the rule: <term> -> <factor> {(* | /) <factor>} */ void term() { /* Parse the first factor */ factor(); /* Keep processing term as long as * or / */ while (next. Token == AST_CODE || next. Token == SLASH_CODE) { lex(); // just skip over * and / factor(); } } Copyright © 2006 Addison-Wesley. All rights reserved. 1 -30

Recursive-Descent Parsing (cont. ) • Trace the code for a + b – – – Call lex // sets next. Token to a, ID_CODE Enter <expr> Enter <term> Enter <factor> // a is factor Call lex // sets next. Token to +, PLUS_CODE Exit <factor> Exit <term> // only 1 factor, no * or / + matches PLUS_CODE // while loop Call lex // sets next. Token to b, ID_CODE Enter <term> Enter <factor> // b is factor Call lex // sets next. Token to end-of-input Exit <factor> Exit <term> Exit <expr> //end while Copyright © 2006 Addison-Wesley. All rights reserved. 1 -31

Recursive-Descent Parsing (cont. ) • Parse tree for a + b <expr> <term> <factor>

Recursive Descent Quick Exercise • Do Recursive Descent exercises 1 Copyright © 2006 Addison-Wesley.

Recursive-Descent Parsing / LL Grammars and Left Recursion • Important to consider limitations of recursivedescent in terms of grammar restrictions Left-to-right scan Leftmost • The LL Grammar Class – The Left Recursion Problem • If a grammar has left recursion, either direct or indirect, it cannot be the basis for a top-down parser • A grammar can be modified to remove left recursion – A -> A + B // direct left recursive – continues to try to parse A Copyright © 2006 Addison-Wesley. All rights reserved. 1 -34

Left Recursion Example E -> E + T | T T -> T * F | F F -> (E) | id x + y + z next. Token = x E // terminal symbol not matched E + T + T // terminal symbol not matched A person, of course, would choose T rather than E + T, but the function for <expr> is deterministic, would always choose E + T Copyright © 2006 Addison-Wesley. All rights reserved. 1 -35

Left Recursion– How to remove? A -> A | A A • Left-recursive string A A->A -> A. . . A -> A’ A R A’ -> A’ | R R. . . • Right-recursive string R A-> A’-> A’ . . . -> Both strings are followed by series of s Copyright © 2006 Addison-Wesley. All rights reserved. 1 -36

Convince yourself (quick exercise) Grammar with Left recursion A -> Ax | -> z Grammar without left recursion A -> A’ A’ -> x. A’ | We could just do x for this simple grammar, but see next slide -> z Which grammar (or both) can produce: • zxxx Copyright © 2006 Addison-Wesley. All rights reserved.

Slightly more complex example Grammar with Left recursion A -> Ax | Ay | Az | -> c Grammar without left recursion A -> A’ A’ -> x. A’ | y. A’ | z. A’ | -> c Grammar without left recursion or erasure rule, suggested by a student: A -> A’ A’ -> x. A’ | y. A’ | z. A’ | x | y | z -> c Are these equivalent? Can we parse c?

LL Grammars/Removing Left Recursion • To remove direct left recursion: – For each nonterminal, A, 1. Group the A-rules as: recursive rules A->A 1, |. . . |A m| 1|. . . | n where none of the s begin with A 2. Replace the original A-rules with A -> 1 A' | 2 A' |. . . + n. A' A' -> 1 A' |. . . m. A' | erasure rule where is the empty string NOTE: The effect of original A rules is to add s to end of string, the revised rules add s to the end of the string, then get rid of the A Copyright © 2006 Addison-Wesley. All rights reserved. 1 -39

Recursive-Descent Parsing / LL Grammars (cont) E -> E + T | T T -> T * F | F F -> (E) | id • E-Rules Think of T as base case 1 = + T and = T – E -> T E' Remember: A -> A' – E' -> + T E' | Remember: A' -> A' • T-Rules – 1 = * F and = F – T -> F T' – T' -> * F T' | 1 Copyright © 2006 Addison-Wesley. All rights reserved. Revised Grammar E -> T E' E' -> + T E' | T -> F T' T' -> * F T' | F -> (E) | id 1 -40

Recursive-Descent Parsing / LL Grammars (cont) – Grammar generates the same language but is not left recursive. Ex: A + B * C • T E' //rule 1 1. 2. 3. 4. 5. • F T ' E ' // rule 3 E -> T E' • A T’ E' // rule 5 E' -> + T E' | • F E ' // rule 4 erasure T -> F T' • A + T E' // rule 2 T' -> * F T' | • A + F T' E’ // rule 3 F -> (E) | id • A + B T' E’ // rule 5 • A + B * F T' E’// rule 4 • A + B * C T' E’// rule 5 • A + B * C E’ // erasure rule • A + B * C // erasure rule Copyright © 2006 Addison-Wesley. All rights reserved. E -> E + T | T T -> T * F | F F -> (E) | id – – – – E+T T+T F+T A+T*F A+F*F A+B*C 1 -41

What about EBNF? E -> E + T | T T -> T * F | F F -> (E) | id Could be: E -> T { + T} T -> F { * F} F -> (E) | id Translates to while loop in recursive descent

More complex example The general solution using BNF may be easier to deal with for more complex rules: E -> E + T | E ** F T -> T * F | F F -> (E) | id NOTE: The above grammar would not have correct precedence, the purpose is just to show that it might not always be so easy to convert left recursion to EBNF. When it can be done easily, converting to EBNF would be a good approach. E -> TE’ E’->+TE’ | **FE’ | T -> F T' T' -> * F T' | F -> (E) | id

Recursive-Descent Parsing / LL Grammars (cont) • Indirect left recursion poses same problem A -> B a A B -> A b • A subprogram calls B, which calls A • Algorithm to remove indirect left recursion not in text • This is a problem for all top-down parsing algorithms, not just recursive descent • Good news: When writing a grammar for a programming language, can usually avoid left recursion (both types) Copyright © 2006 Addison-Wesley. All rights reserved. 1 -45

Left Recursion Exercise Consider the simple grammar: CSM -> CSM a | ORE -> g Show that this grammar can generate gaa. Rewrite the grammar to remove the left recursion. Show that it can still generate gaa. Copyright © 2006 Addison-Wesley. All rights reserved.

Recursive-Descent Parsing /LL Grammars & pairwise disjointness • Need to be able to choose RHS on the basis of the next token, using only first token generated by leftmost nonterminal • Test to determine whether this can be done is pairwise disjointness test. • Must compute a set named FIRST based on RHSs of nonterminal symbol Copyright © 2006 Addison-Wesley. All rights reserved. 1 -47

Recursive-Descent Parsing /LL Grammars & pairwise disjointness • Pairwise Disjointness Test: – For each nonterminal, A, in the grammar that has more than one RHS, for each pair of rules, A i and A j, it must be true that FIRST( i) FIRST( j) = • Examples: A a. B | b. Ab | Bb B -> c. B | d – FIRST of A-rules are {a}, {b} and {c, d} These are disjoint – FIRST of B-rules are {c}, {d} Also disjoint – NOTE that we do the FIRST of all non-terminals, not just the first one Copyright © 2006 Addison-Wesley. All rights reserved. 1 -48

Recursive-Descent Parsing /LL Grammars & pairwise disjointness A -> a. B | Bab B -> a. B | g – FIRST sets of A are {a} and {a, g} which are NOT disjoint – If next input is an a, can't decide which RHS – Becomes more complex as more RHSs begin with nonterminals • Example: do top-down parse of ag using just a one-token lookahead. – token is a. Do I apply a. B or Bab? – remember recursive descent coding: • if (next. Token == ‘a’) // do what? ? Copyright © 2006 Addison-Wesley. All rights reserved. 1 -49

Pairwise Disjoint cautions • Simple Pairwise Disjoint A -> a. B | a. C // FIRST(A) = {a}, {a} not disjoint B -> x // FIRST(B) = {x} C-> y // FIRST(C ) = {y} • Is this pairwise disjoint? A -> a. B | g. C B -> x is this a problem? C -> x • left Recursive is not the same as Pairwise disjoint A -> Aa | a. B B -> x Copyright © 2006 Addison-Wesley. All rights reserved.

Recursive-Descent Parsing (cont. ) • Left factoring can sometimes resolve the problem Replace <variable> identifier | identifier [<expression>] with <variable> identifier <idarg> | [<expression>] or <variable> identifier [[<expression>]] (the outer brackets are metasymbols of EBNF indicating that inside is optional) Copyright © 2006 Addison-Wesley. All rights reserved. 1 -52

Pairwise Disjoint Exercise • Do the Pairwise Disjoint Exercise Copyright © 2006 Addison-Wesley. All

Bottom-Up Parsing – the Idea • Example grammar and derivation: S -> a. Ac A -> a. A | b grammar S => a. Ac => aabc sample derivation • Starting with sentence, aabc, must find handle. • String aabc contains RHS b. Yields aa. Ac. • String aa. Ac contains handle a. A. Yields a. Ac. • String a. Ac contains handle a. Ac. Yields S. Copyright © 2006 Addison-Wesley. All rights reserved. 1 -54

The Parsing Problem: Bottom-Up • Bottom-up parsers – Given a right sentential form, , determine what substring of is the RHS of the rule in the grammar that must be reduced to produce the previous sentential form in the right derivation – Given sentential form may include more than one RHS from the language grammar – The correct RHS is called the handle. – The most common bottom-up parsing algorithms are in the LR family (Left-to-right scan, generates Rightmost derivation) Copyright © 2006 Addison-Wesley. All rights reserved. 1 -55

Quick Exercise Given the grammar: Goal -> a. ABe A -> Abc | b B -> d and the input string abbcde: Do a bottom-up parse to determine whether the string is a sentence in the language. Example from Engineering a Compiler Copyright © 2006 Addison-Wesley. All rights reserved.

Bottom-up Parsing • Bottom-up parser starts with last sentential form (input sentence – no non-terminals) and produces sequence of forms until all that remains is the start symbol • The parsing problem is finding the correct RHS (handle) in a right-sentential form to reduce to get the previous right-sentential form in the derivation • Grammars can be left recursive • Grammars do not generally include metasymbols used in EBNF Copyright © 2006 Addison-Wesley. All rights reserved. 1 -57

Bottom-up Parsing Simple Example Compare the derivation/parse using the same grammar Sample derivation* Sample bottom-up parse left recursion E -> E + T | T T -> T * F | F F -> (E) | id E =>E + T => E + T * F => E + T * id => E + F * id => E + id * id => T + id * id =>F + id * id => id + id * id => F + id * id => T + id * id => E + F * id => E + T * F => E + T => E *rightmost Copyright © 2006 Addison-Wesley. All rights reserved. 1 -58

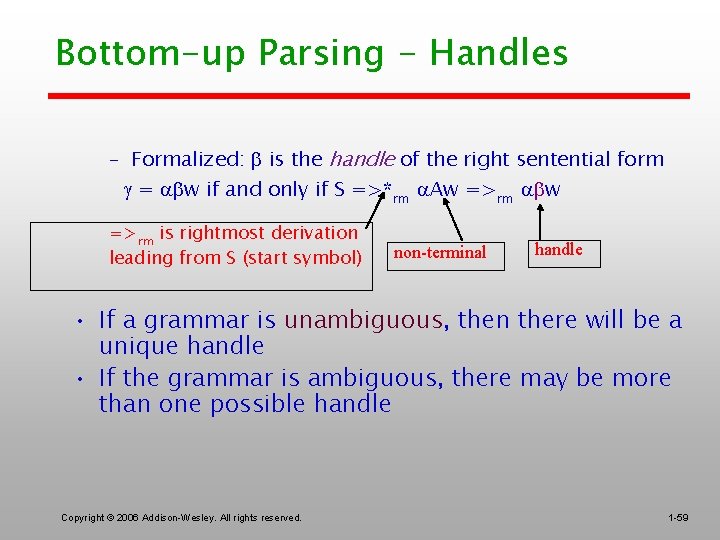
Bottom-up Parsing - Handles – Formalized: is the handle of the right sentential form = w if and only if S =>*rm Aw =>rm is rightmost derivation leading from S (start symbol) non-terminal handle • If a grammar is unambiguous, then there will be a unique handle • If the grammar is ambiguous, there may be more than one possible handle Copyright © 2006 Addison-Wesley. All rights reserved. 1 -59

Back to our simple example • Example grammar and derivation: S -> a. Ac A -> a. A | b S => a. Ac => aabc • Bottom-up parse: aabc => aa. Ac => S • Remember there’s an incorrect choice: aabc => aa. Ac => a. S So how can we choose the right handle? • Bottom-up is based on rightmost derivation • Second option is not a rightmost derivation • Insight is to identify a phrase (next slide…)* * the tool actually does this for us… Copyright © 2006 Addison-Wesley. All rights reserved.

Phrases • A phrase is a sub-sequence of a sentential form that is eventually “reduced” to a non-terminal • A simple phrase can be reduced in one step • The handle is the left-most simple phrase • Example: S => a. Ac => aabc S A a a A sentential form b c In this sentential form, what are the: • phrases • simple phrases • handle So if we have the parse tree, it’s easy to identify the handle. But how do we do it when we’re reading input from left to right? May need to delay decision, read input until find handle.

Phrases – Quick Exercise • Example grammar and derivation: S -> a. AC A -> a. A | b C -> c S => a. AC => a. Ac => aabc S A a a A C In this sentential form, what are the: • phrases • simple phrases • handle (leftmost simple phrase) sentential form b c Copyright © 2006 Addison-Wesley. All rights reserved.

Bottom-up Parsing (cont. ) • For bottom-up parsing, need to decide: – when to reduce – what production (rule) to apply • Shift-Reduce Algorithms – Reduce is the action of replacing the handle on the top of the parse stack with its corresponding LHS – Shift is the action of moving the next token to the top of the parse stack • Every parser is a pushdown automaton (PDA) – can recognize a context-free grammar Copyright © 2006 Addison-Wesley. All rights reserved. 1 -63

Bottom-up Parsing (cont. ) • Knuth’s insight: A bottom-up parser could use the entire history of the parse, up to the current point, to make parsing decisions – Finite, relatively small number of different possible parse situations – Store history on the parse stack – No need to look to left and right of substring, can just look to the left S A a a A c b • LR parsers must be constructed with a tool Copyright © 2006 Addison-Wesley. All rights reserved. 1 -64

Bottom-up Parsing (cont. ) • • An LR configuration stores the state of an LR parser Ss is a parser state (from a table - you’ll see) Xs is a grammar symbol (from our CFG) as are input symbols (from the string) (S 0 X 1 S 1 X 2 S 2… Xm. Sm, aiai+1…an$) (S 0 X 1 S 1 X 2 S 2… A->b. Sm, baiai+1…an$) • A reduction step is triggered when we see the symbols corresponding to a rule’s RHS on the top of the stack Copyright © 2006 Addison-Wesley. All rights reserved. 1 -65

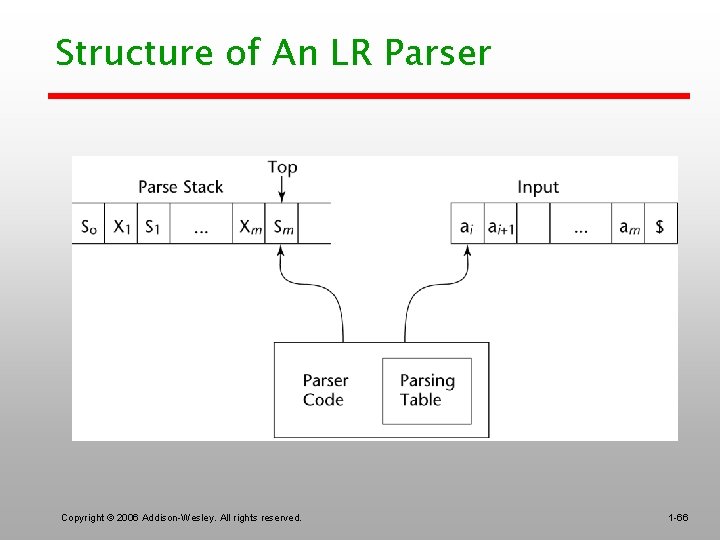
Structure of An LR Parser Copyright © 2006 Addison-Wesley. All rights reserved. 1 -66

Bottom-up Parsing (cont. ) • LR parsers are table driven, where the table has two components, an ACTION table and a GOTO table – The ACTION table specifies the action of the parser, given the parser state and the next token • Rows are state names; columns are terminals – The GOTO table specifies which state to put on top of the parse stack after a reduction action is done • Rows are state names; columns are nonterminals Copyright © 2006 Addison-Wesley. All rights reserved. 1 -67

Bottom-up Parsing (cont. ) stack input • Initial configuration: (S 0, a 1…an$) • Parser actions: – (S 0 X 1 S 1 X 2 S 2…Sm. Xm, aiai+1…an$) – If ACTION[Sm, ai] = Shift S, the next new stack top configuration is: (S 0 X 1 S 1 X 2 S 2…Sm. Xm. Sai, ai+1…an$) – If ACTION[Sm, ai] = Reduce A and S = GOTO[Sm-r, A], where r = the length of , the new stack top next configuration is (S 0 X 1 S 1 X 2 S 2…Xm-r. Sm-r. AS, aiai+1…an$) was popped off stack Copyright © 2006 Addison-Wesley. All rights reserved. 1 -68

Bottom-up Parsing (cont. ) • Parser actions (continued): – If ACTION[Sm, ai] = Accept, the parse is complete and no errors were found. – If ACTION[Sm, ai] = Error, the parser calls an error-handling routine. Copyright © 2006 Addison-Wesley. All rights reserved. 1 -69

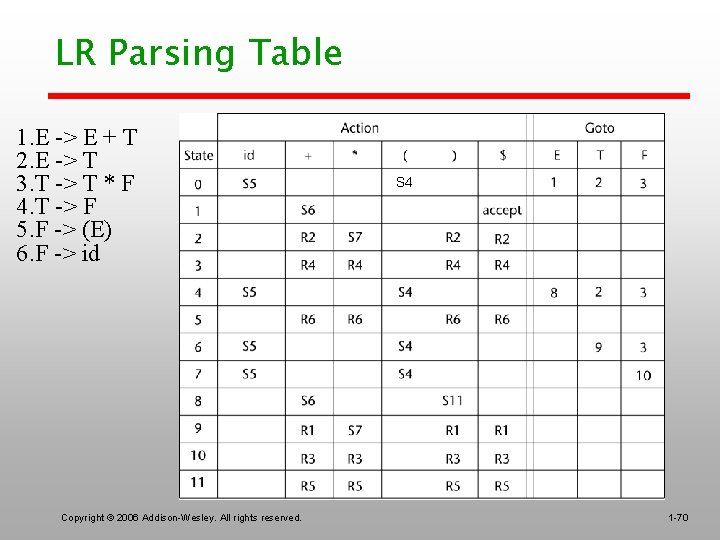
LR Parsing Table 1. E -> E + T 2. E -> T 3.

Bottom-up Parsing/LR example Parse id + id * id Stack 0 0 id 5 0 F 3 0 T 2 0 E 1 +6 id 5 0 E 1 +6 F 3 0 E 1 +6 T 9 *7 id 5 0 E 1 +6 T 9 *7 F 10 0 E 1 +6 T 9 0 E 1 (see Chapter 4 Parsing. ppt, start slide 14) Input id + id * id$ + id * id$ * id$ $ $ Copyright © 2006 Addison-Wesley. All rights reserved. Action S 5 R 6 (use GOTO[0. F]) R 4 (use GOTO[0, T]) R 2 (use GOTO[0, E]) S 6 S 5 R 6 (use GOTO[6, F]) R 4 (use GOTO[6, T] S 7 S 5 R 6 (use GOTO[7. F]) R 3 (use GOTO[6, T]) R 1 (use GOTO[0. E]) accept 1 -71

Bottom-up Parsing/ LR parsers • LR parsers use a relatively small program and a parsing table • Advantages of LR parsers: – They will work for nearly all grammars that describe programming languages. – They work on a larger class of grammars than other bottom-up algorithms, but are as efficient as any other bottom-up parser. – They can detect syntax errors as soon as it is possible in left-to-right scan – The LR class of grammars is a superset of the class parsable by LL parsers. Copyright © 2006 Addison-Wesley. All rights reserved. 1 -72

Bottom-up Parsing (cont. ) • A parser table can be generated from a given grammar with a tool, e. g. , yacc • To find out more about building the LR tables, read Engineering a Compiler or comparable compiler textbook. Copyright © 2006 Addison-Wesley. All rights reserved. 1 -73