CS 39 R SingleSided Surfaces Carlo H Squin























- Slides: 44

CS 39 R Single-Sided Surfaces Carlo H. Séquin EECS Computer Science Division University of California, Berkeley

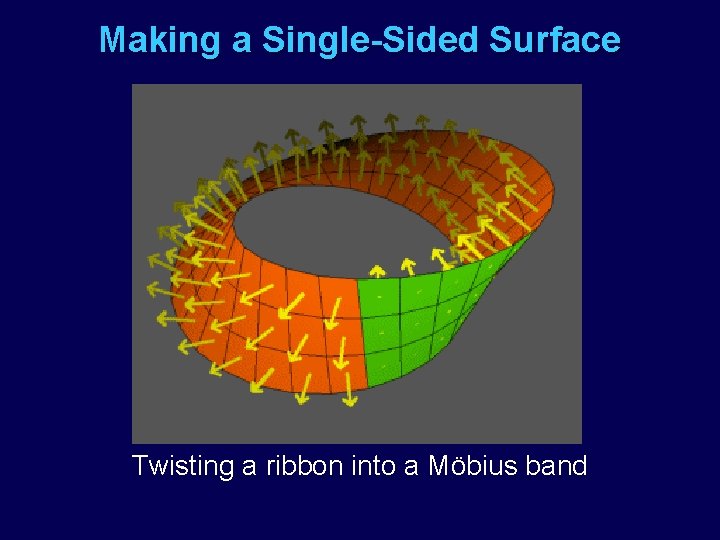
Making a Single-Sided Surface Twisting a ribbon into a Möbius band

Simple Möbius Bands u A single-sided surface with a single edge: A closed ribbon with a 180°flip. A closed ribbon with a 540°flip.

More Möbius Bands Max Bill’s sculpture of a Möbius band. The “Sue-Dan-ese” M. B. , a “bottle” with circular rim.

A Möbius Band Transfromation Widen the bottom of the band by pulling upwards its two sides, get a Möbius basket, and then a Sudanese Möbius band.

Many Different Möbius Shapes Left-twisting versions shown – can be smoothly transformed into one another u Topologically, these are all equivalent: They all are single-sided, They all have ONE rim, They all are of genus ONE, and E. C. = 0. u Each shape is chiral: its mirror image differs from the original.

These are NOT Möbius Bands ! u What you may find on the Web under “Möbius band” (1):

These are NOT Möbius Bands ! u What you may find on the Web under “Möbius band” (2):

These are NOT Möbius Bands ! u What you may find on the Web under “Möbius band” (3):

TWO Möbius Bands ! u Two Möbius bands that eventually get fused together:

Topological Surface Classification The distinguishing characteristics: u Is it two-sided, orientable – or single-sided, non-orientable? u Does it have rims? – How many separate closed curves? u What is its genus? – How many handles or tunnels? u Is it smooth – or does it have singularities (e. g. creases)? Can we make a single-sided surface with NO rims?

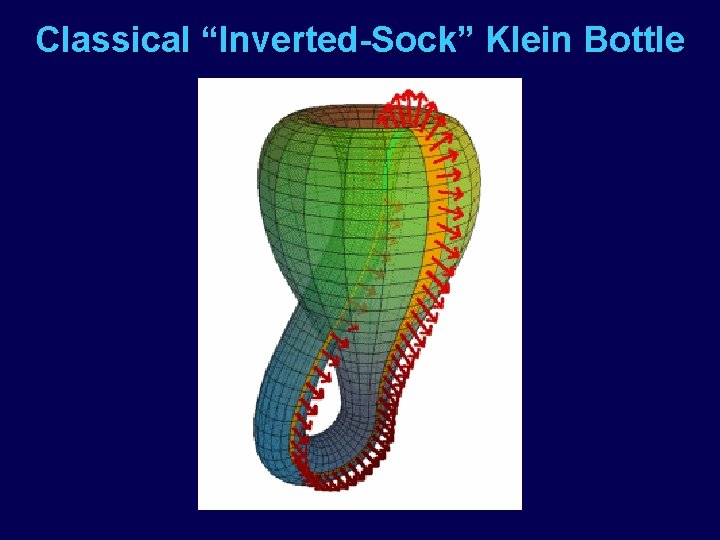
Classical “Inverted-Sock” Klein Bottle

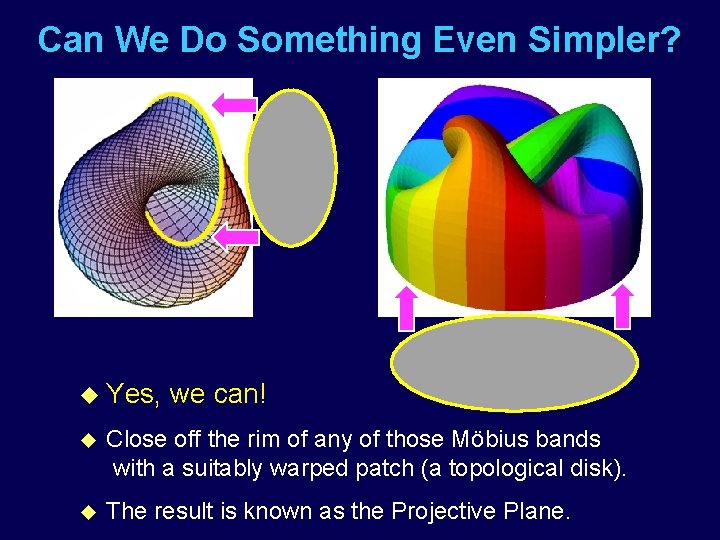
Can We Do Something Even Simpler? u Yes, we can! u Close off the rim of any of those Möbius bands with a suitably warped patch (a topological disk). u The result is known as the Projective Plane.

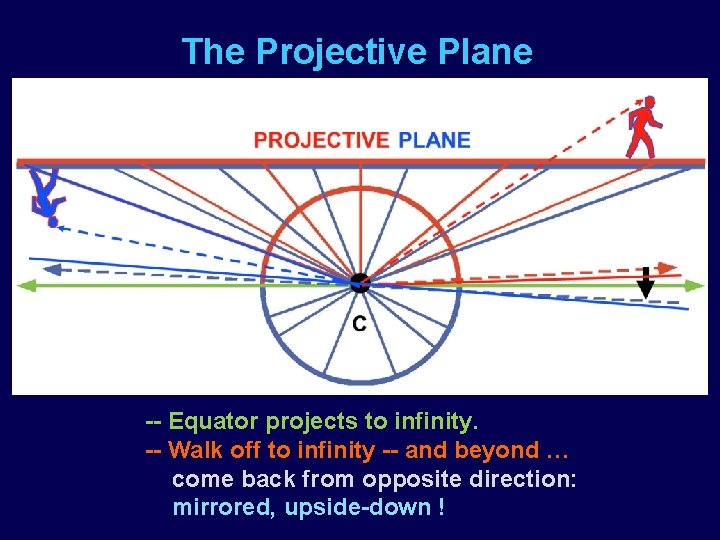
The Projective Plane -- Equator projects to infinity. -- Walk off to infinity -- and beyond … come back from opposite direction: mirrored, upside-down !

The Projective Plane is a Cool Thing! u It is single-sided: Flood-fill paint flows to both faces of the plane. u It is non-orientable: Shapes passing through infinity get mirrored. u. A straight line does not cut it apart! One can always get to the other side of that line by traveling through infinity. u It is infinitely large! (somewhat impractical) It would be nice to have a finite model with the same topological properties. . .

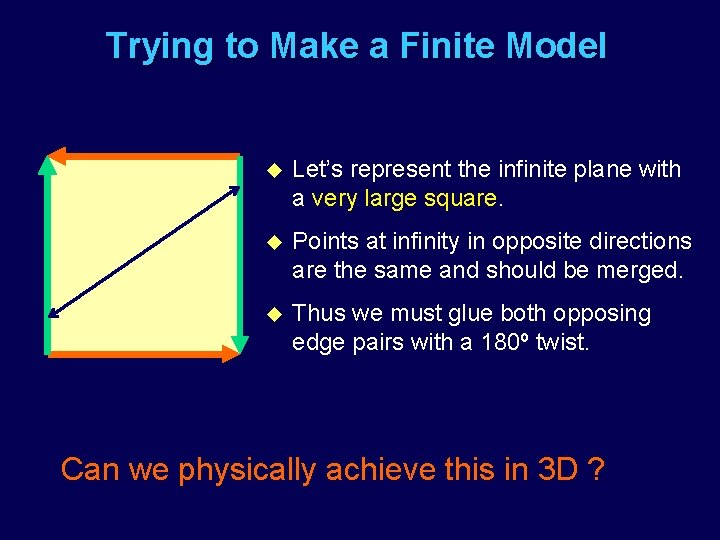
Trying to Make a Finite Model u Let’s represent the infinite plane with a very large square. u Points at infinity in opposite directions are the same and should be merged. u Thus we must glue both opposing edge pairs with a 180º twist. Can we physically achieve this in 3 D ?

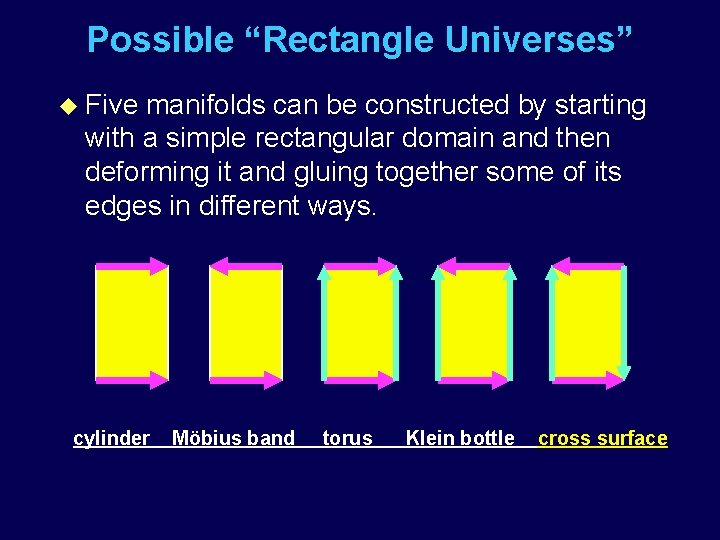
Possible “Rectangle Universes” u Five manifolds can be constructed by starting with a simple rectangular domain and then deforming it and gluing together some of its edges in different ways. cylinder Möbius band torus Klein bottle cross surface

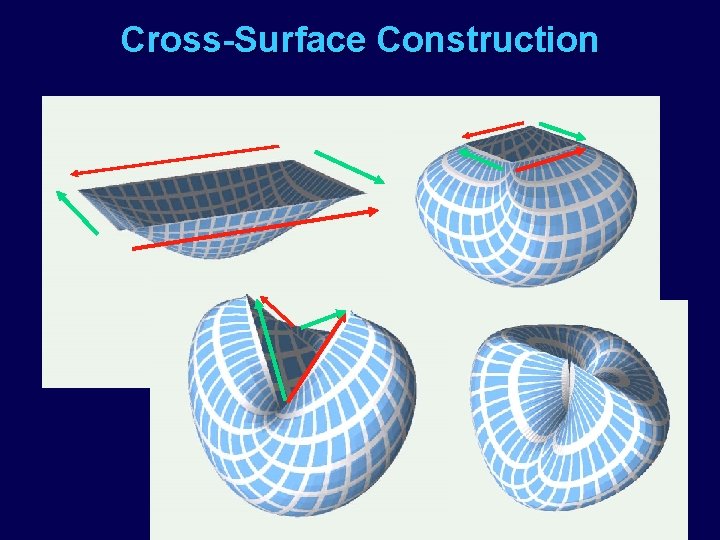
Cross-Surface Construction

Wood / Gauze Model of Projective Plane Cross-Surface = “Cross-Cap” + punctured sphere

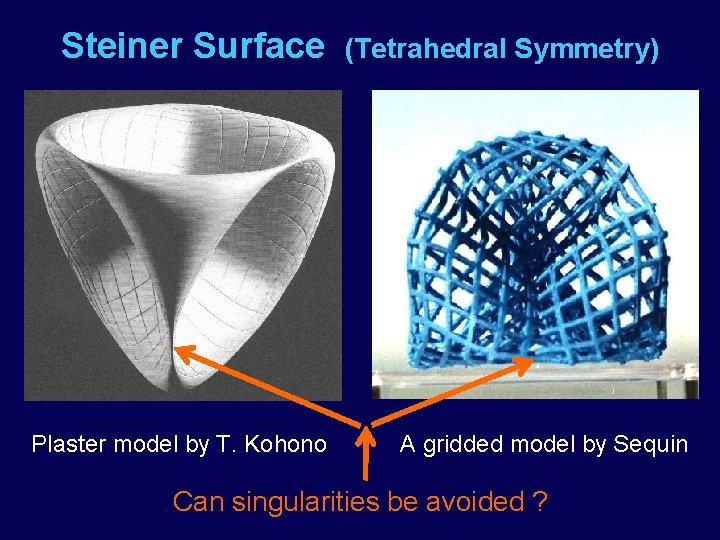
Cross-Cap Imperfections u Has 2 singular points with infinite curvature. u Can this be avoided?

Steiner Surface Plaster model by T. Kohono (Tetrahedral Symmetry) A gridded model by Sequin Can singularities be avoided ?

Can Singularities be Avoided ? Werner Boy, a student of Hilbert, was asked to prove that it cannot be done. But he found a solution in 1901 ! u It has 3 self-intersection loops. u It has one triple point, where 3 surface branches cross. u It may be modeled with 3 -fold symmetry.

Various Models of Boy’s Surface

Main Characteristics of Boy’s Surface Key Features: u Smooth u One u 3 everywhere! triple point, intersection loops emerging from it.

Projective Plane With a Puncture The projective plane minus a disk is: u a Möbius band; u or a cross-cap; u or a Boy cap. u. This u makes a versatile building block! with an open rim by which it can be grafted onto other surfaces.

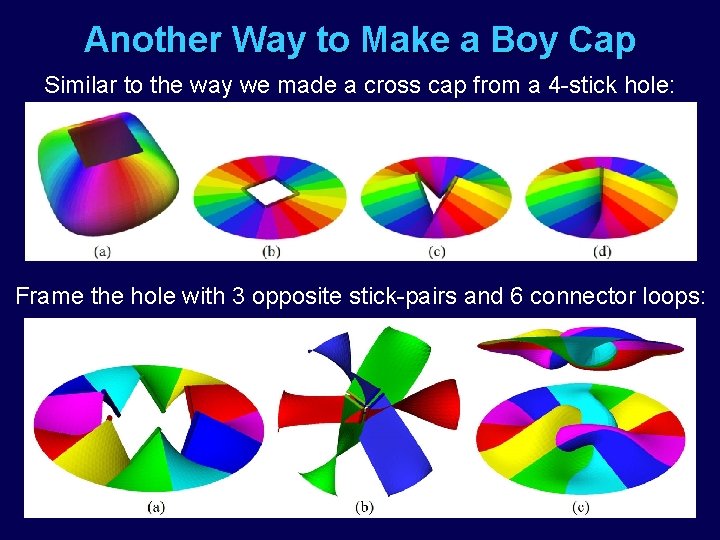
Another Way to Make a Boy Cap Similar to the way we made a cross cap from a 4 -stick hole: Frame the hole with 3 opposite stick-pairs and 6 connector loops:

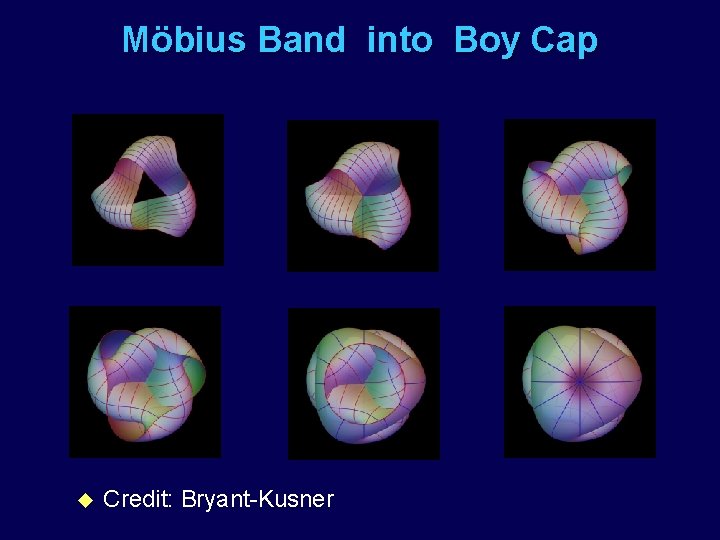
Mӧbius Band into Boy Cap u Credit: Bryant-Kusner

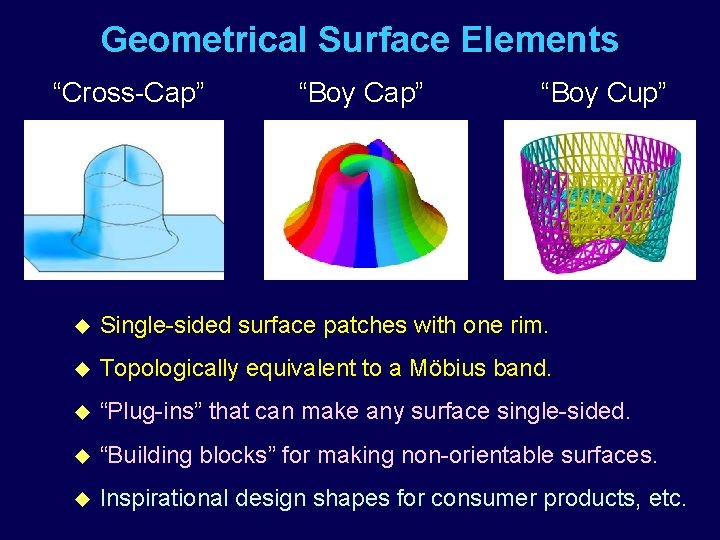
Geometrical Surface Elements “Cross-Cap” “Boy Cup” u Single-sided surface patches with one rim. u Topologically equivalent to a Möbius band. u “Plug-ins” that can make any surface single-sided. u “Building blocks” for making non-orientable surfaces. u Inspirational design shapes for consumer products, etc.

u In summary: Boy Cap + Disk = Boy Surface Mӧbius Band + Disk = Projective Plane Genus = 1; E. C. = 1 u And: TWO Mӧbius Bands = Klein Bottle Genus = 2; E. C. = 0 See:

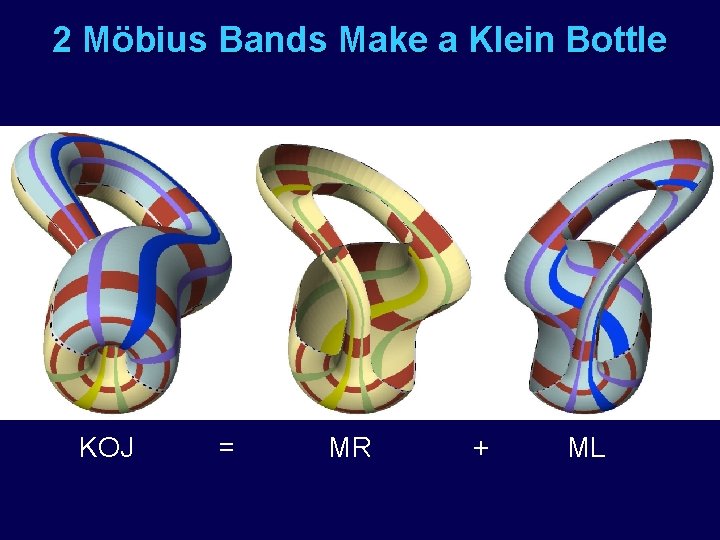
2 Möbius Bands Make a Klein Bottle KOJ = MR + ML

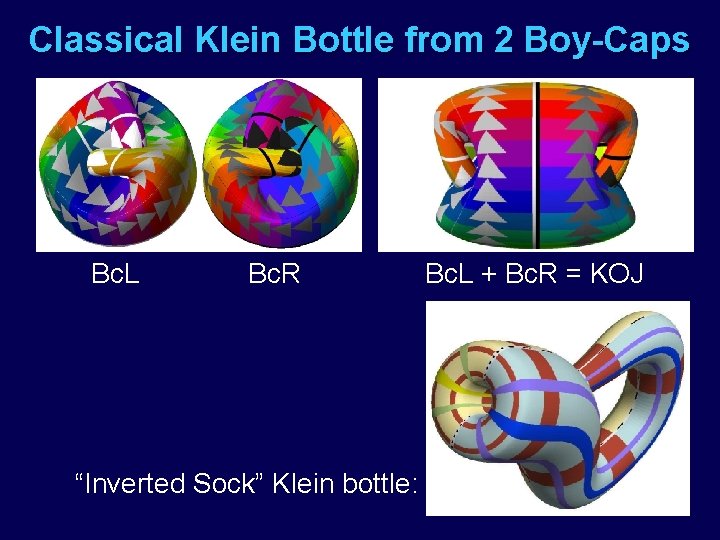
Classical Klein Bottle from 2 Boy-Caps Bc. L Bc. R “Inverted Sock” Klein bottle: Bc. L + Bc. R = KOJ

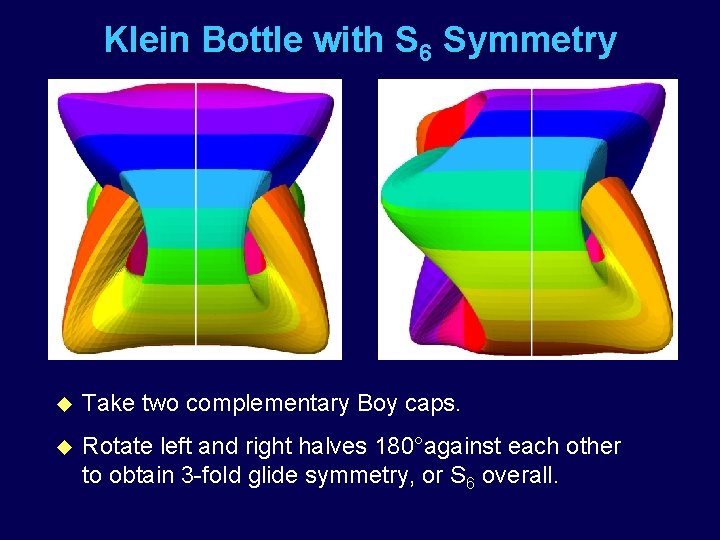
Klein Bottle with S 6 Symmetry u Take two complementary Boy caps. u Rotate left and right halves 180°against each other to obtain 3 -fold glide symmetry, or S 6 overall.

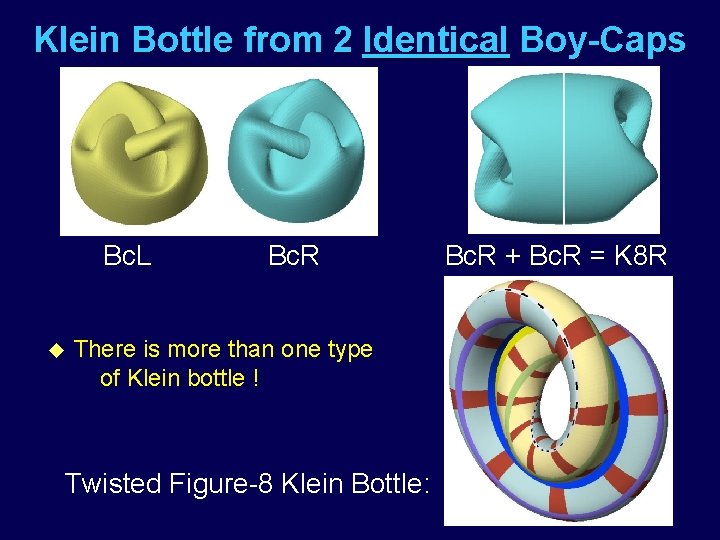
Klein Bottle from 2 Identical Boy-Caps Bc. L u Bc. R There is more than one type of Klein bottle ! Twisted Figure-8 Klein Bottle: Bc. R + Bc. R = K 8 R

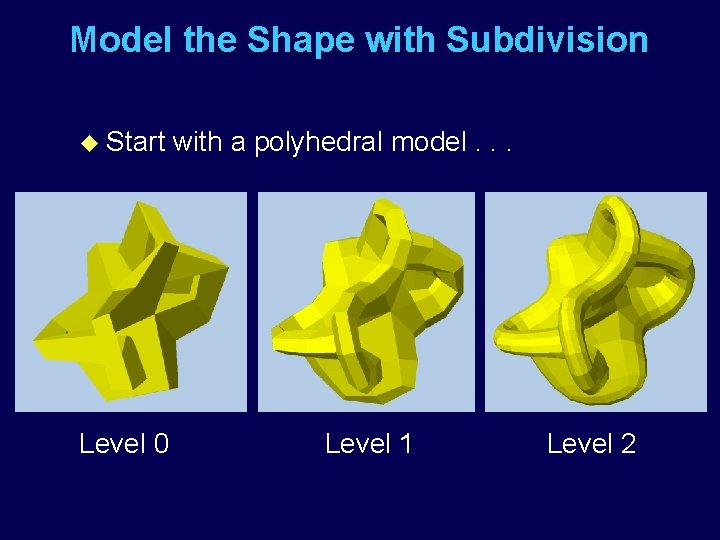
Model the Shape with Subdivision u Start Level 0 with a polyhedral model. . . Level 1 Level 2

Make a Gridded Sculpture!

Increase the Grid Density

Actual Sculpture Model

S 6 Klein Bottle Rendered by C. Mouradian http: //netcyborg. free. fr/

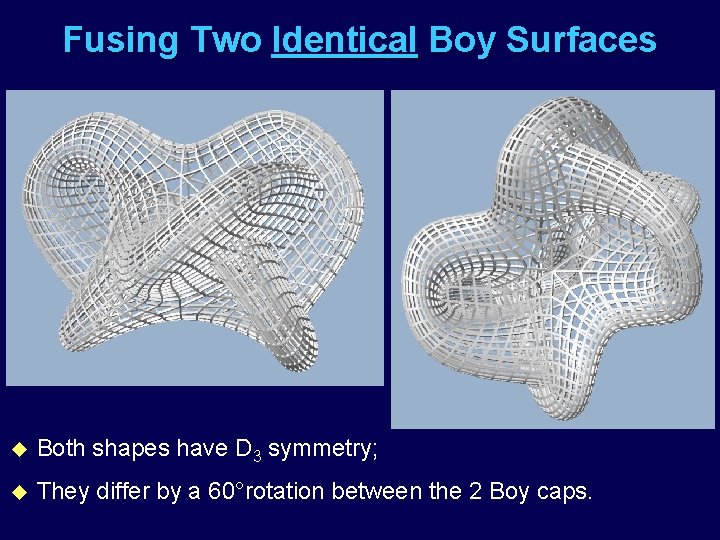
Fusing Two Identical Boy Surfaces u Both shapes have D 3 symmetry; u They differ by a 60°rotation between the 2 Boy caps.

Building Blocks To Make Any Surface u. A sphere to start with; u. A hole-punch to make punctures: Each decreases Euler Characteristic by one. u We can fill these holes again with: l Disks: Increases Euler Characteristic by one. l Cross-Caps: Makes surface single-sided. l Boy-caps: Makes surface single-sided. l Handles (btw. 2 holes): Orientability unchanged. l Cross-Handles (btw. 2 holes): Makes surface single-sided. Genus changes; E. C. unchanged.

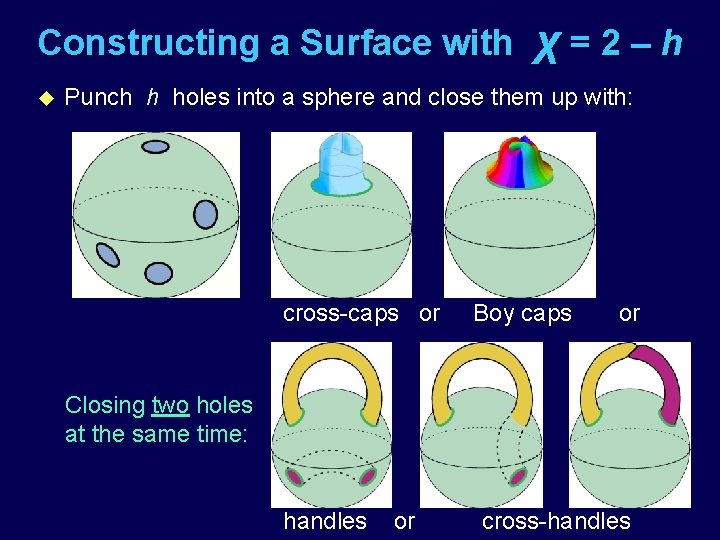
Constructing a Surface with u χ=2‒h Punch h holes into a sphere and close them up with: cross-caps or Boy caps or Closing two holes at the same time: handles or cross-handles

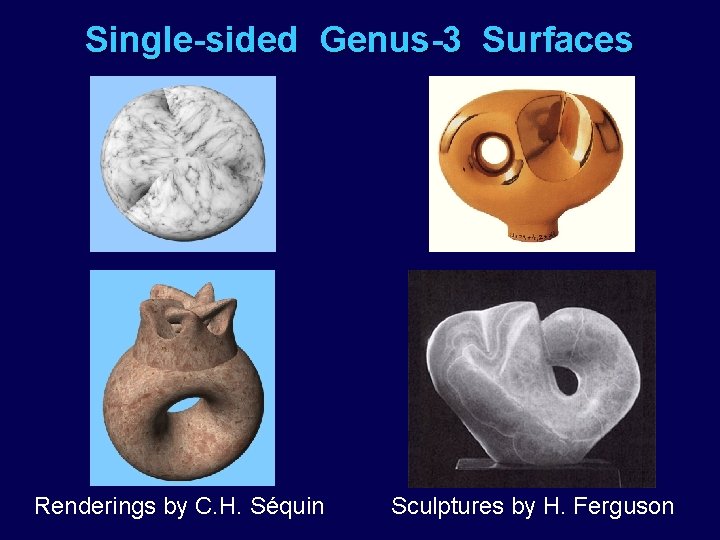
Single-sided Genus-3 Surfaces Renderings by C. H. Séquin Sculptures by H. Ferguson

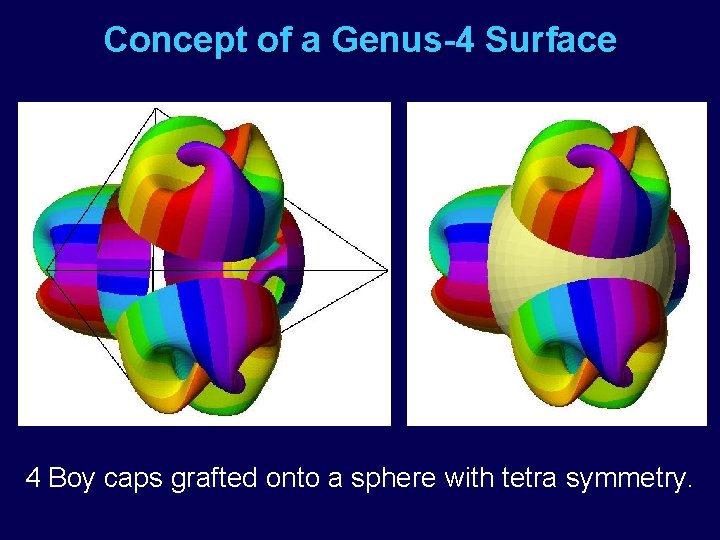
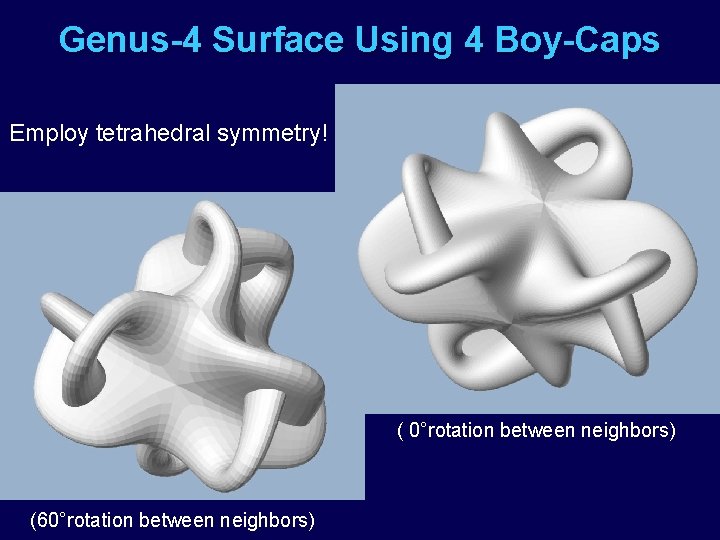
Concept of a Genus-4 Surface 4 Boy caps grafted onto a sphere with tetra symmetry.

Genus-4 Surface Using 4 Boy-Caps Employ tetrahedral symmetry! ( 0°rotation between neighbors) (60°rotation between neighbors)
 Squin sa switzerland
Squin sa switzerland Clipping algorithms are used to remove hidden surfaces
Clipping algorithms are used to remove hidden surfaces Left surface of heart
Left surface of heart Friction can act between two unmoving, touching surfaces.
Friction can act between two unmoving, touching surfaces. The relative lightness and darkness of surfaces.
The relative lightness and darkness of surfaces. What are patent impressions
What are patent impressions Nationalism surfaces in india
Nationalism surfaces in india Pyramid examples
Pyramid examples Walking and working surfaces quiz
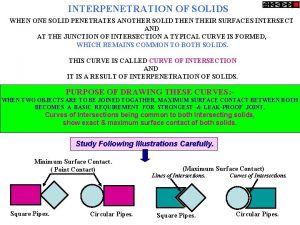
Walking and working surfaces quiz When a solid completely penetrates another solid
When a solid completely penetrates another solid Yz plane equation
Yz plane equation Subdivision surfaces in character animation
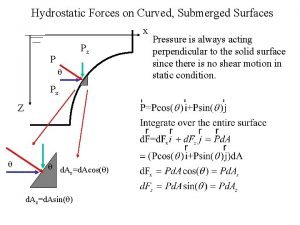
Subdivision surfaces in character animation Hydrostatic force on surface
Hydrostatic force on surface The refractive indices of crown glass prism for c d f
The refractive indices of crown glass prism for c d f Geometric charting dental
Geometric charting dental Laws of access cavity preparation
Laws of access cavity preparation 3 things that have 6 faces and 8 vertices
3 things that have 6 faces and 8 vertices Friction
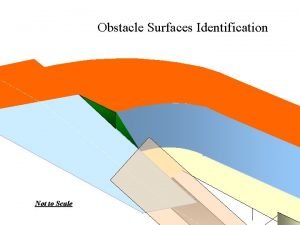
Friction Obstacle identification surface
Obstacle identification surface How is tool mark impression evidence examined
How is tool mark impression evidence examined Texture refers to the physical and visual qualities of a
Texture refers to the physical and visual qualities of a Normal inclined and oblique surfaces
Normal inclined and oblique surfaces Computer graphics
Computer graphics Famous forensic odontology cases
Famous forensic odontology cases Walking working surfaces
Walking working surfaces Femur borders and surfaces
Femur borders and surfaces The splitting of a mineral along smooth flat surfaces
The splitting of a mineral along smooth flat surfaces Statistical surface can be
Statistical surface can be Inclined surfaces in orthographic projections
Inclined surfaces in orthographic projections Quadric surfaces chart
Quadric surfaces chart Mark made when surfaces slide across one another:
Mark made when surfaces slide across one another: Aircraft control surfaces and components
Aircraft control surfaces and components Parallel line development method
Parallel line development method Interpenetration drawing
Interpenetration drawing Reconfigurable intelligent surfaces
Reconfigurable intelligent surfaces Inclined surfaces in orthographic projections
Inclined surfaces in orthographic projections Walking on slippery surfaces
Walking on slippery surfaces Quadratic surfaces
Quadratic surfaces Imaginary surfaces
Imaginary surfaces Surfaces of thyroid gland
Surfaces of thyroid gland Development of lateral surfaces
Development of lateral surfaces Reflection of light at plane surface
Reflection of light at plane surface Ellispsoid
Ellispsoid Cylinder heat transfer
Cylinder heat transfer What are the three main types of body membranes
What are the three main types of body membranes