Waterloo March 2017 Artistic Geometry Carlo H Squin

Waterloo, March 2017 Artistic Geometry Carlo H. Séquin EECS Computer Sciences University of California, Berkeley

Basel, Switzerland MNG

Jakob Bernoulli (1654‒ 1705) Logarithmic Spiral

Leonhard Euler (1707‒ 1783) Imaginary Numbers

Descriptive Geometry

“Re-creations” of Inspiring Art Alexander Calder: Mobiles C. H. Séquin, circa 1957

String Sculptures u ? : Naum Gabo String Sculptures C. H. Séquin, circa 1977

Orderly Tangles Alan Holden “Glowing Tetra. Tangle” C. H. Séquin (1983)

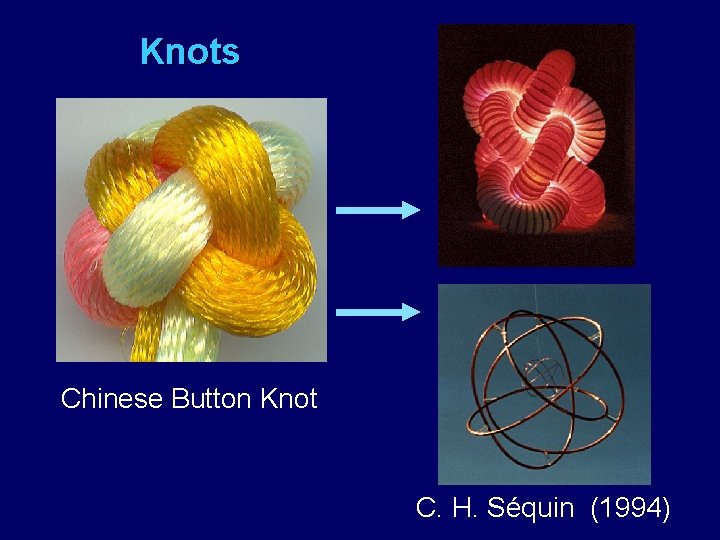
Knots Chinese Button Knot C. H. Séquin (1994)

Simple Geometry u Max Bill FDM Models by C. H. Séquin (2000)

Ribbon Sculptures Altamont Brent Collins: Pax Mundi (1994) Stelvio

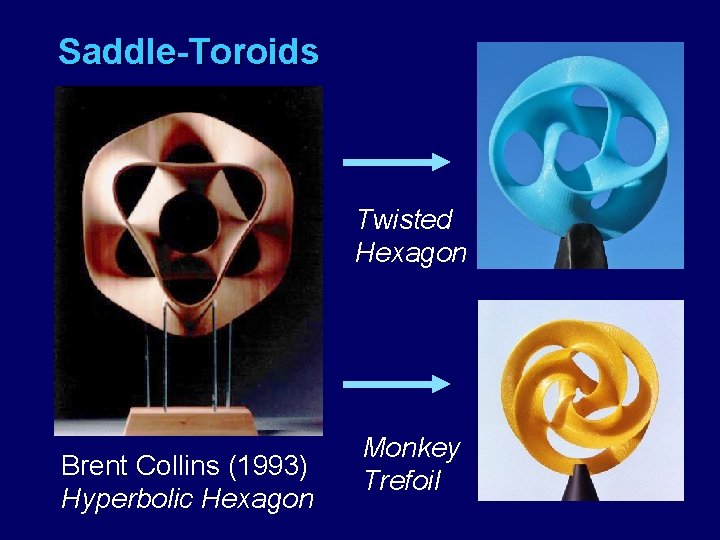
Saddle-Toroids Twisted Hexagon Brent Collins (1993) Hyperbolic Hexagon Monkey Trefoil

Brent Collins (1997) “Hyperbolic Hexagon II”

Brent Collins: Stacked Saddles All photos by Phillip Geller

The Math in Collins’ Sculptures u Collins works with rulers and compasses; any math in his early work is intuitive. u He is inspired by nature, e. g. soap films (= minimal area surfaces). u Prof. George Francis: “Connection to math. Minimal Surfaces!”

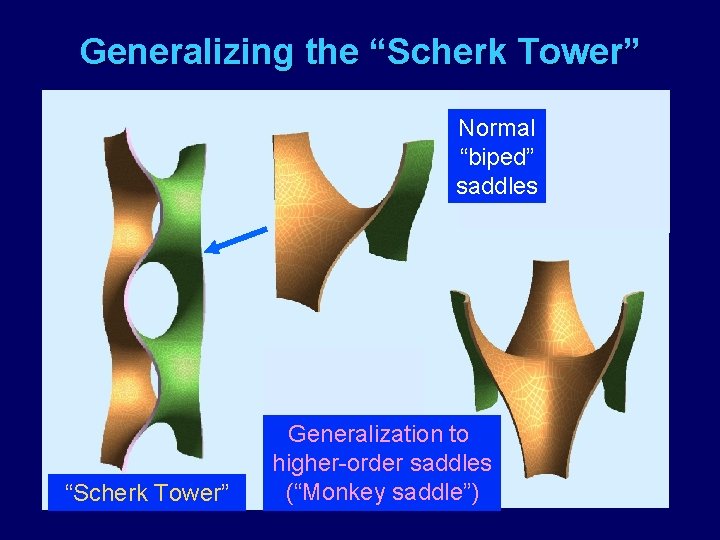
Scherk’s 2 nd Minimal Surface (1834) u The central part of this is a “Scherk Tower. ”

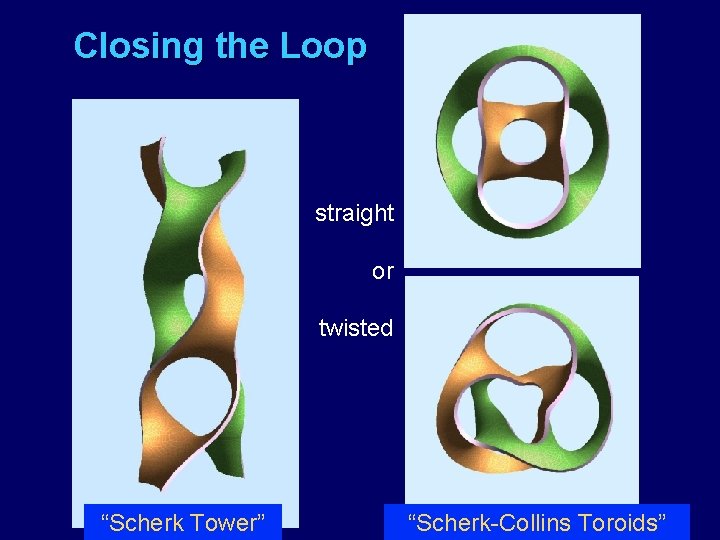
Generalizing the “Scherk Tower” Normal “biped” saddles “Scherk Tower” Generalization to higher-order saddles (“Monkey saddle”)

Closing the Loop straight or twisted “Scherk Tower” “Scherk-Collins Toroids”

Brent Collins: Hyperbolic Hexagon (1993) Six balanced saddles in a circular ring. Inspired by the shape of a soap film suspended in a wire frame. = Warped “Scherk Tower” (with 6 stories).

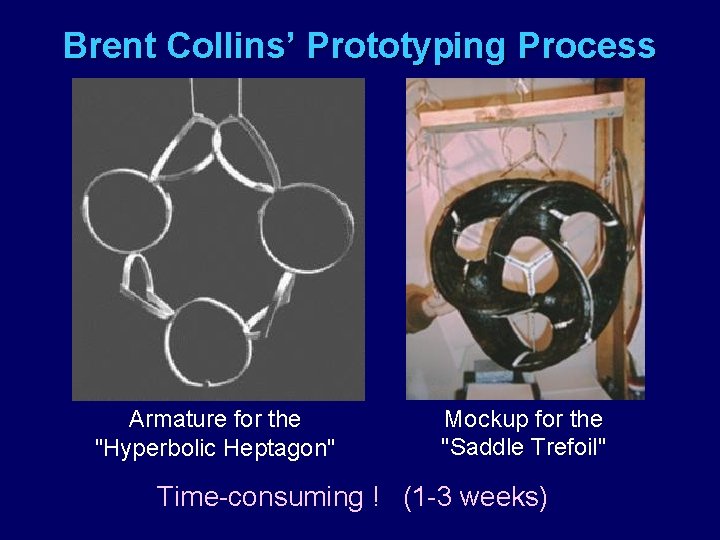
Brent Collins’ Prototyping Process Armature for the "Hyperbolic Heptagon" Mockup for the "Saddle Trefoil" Time-consuming ! (1 -3 weeks)

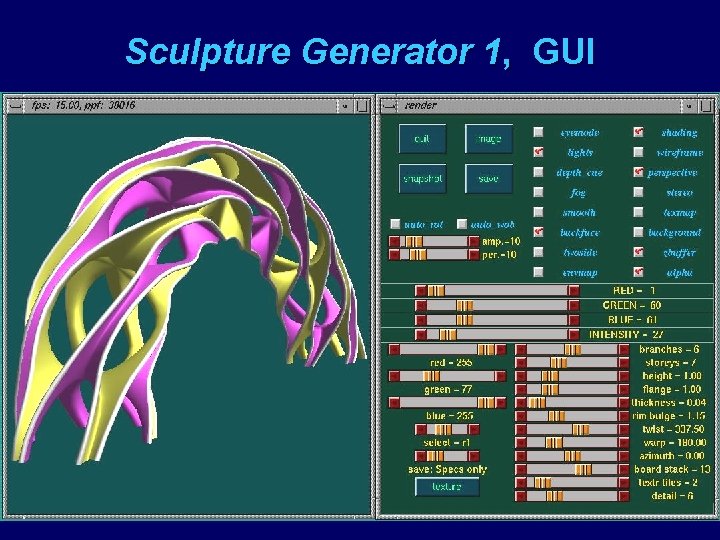
Sculpture Generator 1, GUI

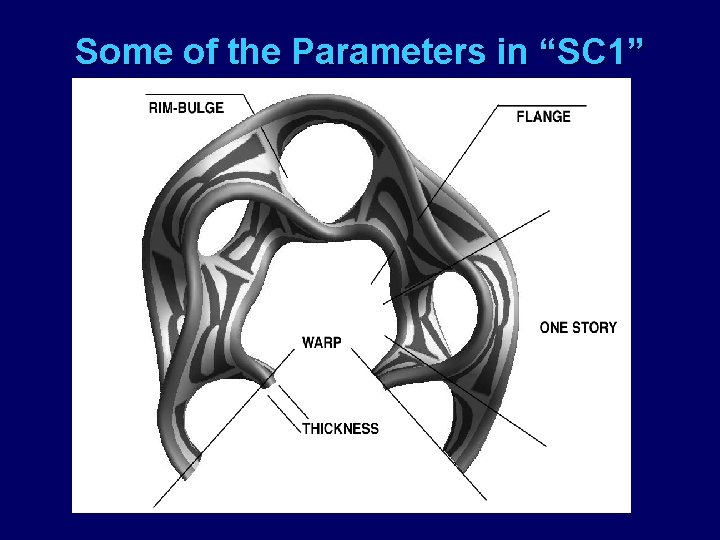
Some of the Parameters in “SC 1”

Generated Scherk-Collins Shapes

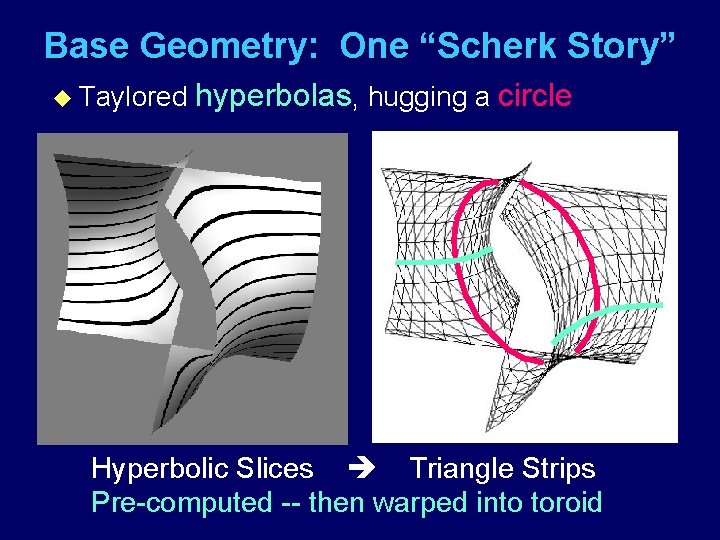
Base Geometry: One “Scherk Story” u Taylored hyperbolas, hugging a circle Hyperbolic Slices Triangle Strips Pre-computed -- then warped into toroid

Shapes from Sculpture Generator 1

Collins’ Fabrication Process Layered laminated main shape Wood master pattern for sculpture Example: “Vox Solis”

Slices through “Minimal Trefoil” 50% 30% 23% 10% 45% 27% 20% 5% 35% 25% 15% 2%

Profiled Slice through “Heptoroid” u One thick slice thru sculpture, from which Brent can cut boards and assemble a rough shape. u Traces represent: top and bottom, as well as cuts at 1/4, 1/2, 3/4 of one board.

Emergence of the Heptoroid (1) Assembly of the precut boards

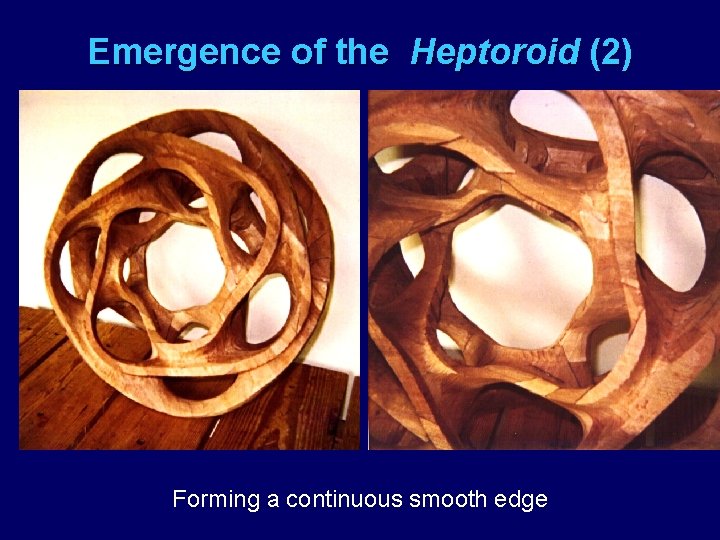
Emergence of the Heptoroid (2) Forming a continuous smooth edge

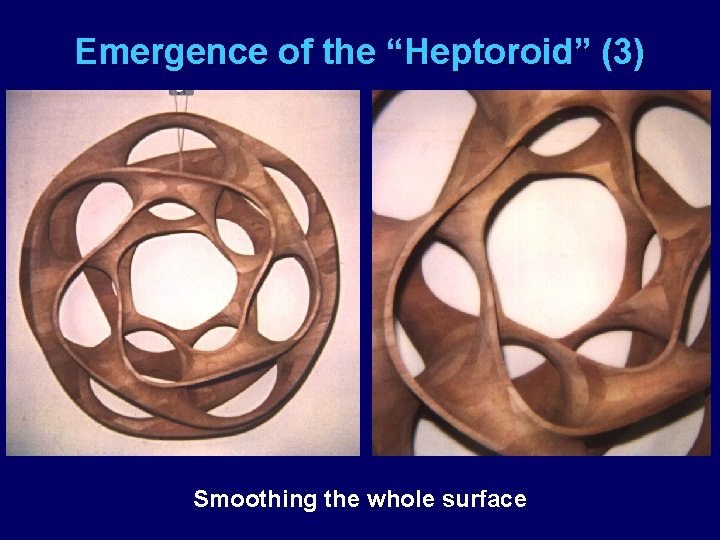
Emergence of the “Heptoroid” (3) Smoothing the whole surface

The Finished Heptoroid u at Fermi Lab Art Gallery (1998).

Inauguration Sutardja Dai Hall 2/27/09

“Scherk-Collins” Sculptures (FDM)

Cohesion SIGGRAPH’ 2003 Art Gallery

Hypersculpture: Family of 12 Trefoils W=2 W=1 B=2 B=3 B=4

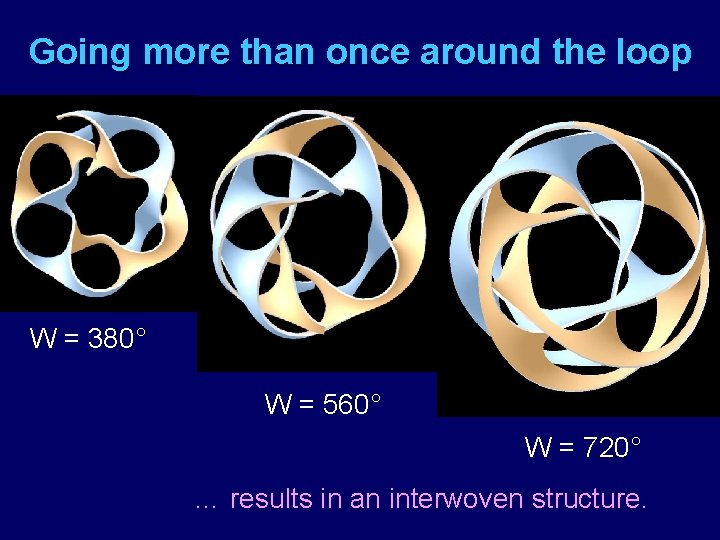
Going more than once around the loop W = 380° W = 560° W = 720° … results in an interwoven structure.

11 Stories, Monkey-Saddles, W=2: cross–eye stereo picture

9 -story Intertwined Double Toroid Bronze investment casting from wax original made on 3 D Systems’ “Thermojet”

Extension of Concept Allow different kinds of “stretching” …

Extending the Paradigm: Totem 3 Bronze Investment Cast

Stepwise Expansion of Horizon u Playing with many different shapes and u experimenting at the limit of the domain of the sculpture generator, u stimulates new ideas for alternative shapes and generating paradigms. Swiss Mountains

Sculpture Generator 1 as a Playground The computer becomes an amplifier / accelerator for the creative process.

V-art Virtual Glass Scherk Tower with Monkey Saddles (Radiance 40 hours) Jane Yen

Yet Another Medium: Stone Progress picture from Dingli Stone Carving Art Co. , SE China

Spring, 2012

The Viae Globi Series (Roads on a Sphere) u Another example how one special piece of art led to a computer program, which then allowed me to make a whole series of sculpture designs that all seem to belong to the same family.

Brent Collins’ Pax Mundi 1997: Wood, 30”diam. 2006: Commission from H&R Block, Kansas City to make a 70”diameter version in bronze. My task: Define the master geometry. CAD tools play important role!

How to Model Pax Mundi. . . u Already addressed that issue in 1998: u Pax Mundi could not be done with Sculpture Generator I u Needed u Used u First: a more general program ! the “Berkeley SLIDE” environment. Needed to find the basic paradigm

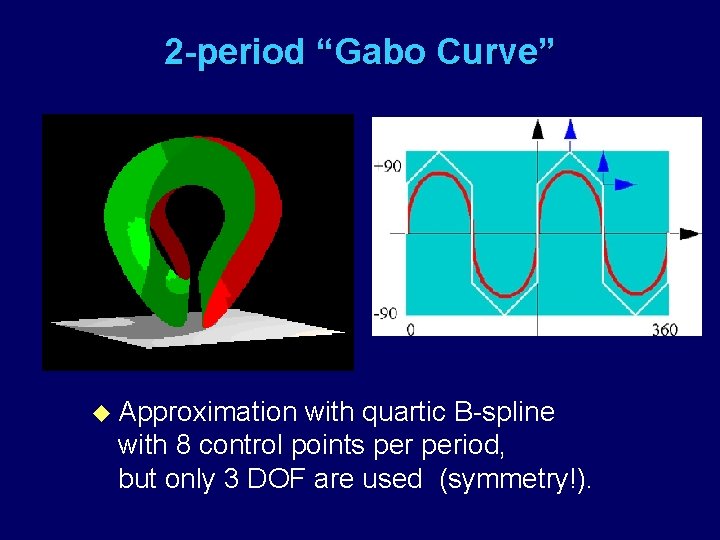
Sculptures by Naum Gabo Pathway on a sphere: Edge of surface is like seam of tennis- or base-ball; “ 2 -period Gabo curve. ”

2 -period “Gabo Curve” u Approximation with quartic B-spline with 8 control points period, but only 3 DOF are used (symmetry!).

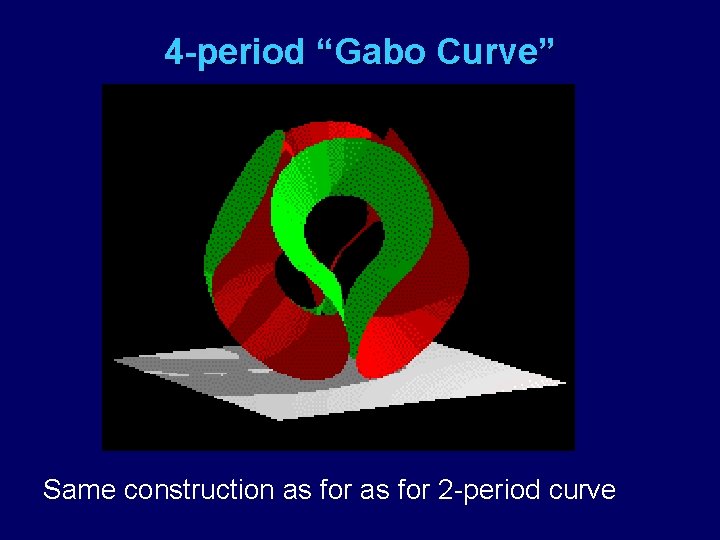
4 -period “Gabo Curve” Same construction as for 2 -period curve

Pax Mundi Revisited u Can be seen as: “Amplitude modulated, 4 -period Gabo curve”

Progressive Sweeps u Sculpture u There is not just a mathematical curve. is some substance; it has volume. u Define shape by sweeping a cross section along a given 3 D space curve.

SLIDE-GUI for “Pax Mundi” Shapes Good combination of interactive 3 D graphics and parameterizable procedural constructs.

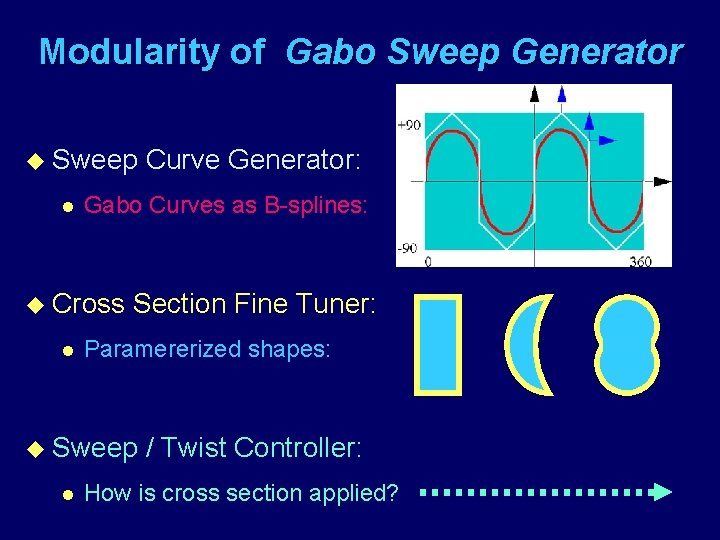
Modularity of Gabo Sweep Generator u Sweep l Gabo Curves as B-splines: u Cross l Section Fine Tuner: Paramererized shapes: u Sweep l Curve Generator: / Twist Controller: How is cross section applied?

Intrinsic Sweep Mode u Keep cross section perpendicular to tangent. u Place cross section into the x-y-plane of the Frenet frame. u Keep orientation / rotation as it was in the defining x-y-coordinate system. u Add any additional azimuth angle as a rotation around the z-axis (tangent).

Intrinsic Sweep Mode u Problems at inflection points (in plane): Pinched-off “hour-glass” shapes. “Natural” orientation with Frenet frame

Minimum-Torsion (-Rotation) Sweep u Project orientation of cross section forward, from one vertex of the sweep polyline to the next. u Neutralize rotation of Frenet frame intrinsic minimum torsion

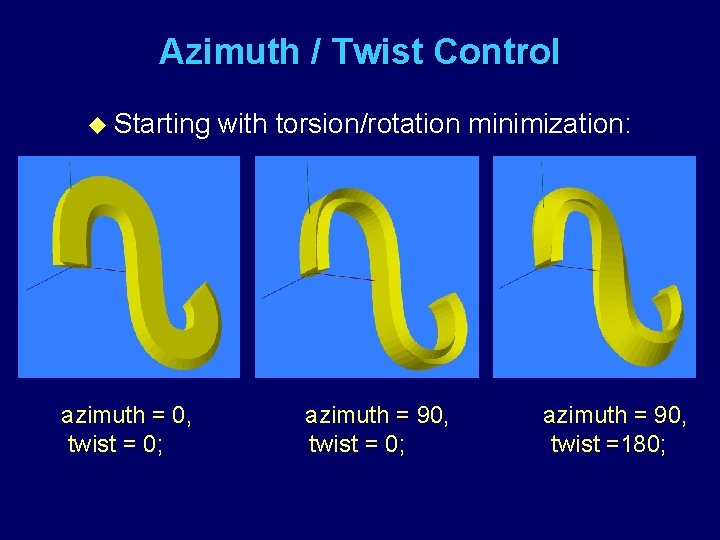
Azimuth / Twist Control u Starting azimuth = 0, twist = 0; with torsion/rotation minimization: azimuth = 90, twist = 0; azimuth = 90, twist =180;

Local Azimuth Control = “Warp” u Starting with torsion/rotation minimization: azimuth = 0, twist = 0; azimuth = 0, warp = -90;

Azimuth / Twist Control u Controls Natural orientation with Frenet frame applied to the 2 -period Gabo curve: Torsion Minimization: Azimuth: tangential / normal 900° of twist added.

Target Geometry (2007) Constraints: • Bronze, 70” diameter • Less than 1500 pounds • Less than $50’ 000 • Maintain beauty, strength • Minimize master geometry

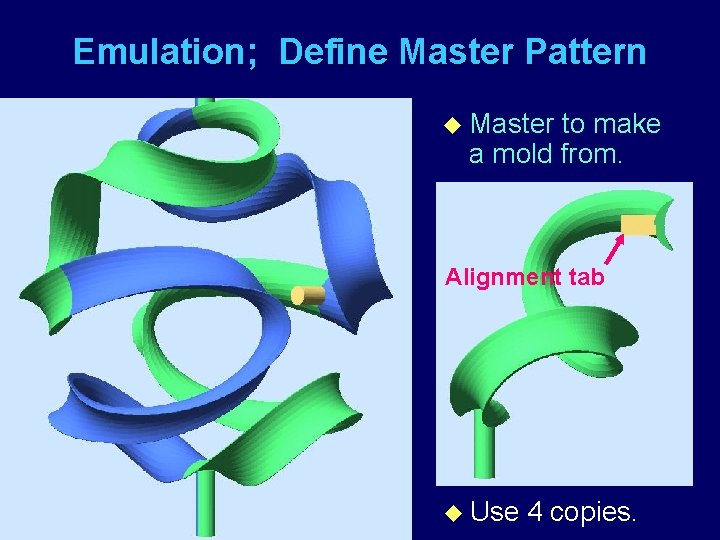
Emulation; Define Master Pattern u Master to make a mold from. Alignment tab u Use 4 copies.

Joe Valasek’s CNC Milling Machine u Styrofoam milling machine

Machined Master Pattern #2

(Cut) Master Silicone Rubber Mold

Mold Several (4) Wax Copies

Spruing the Wax Parts for Casting

Ceramic Slurry Shell Around Wax Part

Taking the Shell out of the Kiln

Shell Ready for Casting

The Pour

Casting with Liquid Bronze

Freeing the Bronze Cast

Assembling the Segments

The “Growing” Ribbon

Assembly Completed

Front Door of the. . . H&R Block Building

Steve Reinmuth, Bronze Studio, Eugene OR u http: //www. reinmuth. com/

Team effort: Brent Collins, Steve Reinmuth, Carlo Séquin

Extension: Free-form Curve on a Sphere Spherical Spline Path Editor (Jane Yen) Smooth interpolating curve through sparse data points

Many Different Viae Globi Models

Paradigm Extension: Sweep Path is no longer confined to a sphere! Chinese Button Knot

Chinese Button Knot (Knot 940) Bronze, Dec. 2007 Carlo Séquin cast & patina by Steve Reinmuth

Design Requires Paradigm Extension Music of the Spheres (Brent Collins)

Definition of Sweep Path (hugging 4 different spheres) Music of the Spheres (Brent Collins)

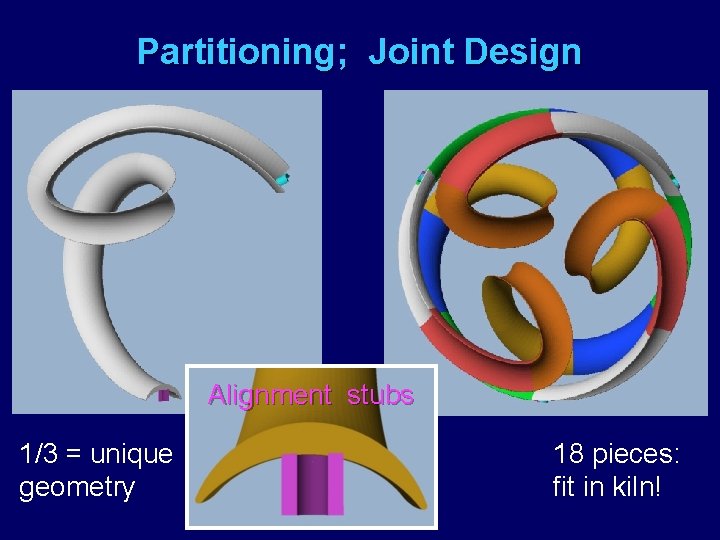
Partitioning; Joint Design Alignment stubs 1/3 = unique geometry 18 pieces: fit in kiln!

Some Segments Were Made Hollow This needs a double-walled tube mold!

Some of the Hollow Metal Parts

Assembly of Music of the Spheres

Installation at MWSU, Feb. 2013 Steve Reinmuth Brent Collins

Illuminated Music of the Spheres Photo by Phillip Geller

=== More Recent Endeavors === Modeling two different classes of sculptures by Charles Perry and by Eva Hild.

“Tetra”, Waterfront Park, Louisville, KY Charles Perry, 1999, bronze Multiple views from the Web: Identify corresponding branches.

Modeling “Tetra” by Charles Perry (2) u Crude Assembling labeled ribbons Paper Models: Un-twisted tetrahedral frame Twisted tetra frame as in Perry’s “Tetra”

Modeling “Tetra” by Charles Perry (3) Annotated sculpture image Metal-rings Maquetteplus of scotch-tape model Perry’s “Tetra” CAD model of Perry’s “Tetra”

Modification of Perry’s “Tetra” Sculpture u Using my generator for tetrahedral ribbon frames, individually adjusting the twist of all six ribbons: Untwisted tetra frame – Emulating Perry’s “Tetra” and “D 2 d” 4 ribbons have a ± 360 twist

“Tetra_4 M” Modification of Perry’s Tetra Sculpture u The four twisted tetra-edges rotate through only 180. u 3 D-Print, painted This keeps the surface double-sided, but only 2 (different) borders. Original -- Modified u Double-sided (orientable) u Number of borders b = 2 u Euler characteristic χ = – 2 u Genus g = (2 – χ – b)/2 = 1 u It is a torus with 2 punctures.

“Tetra_6 M” Modification of Perry’s Tetra Sculpture u All SIX tetra-edges are twisted through 180. u This also makes it single-sided! u This one has 3 identical borders, forming a Borromean link !

2 -Manifold Sculptures “Wholly” by Eva Hild (Sweden)

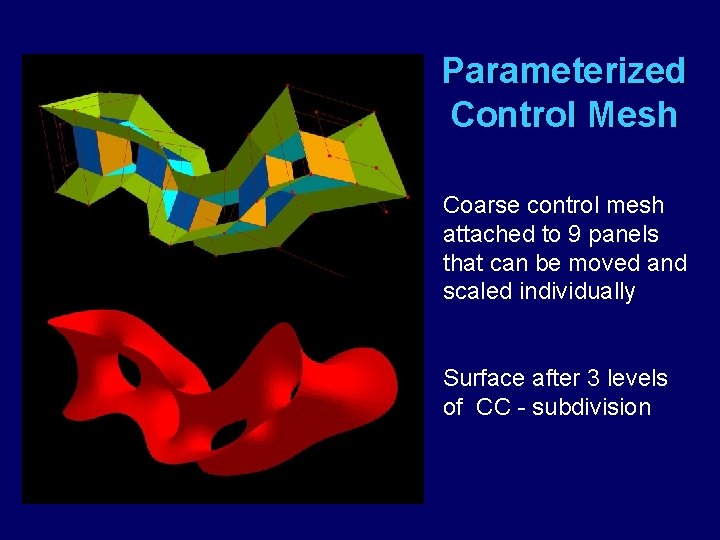
Parameterized Control Mesh Coarse control mesh attached to 9 panels that can be moved and scaled individually Surface after 3 levels of CC - subdivision

QUESTIONS ? ?

== SPARES ==

12 -Story Scherk-Collins Toroid u u u branches = 4 storeys = 11 height = 1. 55 flange = 1. 00 thickness = 0. 06 rim_bulge = 1. 00 warp = 330. 00 twist = 247. 50 azimuth = 56. 25 mesh_tiles = 0 textr_tiles = 1 detail = 8 u u u u bounding box: xmax= 6. 01, ymax= 1. 14, zmax= 5. 55, xmin= -7. 93, ymin= -1. 14, zmin= -8. 41

David Lynn, Nova Blue Studio Arts u http: //sites. google. com/site/novabluestudioarts/

Master Module for “Millennium Arch”

Fabrication of “Millennium Arch” The mold for the key module A polyester segment cast

Two Times Three Modules

Merging the Two Half-Circles

Brent Collins and David Lynn

“Millennium” Arch by Night