Visualizing HighOrder Surface Geometry Pushkar Joshi Carlo Squin

Visualizing High-Order Surface Geometry Pushkar Joshi, Carlo Séquin U. C. Berkeley

Clarification • This talk is NOT about a new CAD tool; but it describes a “Meta-CAD tool. ” • This talk is NOT about designing surfaces; it is about understanding smooth surfaces. This Presentation • Convey geometrical insights via a visualization tool for basic surface patches. • Give a thorough understanding of what effects higher-order terms can produce in smooth surfaces.

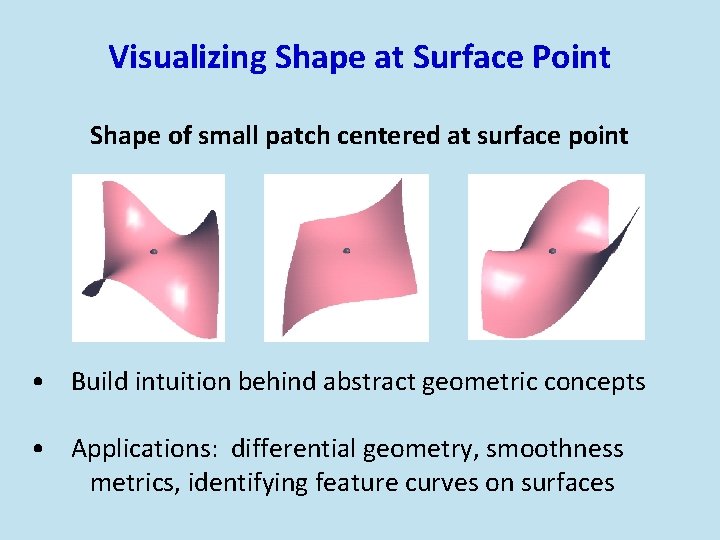
Visualizing Shape at Surface Point Shape of small patch centered at surface point • Build intuition behind abstract geometric concepts • Applications: differential geometry, smoothness metrics, identifying feature curves on surfaces

Minimizing Curvature Variation for Aesthetic Design Pushkar Joshi, Ph. D. thesis, Oct. 2008 Advisor: Prof. Carlo Séquin U. C. Berkeley http: //www. eecs. berkeley. edu/Pubs/Tech. Rpts/2008/EECS-2008 -129. html

Minimum Curvature Variation Curves, Networks, and Surfaces for Fair Free-Form Shape Design Henry P. Moreton, Ph. D. thesis, March 1993 Advisor: Prof. Carlo Séquin U. C. Berkeley http: //www. eecs. berkeley. edu/Pubs/Tech. Rpts/1993/5219. html

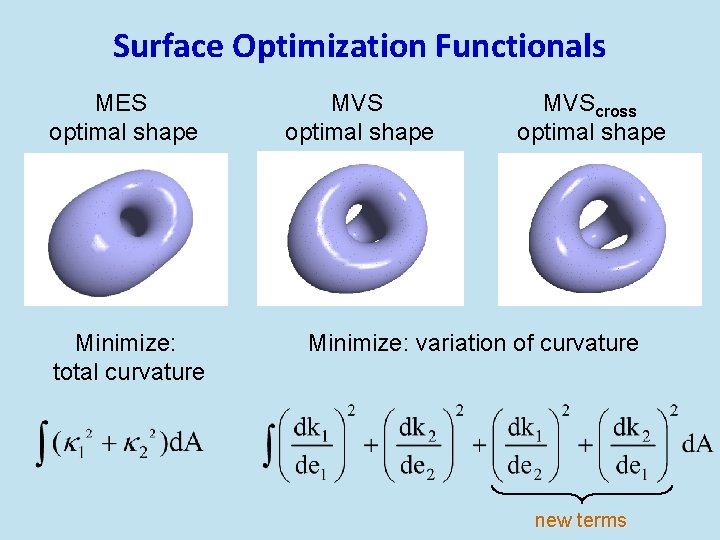
Surface Optimization Functionals MES optimal shape Minimize: total curvature MVS optimal shape MVScross optimal shape Minimize: variation of curvature new terms

Open Questions • What is the right way to measure “total curvature variation” ? – Should one average in-line normal curvature in all directions ? • How many independent 3 rd degree terms are there ? – Does MVScross capture all of them, – with the best weighting ? – Gravesen et al. list 18 different 3 rd-degree surface invariants ! • How do these functionals influence surface shapes ? – Which functional leads to the fairest, most pleasing shape ? • Which is best basis for capturing all desired effects ? – What is the geometrically simplest way to present that basis ? Draw inspiration from principal curvatures and directions, which succinctly describe second-degree behavior.

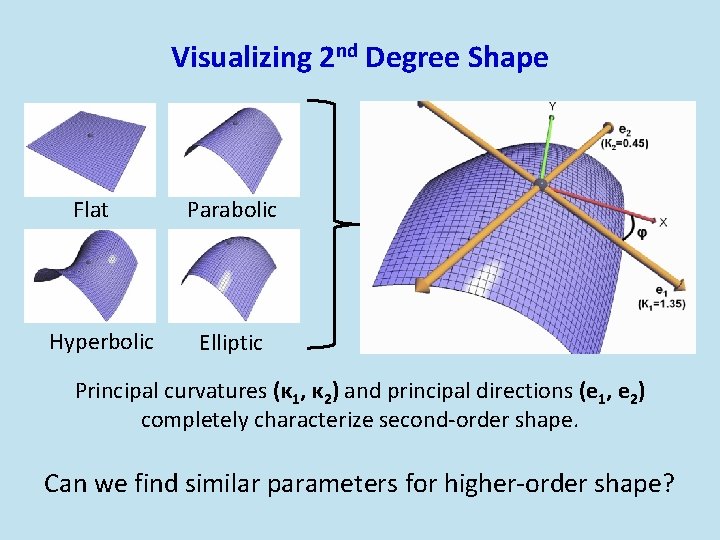
Visualizing 2 nd Degree Shape Flat Hyperbolic Parabolic Elliptic Principal curvatures (κ 1, κ 2) and principal directions (e 1, e 2) completely characterize second-order shape. Can we find similar parameters for higher-order shape?

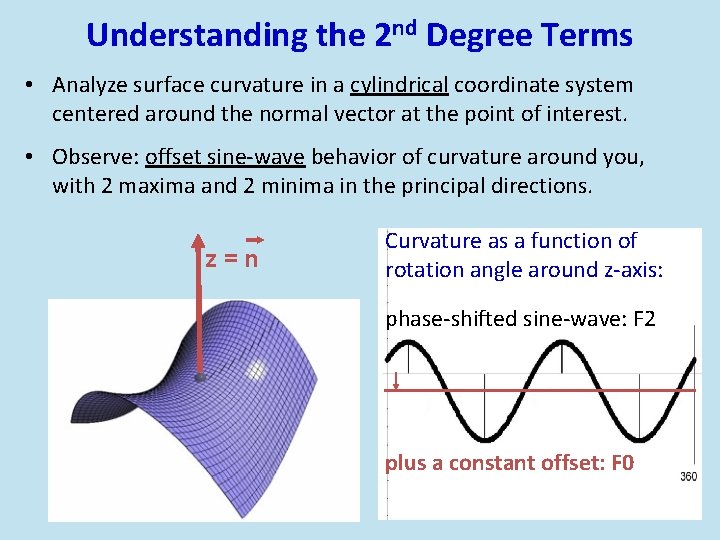
Understanding the 2 nd Degree Terms • Analyze surface curvature in a cylindrical coordinate system centered around the normal vector at the point of interest. • Observe: offset sine-wave behavior of curvature around you, with 2 maxima and 2 minima in the principal directions. z=n Curvature as a function of rotation angle around z-axis: phase-shifted sine-wave: F 2 plus a constant offset: F 0

Polynomial Surface Patch z(u, v) = C 0 u 3 + C 1 u 2 v + C 2 uv 2 + C 3 v 3 4 Parameters! + Q 0 u 2 + Q 1 uv + Q 2 v 2 + L 0 u + L 1 v + (const. ) Ignore (for now)

Fourier Analysis of Height Field zc(r, θ) = r 3 [ C 0 cos 3(θ)+ C 1 cos 2(θ)sin(θ)+ C 2 cos(θ)sin 2(θ)+ C 3 sin 3(θ)] zc(r, θ) = r 3 [ F 1 cos( θ + α ) + F 3 cos(3( θ + α + β )) ] + = zc(θ) F 1 cos(θ+α) F 3 cos(3(θ+α+β))

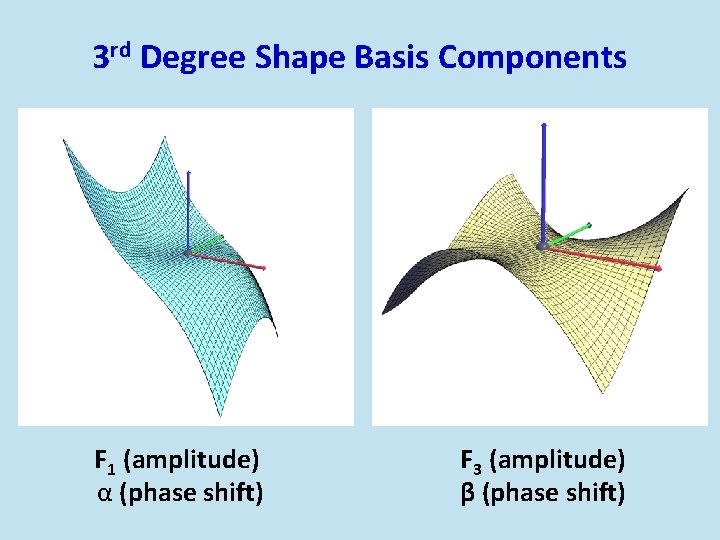
3 rd Degree Shape Basis Components F 1 (amplitude) α (phase shift) F 3 (amplitude) β (phase shift)

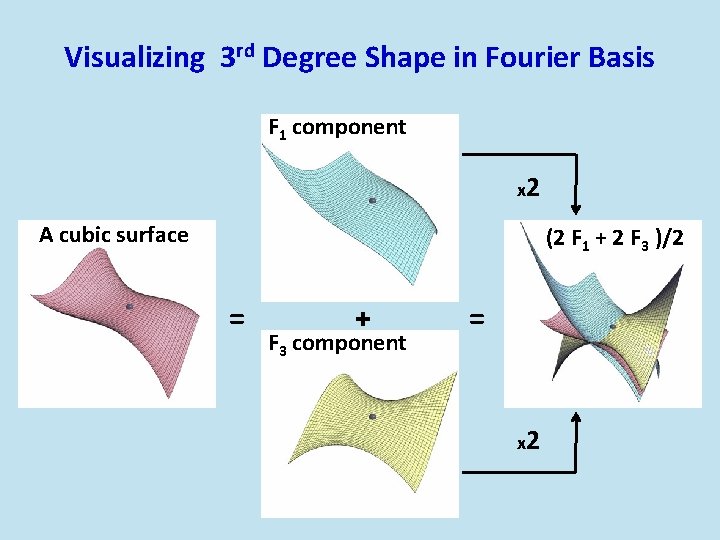
Visualizing 3 rd Degree Shape in Fourier Basis F 1 component x 2 A cubic surface (2 F 1 + 2 F 3 )/2 = + F 3 component = x 2

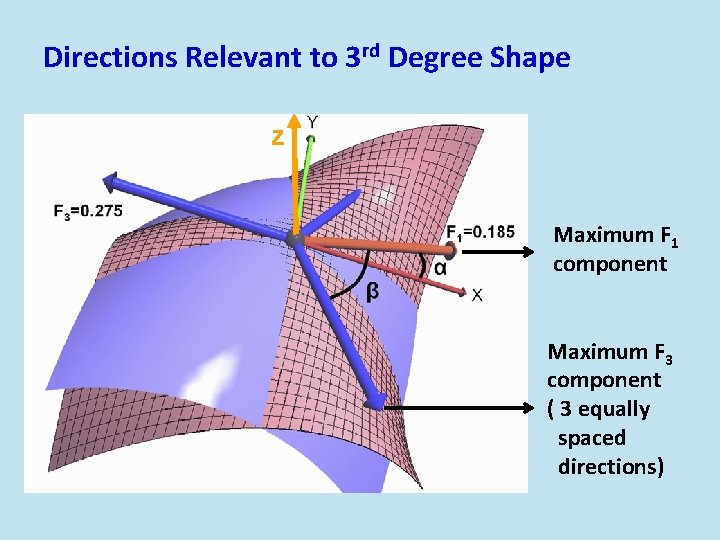
Directions Relevant to 3 rd Degree Shape z Maximum F 1 component Maximum F 3 component ( 3 equally spaced directions)

GUI of the Visualization Tool Polynomial Coefficients Surface near point of analysis Fourier Coefficients Surface is modified by changing polynomial coefficients or Fourier coefficients. Changing one set of coefficients automatically changes the other set.

Polynomial & Fourier Coefficients z(r, θ) = r 3 [ J cos 3θ + I sin 3θ + H cos 2θ sinθ + G cosθ sin 2θ ] + r 2 [ F cos 2θ + E sin 2θ + D cosθ sinθ ] + r [ C cosθ + B sinθ ] + A (equivalent) z(r, θ) = r 3 [ F 3_1 cos(θ + α) + F 3_3 cos 3(θ + α + β) ] + r 2 [ F 2_0 + F 2_2 cos 2(θ + γ) ] + r [ F 1_1 cos(θ + δ) ] + For the math see: F 0_0 Joshi’s Ph. D thesis

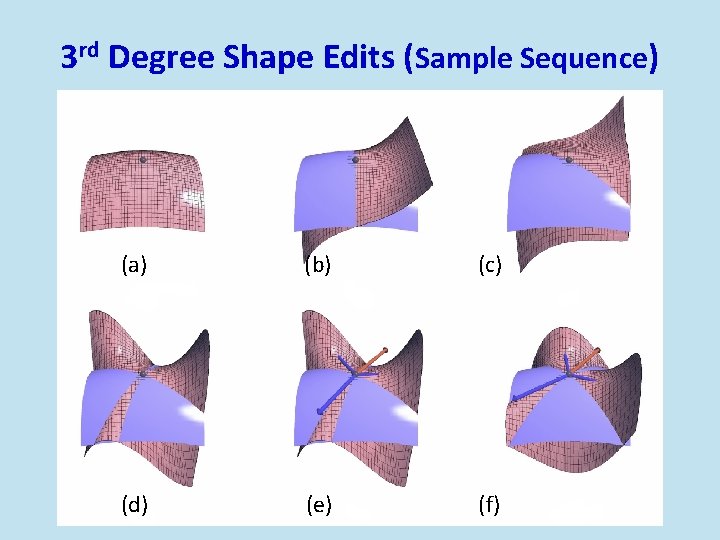
3 rd Degree Shape Edits (Sample Sequence) (a) (b) (c) (d) (e) (f)

Visualizing the Properties of a Surface Patch Quadratic overlaid on cubic

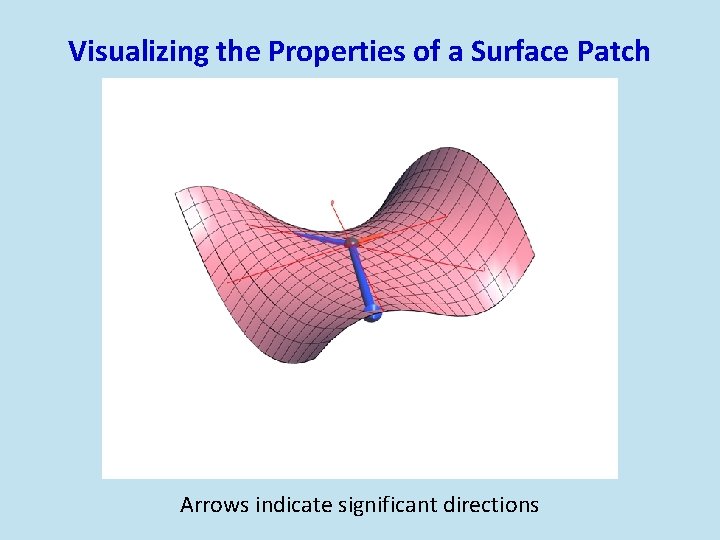
Visualizing the Properties of a Surface Patch Arrows indicate significant directions

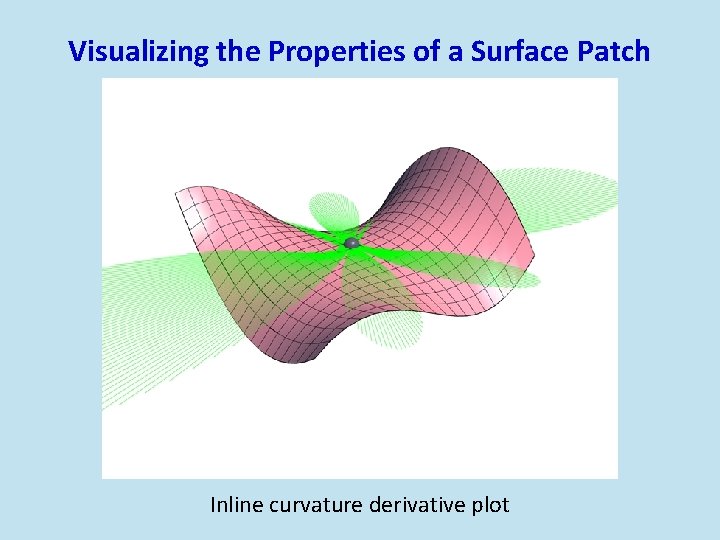
Visualizing the Properties of a Surface Patch Inline curvature derivative plot

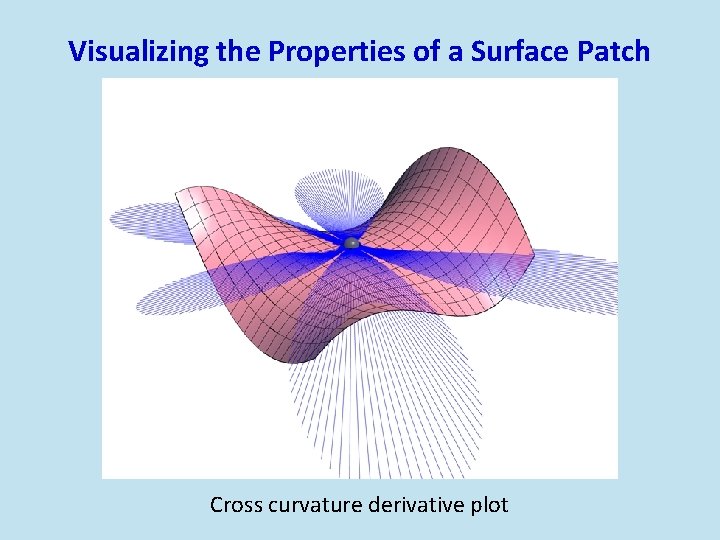
Visualizing the Properties of a Surface Patch Cross curvature derivative plot

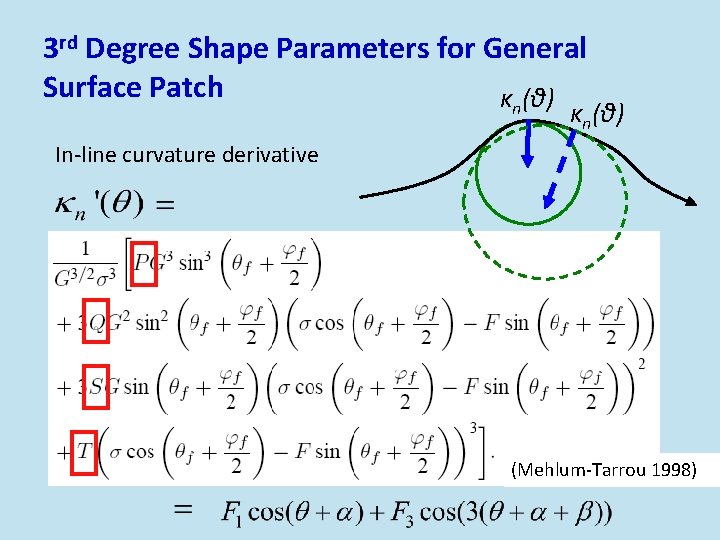
3 rd Degree Shape Parameters for General Surface Patch κ (θ) n κn(θ) In-line curvature derivative (Mehlum-Tarrou 1998)

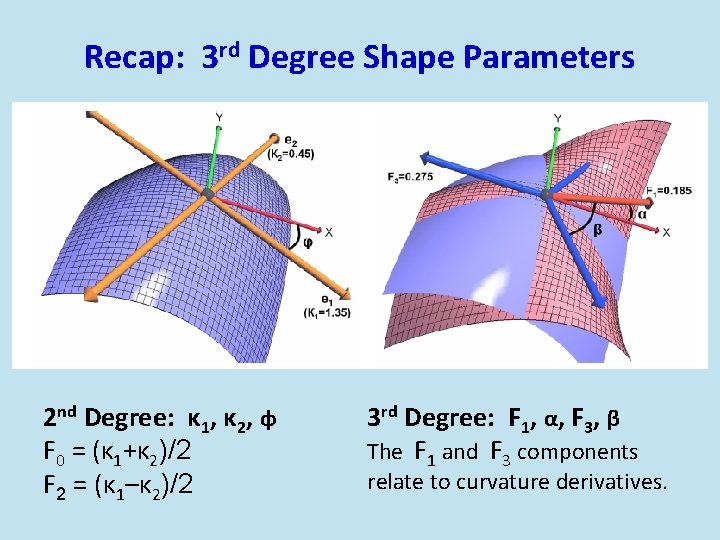
Recap: 3 rd Degree Shape Parameters 2 nd Degree: κ 1, κ 2, φ F 0 = (κ 1+κ 2)/2 F 2 = (κ 1–κ 2)/2 3 rd Degree: F 1, α, F 3, β The F 1 and F 3 components relate to curvature derivatives.

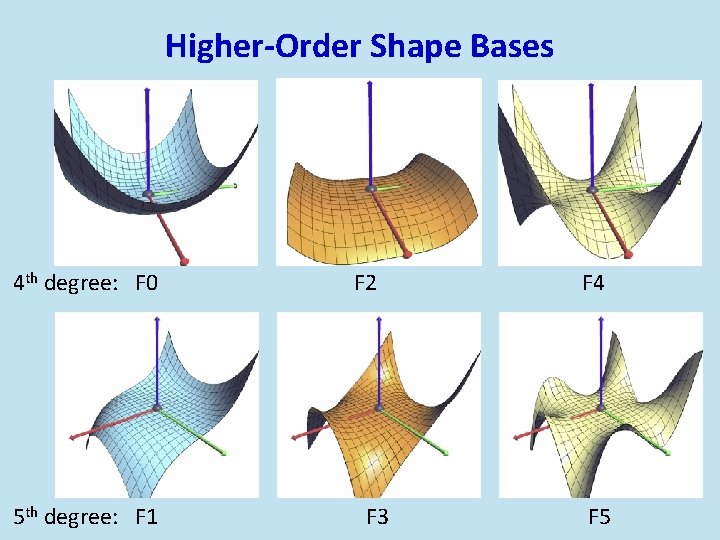
Higher-Order Shape Bases 4 th degree: F 0 5 th degree: F 1 F 2 F 3 F 4 F 5

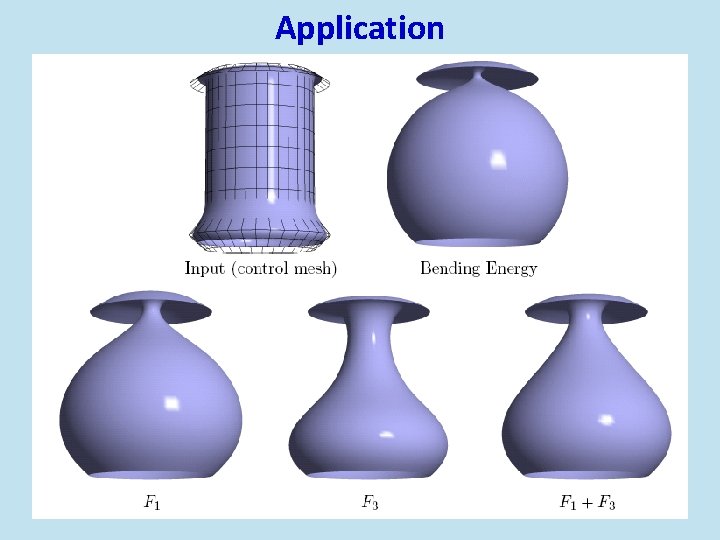
Application

Summary Visualize 3 rd degree basis shapes (using polynomial height field) Develop theory of high-order basis shapes (Fourier coefficients) Visualize higher-order (4 th degree and 5 th degree) basis shapes