Cryptography Where Complexity Finally Comes In Handy Complexity

Cryptography Where Complexity Finally Comes In Handy… Complexity ©D. Moshk 1

The Amazing Adventures of Alice and Bob extremely secret message Alice Bob eavesdropper Complexity ©D. Moshk 2

PAP 279 -298 Introduction • Objectives: – To introduce the subject of cryptography and its tight connection to complexity • Overview: – Public key cryptography – One-Way Functions and Trapdoor functions – RSA Complexity ©D. Moshk 3

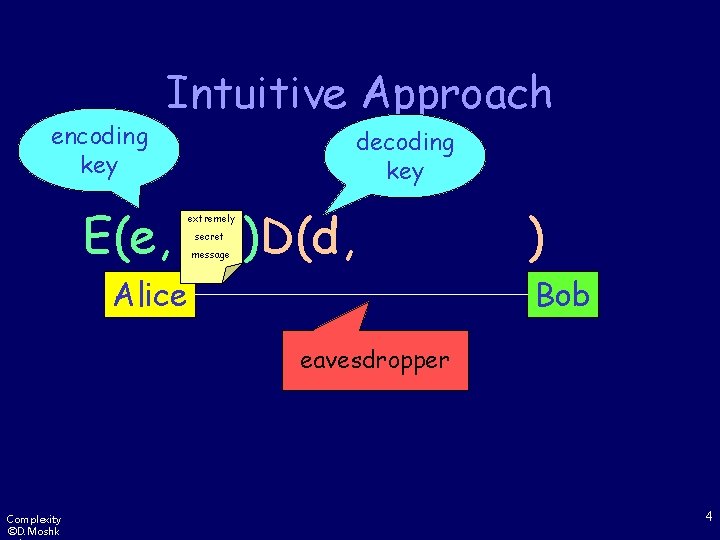
encoding key Intuitive Approach E(e, decoding key extremely secret message )D(d, Alice ) Bob eavesdropper Complexity ©D. Moshk 4

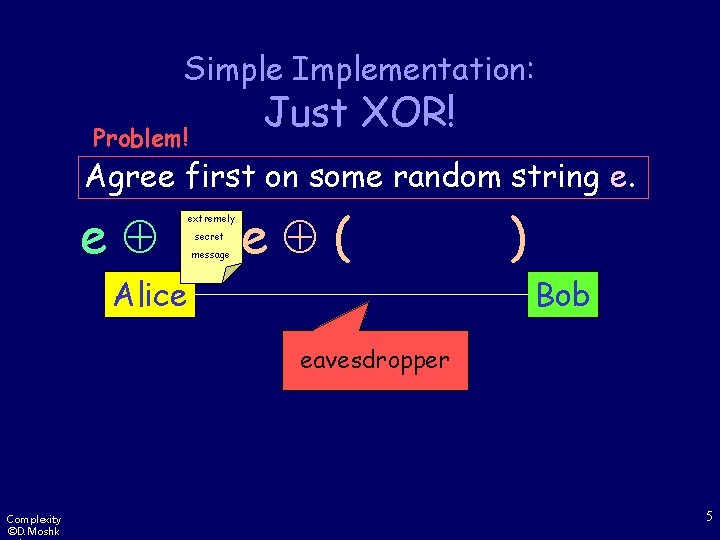
Simple Implementation: Just XOR! Problem! Agree first on some random string e. e extremely secret message e ( Alice ) Bob eavesdropper Complexity ©D. Moshk 5

Solution: Public-Key Cryptosystems • Bob generates a pair of keys • Publishes E • Keeps D private E(x) Bob D(y) Complexity ©D. Moshk 6

Encryption: Requirements • “Easy” (so everyone can send Bob encrypted messages) • “Hard to invert” (so no one can break the encryption) Complexity ©D. Moshk 7

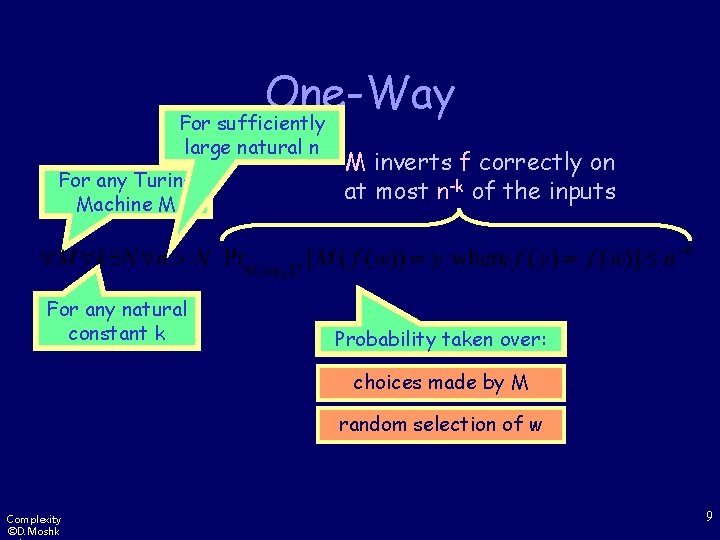
SIP 375 One-Way Functions: Formally Definition: A length preserving function f is a oneway function if: some 1. f is computable in polynomial time. textbooks 2. f-1 cannot be computed in probabilistic demand f is one-to-one polynomial time, i. e Complexity ©D. Moshk 8

One-Way For sufficiently large natural n For any Turing Machine M For any natural constant k M inverts f correctly on at most n-k of the inputs Probability taken over: choices made by M random selection of w Complexity ©D. Moshk 9

Applications: Authentication • Many users may login to a network • Each user has a password • The database can be read by everyone • Problem: secure authentication Complexity ©D. Moshk 10

How to Authenticate Using OWF? One-Way Function • Encrypt each password with a OWF. • Store only the encrypted password. • When this user tries to login… – Encrypt the password she entered – Compare to the stored password Complexity ©D. Moshk My. Pass 1234 2 i. B>S]1%^o 11

Do One-Way Functions Exist? • Believed to… • OWF P≠NP. Complexity ©D. Moshk 12

Do One-Way Functions Suffice? Problem: How would Bob generate D(y)? D is so hard, I don’t know how to compute it myself… Bob Complexity ©D. Moshk 13

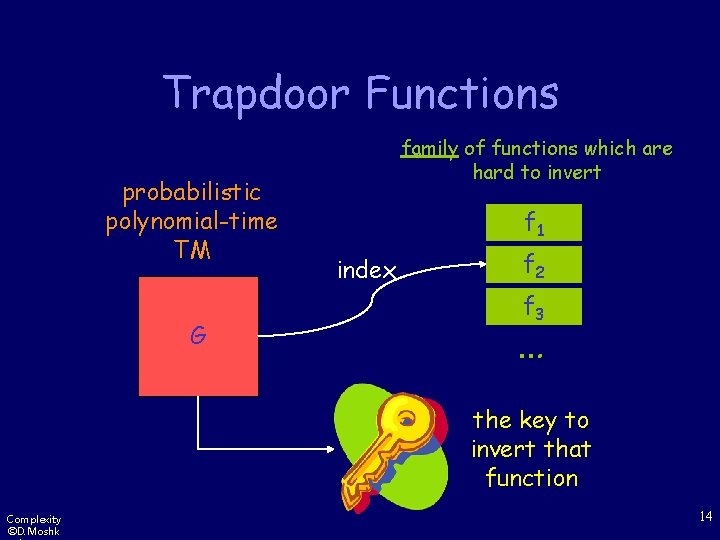
Trapdoor Functions probabilistic polynomial-time TM G family of functions which are hard to invert f 1 index f 2 f 3 … the key to invert that function Complexity ©D. Moshk 14

SIP 376 -377 Trapdoor Functions : Formally Definition: A length preserving indexing function f: * * * is a trapdoor function, if there exist f(i, w)=fi(w) <index, key> generator • a poly-time TM G • a function h: * * * which satisfy: decoder Complexity ©D. Moshk 15

SIP 376 -377 Trapdoor Functions : Formally 1. f and h are computable in polynomial time. 2. “fi is hard to invert in the absence of t” <i, t> is output by G 3. “fi is easy to invert when t is known” Complexity ©D. Moshk 16

RSA • A public-key cryptosystem developed by Rivest, Shamir and Adleman. • Based on the (conjectured) hardness of factoring. Complexity ©D. Moshk 17

Plan 1. Prime numbers: basic facts and recent results. 2. Euler’s function. 3. Description of the RSA cryptosystem. Complexity ©D. Moshk 18

PRIMES • Instance: A number in binary representation. • Problem: To decide if this number is prime. Complexity ©D. Moshk Yes instance: 10111 No instance: 10110 19

Is PRIMES in P ? ! What’s the problem with the following trivial algorithm? Input: a number N Output: is N prime? for i in 2. . N do for j in 2. . N do if i*j=N, return FALSE return TRUE Complexity ©D. Moshk 20

Prime Numbers • Fact 1: There are many prime numbers (k/log k in the range [k]={1, …, k}) • Fact 2: ([AKS 02]) Primality testing can be done in time polynomial in log k. • Question: How to choose a random prime in [k] in time poly-log k? Complexity ©D. Moshk 21

Picking a Random Prime • while didn’t-find-one uniformly at random – choose x R [k] – if x PRIMES [k] • return x Expected time: O(polylogk) Complexity ©D. Moshk primes 22

De-Randomization • By Alon et Al and Naor, there’s a deterministic construction X of O(logk/ 2) numbers in [k] which is -close to uniform. If Prx R[k] [x S] > X S≠ • By using it with < log-1 k, we can obtain O(polylogk) run-time (not just expectedly!) Complexity ©D. Moshk 23

Euler’s Function • (n) = { m | 1 m < n AND gcd(m, n)=1 } • Euler’s function: (n)=| (n)| Example: (12)={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} (12)=4 Observe: For any prime p, (p)={1, . . . , p-1} Complexity ©D. Moshk 24

RSA • To encrypt a message, write it as a number m, and compute EN, e(m) = me (mod N) • To decrypt a cipher text c, compute Dd(c) = cd (mod N) • Now for (almost) any m, – med m (mod N) – And therefore: (me)d m (mod N) Therefore: Dd(EN, e(m)) m Complexity ©D. Moshk (mod N) 25

The Public and Private Keys • Choose two long random prime numbers p, q – set N = pq • Randomly choose an odd number e s. t: – 1 < e < (N) Compute d using Euclid’s – gcd(e, (N)) = 1 • Let d be the inverse of e, namely gcd algorithm ed 1 (mod (n)) Public key: <N, e> Complexity ©D. Moshk ; Private key: d 26

Summary • We presented the notion of Public Key Cryptosystems and its well-known implementation, RSA. • We examined some of the underlying assumptions of cryptography: – Existence of one-way functions – Existence of trapdoor functions • These assumptions are stronger than the standard complexity assumption P≠NP. Complexity ©D. Moshk 27