Cours analyse spectrale Part I ESPEO 3me anne

Cours analyse spectrale Part I ESPEO 3ème année Philippe Ravier 2000 -2001

Déroulement du cours 1. 2. 3. 4. Définitions : spectre, dsp, corrélation Procédure d’estimation Estimation de la fonction de corrélation Mesure de fonctions de corrélation par TFD

1. Définitions : spectre, dsp, corrélation Ø On définit : - le spectre d’amplitude - le spectre de phase - on parle de spectre de raies pour le spectre d’un signal constitué de fréquences pures Ø La dsp est définie à partir de la fonction d’autocorrélation comme Théo. de Wiener-Kintchine

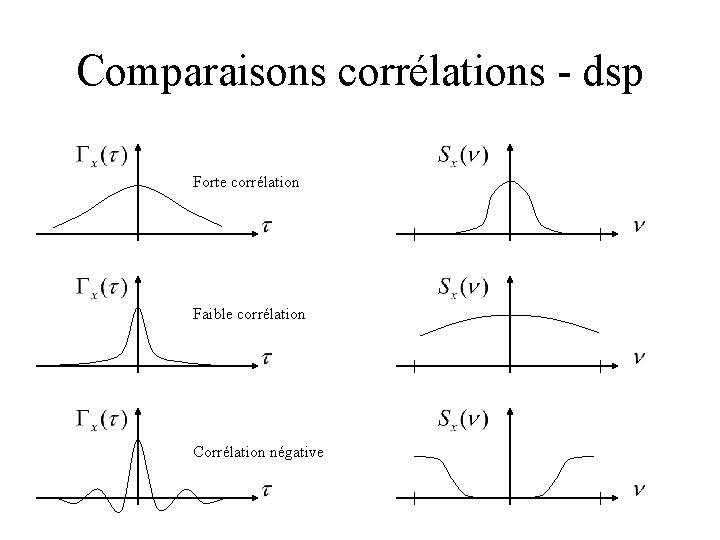
Comparaisons corrélations - dsp Forte corrélation Faible corrélation Corrélation négative

Corrélation, dse et dsp (cas certain) Ø signal déterministe ou certain • signal à énergie finie dse • signal à puissance moyenne finie dsp • signal périodique (T) : cas particulier du signal à puissance moy. finie dsp

Corrélation, dse et dsp (cas aléatoire) Ø signal aléatoire centré Comment calculer la dsp avec une espérance mathématique ? Si le processus aléatoire est stationnaire et ergodique, alors : dont on prend la TF Corrélogramme Si le signal est stationnaire et ergodique, on peut remplacer E par un moyennage sur plusieurs réalisations indépendantes. On ne dispose que d’une réalisation. On va envisager plusieurs réalisations d’un même processus par tronçonnage de ce processus. Périodogramme moyenné

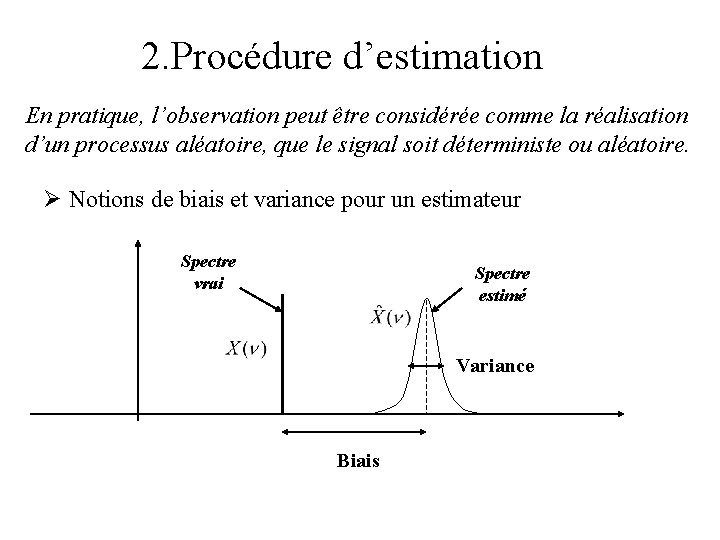
2. Procédure d’estimation En pratique, l’observation peut être considérée comme la réalisation d’un processus aléatoire, que le signal soit déterministe ou aléatoire. Ø Notions de biais et variance pour un estimateur Spectre vrai Spectre estimé Variance Biais

Formulations mathématiques des statistiques de l’estimateur estimé à partir des observations Y Biais (moment du 1 er ordre) Variance (moment du 2ème ordre) Erreur entre la grandeur réelle et l’estimée

• Si l’estimateur est dit non biaisé • On a une borne inférieure de la variance : Borne de Cramér-Rao pour un estimateur sans biais • Si la variance atteint la borne de CR, on dit que l’estimateur est efficace L’estimateur idéal est non biaisé et efficace mais variance et biais sont liés par l’EQM Antagonisme biais-variance • L’estimateur est dit consistent si le biais et la variance tendent vers 0 quand le nombre d’observations tend vers l’infini

Exemple avec l’estimateur de la moyenne Signal aléatoire X(n) Stationnaire et ergodique Durée limitée de N points Moyenne estimée Variable aléatoire sur l’ensemble des réalisations de X(n) On trouve (éch. indép. de var s 2)

Exemple avec l’estimateur de la corrélation Estimateur « naturel » pour un nombre N de points Est-ce un bon estimateur ? Cet estimateur est biaisé car on ne tient pas compte de la durée finie des signaux. Pour « rendre » le signal à énergie finie, on utilise des fonctions de pondération qui atténuent les extrémités. Estimateur non biaisé

3. Estimation de la fonction de corrélation On multiplie le signal temporel par une fonction d’apodisation (pondération ou lissage) g(t) Forme générale de la fonction d’apodisation g(t) 0 T Rôle : • atténue les discontinuités qui apparaissent aux 2 extrémités du signal observé • permet de régler le biais de l’estimateur • intervient sur la variance de l’estimateur La fonction d’auto-corrélation est alors estimée par

Ø Moyenne de l’estimateur Fonction de corrélation de g(t) : Pour obtenir un estimateur non biaisé, il suffit de fixer : Estimateur approximativement non biaisé Ø Variance de l’estimateur Expression approchée pour le cas gaussien et un support de fonction de corrélation petit par rapport à la durée d’observation, soit t<<T

Introduisons quelques grandeurs - On définit le temps d’intégration C’est une mesure de la durée de g(t) qui est le temps d’observation sur lequel on effectue l’estimation. - On définit la largeur de bande équivalente de bruit C’est une mesure de la largeur de bande de x(t). Elle est définie à partir de la bande équivalente d’un bruit associé à x(t).

- On définit le temps de corrélation C’est une mesure de la durée de la fonction de corrélation Variance relative à la puissance de l’estimateur avec ces notations dépend de la fonction de corrélations de x(t)

La variance est essentiellement contrôlée par le produit Beq. Tin • Pour avoir une variance faible, il faut prendre un temps d’intégration le plus grand possible, bien plus grand que le temps de corrélation du signal. • Autre interprétation : Tin / Tc correspond au nombre de supports de la fonction de corrélation contenus dans la durée du signal observé. C’est le nombre de tranches indépendantes (décorrélées) du signal utilisées pour faire l’estimation. Variance relative (pour un retard quelconque) La dispersion relative des estimations augmente pour les retards importants. L’estimation est moins bonne pour les t grands.

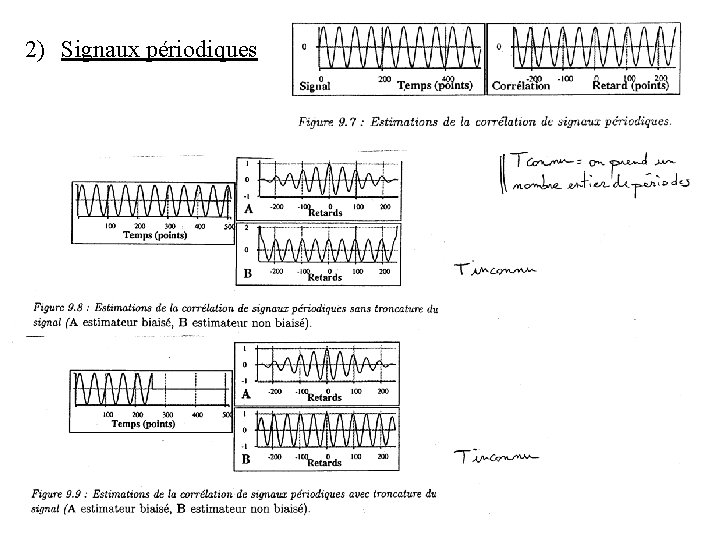
4. Mesure de fcts de corrélation par TFD L’estimation par la TFD introduit une estimation de la corrélation circulaire. La notation [n-k] signifie : [n-k] = n-k modulo N 1) Signaux à énergie finie Forme incorrecte venant du repliement induit par la translation circulaire

2) Signaux périodiques

3) Signaux aléatoires L’estimateur est une variable aléatoire qui a un biais et une variance. Même variance que dans le cas continu est la longueur du support de corrélation en nombre d’échantillons. Bilan : - signaux à énergie finie : ajout de zéros pour calcul par TFD - signaux périodiques : estimation erronée sauf si on connaît la période - signaux aléatoires stationnaires : estimation correcte si le calcul est effectué sur une durée supérieure au temps de corrélation. La variance relative croît pour les retards forts.