Cortes cutsets UFES Corte por arestas Em um


























- Slides: 31

Cortes (cut-sets) UFES

Corte por arestas • Em um grafo conexo G, um corte de arestas é um conjunto de arestas cuja remoção de G torna G desconexo, desde que nenhum subconjunto próprio desse conjunto também desconecte G Teoria dos Grafos (INF 5037) UFES

Corte por arestas • rank de um grafo: r = n - (G) • Subconjunto minimal de arestas de maneira a garantir a conexidade de cada componente do grafo • corte de arestas: subconjunto minimal de arestas cuja remoção reduz o rank de um grafo de uma unidade. Teoria dos Grafos (INF 5037) UFES

Corte por arestas • corte de arestas: subconjunto minimal de arestas cuja remoção acarreta uma partição no grafo. Teoria dos Grafos (INF 5037) UFES

Propriedades • Todo corte de arestas de um grafo conexo G deve conter pelo menos uma aresta de toda árvore geradora de G; • Em um grafo conexo G, qualquer conjunto minimal de arestas contendo pelo menos uma aresta de qualquer árvore geradora de G é um corte de arestas; • Todo ciclo possui um número par de arestas em comum com qualquer corte de arestas Teoria dos Grafos (INF 5037) UFES

Corte por Aresta (Bondy & Murty) • Para subconjuntos S e S’ de V, denotamos por [S, S´] o conjunto de arestas com um extremo em S e outro em S´ Teoria dos Grafos (INF 5037) UFES

Corte por Aresta (Bondy & Murty) • Para subconjuntos S e S’ de V, denotamos por [S, S´] o conjunto de arestas com um extremo em S e outro em S´ • Seja C um subconjunto de E da forma [S, S´], onde S é um subconjunto não vazio e próprio de V e S´=V-S Teoria dos Grafos (INF 5037) UFES

Bond • Se C é minimal, então C é um corte de arestas de G. • Em alguns livros o corte de arestas é denominado bond. • Se G é conexo, então um bond B de G é um subconjunto minimal de E tal que G-B é desconexo. Teoria dos Grafos (INF 5037) UFES

Exemplo: G Teoria dos Grafos (INF 5037) UFES

Exemplo: G a b Teoria dos Grafos (INF 5037) UFES

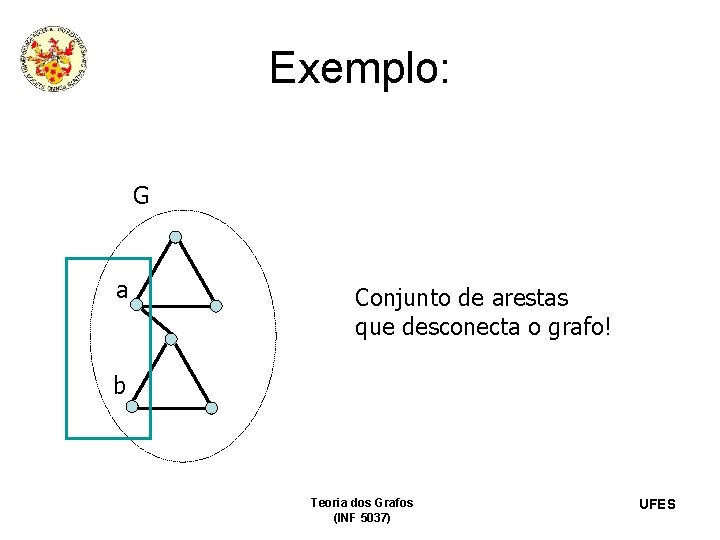
Exemplo: G a Conjunto de arestas que desconecta o grafo! b Teoria dos Grafos (INF 5037) UFES

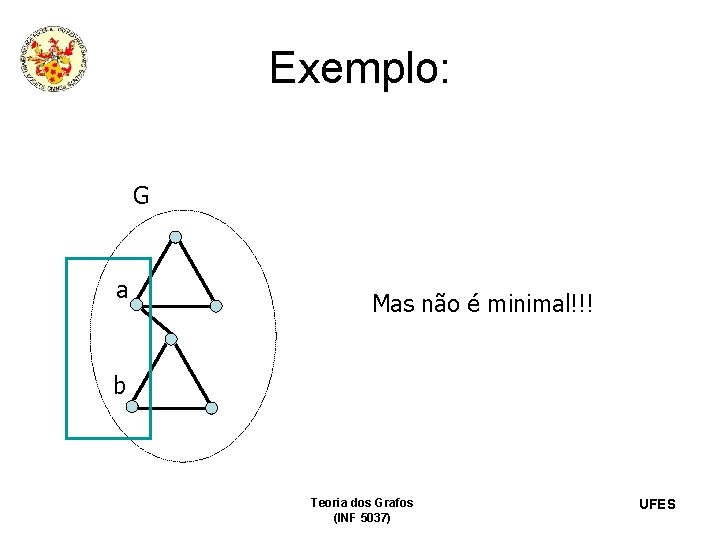
Exemplo: G a Mas não é minimal!!! b Teoria dos Grafos (INF 5037) UFES

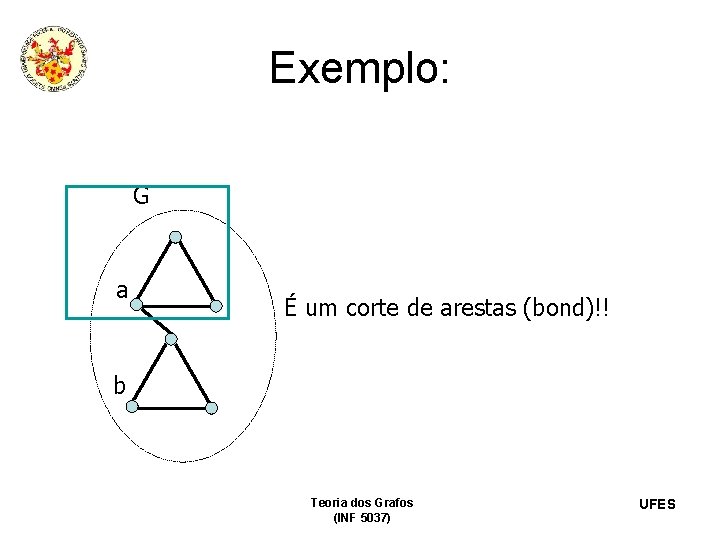
Exemplo: G a É um corte de arestas (bond)!! b Teoria dos Grafos (INF 5037) UFES

Cotree • Se H é um subgrafo de G, o complemento de H em G, denotado por H é o subgrafo G-E(H). • Se G é conexo, e T é uma árvore geradora de G, então T é dita cotree de G Teoria dos Grafos (INF 5037) UFES

Teorema: Seja T uma árvore geradora de um grafo conexo G e seja a uma aresta de T. Então: a) a cotree T não contém corte de aresta de G; b) T + a contem um único corte de arestas de G. Teoria dos Grafos (INF 5037) UFES

Prova • Exercício!!!!! Teoria dos Grafos (INF 5037) UFES

Conectividade e Separabilidade Teoria dos Grafos (INF 5037) UFES

Conectividade de arestas • Em um grafo conexo G, o número de arestas do menor corte de arestas de G é definido como conectividade de arestas de G (K´ (G)) • K´ (G): número mínimo de arestas cuja remoção reduz o rank de G em uma unidade. • K´(T) = ? ? , onde T é uma árvore. Teoria dos Grafos (INF 5037) UFES

Corte de vértices • Subconjunto minimal de vértices V´ V, cuja remoção de G o desconecta ou o transforma em um grafo nulo. • G – V´: desconexo ou nulo e subconjunto próprio V´´ V´, G – V´´ é conexo e não nulo. Teoria dos Grafos (INF 5037) UFES

Conectividade de vértices • O número mínimo de vértices que desconecta o grafo G ou o reduz a um único vértice é definido como conectividade de vértices de G (K (G)) • K(T) = ? ? , onde T é uma árvore. • Conectividade de vértices tem sentido apenas para grafos conexos com mais de três vértices e não completos. Teoria dos Grafos (INF 5037) UFES

Conectividade de vértices • K´(G) = K(G) = 0, G desconexo • K(G) n – 2, G Kn Teoria dos Grafos (INF 5037) UFES

Grafo separável • Um grafo G é dito separável quando K(G) = 1. • Neste caso, G pode ser decomposto em subgrafos G 1 e G 2 tal que G 1 e G 2 tem apenas um vértice em comum. Teoria dos Grafos (INF 5037) UFES

Articulação • Vértice cuja remoção desconecta o grafo. Teoria dos Grafos (INF 5037) UFES

Teorema Seja G (V, E) um grafo conexo, |V| > 2. Então: a) Um vértice v de V é articulação sss existem dois vértices x e y em G, x, y v, tais que todo caminho entre x e y passa por v; b) Uma aresta {p, q} de E é ponte sss {p, q} for o único caminho entre p e q em G. Teoria dos Grafos (INF 5037) UFES

Exemplo Suponha que são dadas n estações que devem ser conectadas por e linhas, e ≥ n-1. Qual é a melhor maneira de conectá -las, de maneira a evitar sua destruição devido à destruição de estações individuais e/ou linhas individuais? Maior conectividade de vértices e arestas Teoria dos Grafos (INF 5037) UFES

Teorema A conectividade de arestas de um grafo G não pode exceder o grau do vértice com o menor grau de G Teoria dos Grafos (INF 5037) UFES

Prova • Seja w o vértice de grau mínimo de G ( ) • É possível desconectar G, removendo-se as arestas incidentes a w. • ≥ K´(G) Teoria dos Grafos (INF 5037) UFES

Teorema A conectividade de vértices de um grafo G não pode exceder a conectividade de arestas de G Teoria dos Grafos (INF 5037) UFES

Questão Sejam G = (V, E) um grafo e E´ um corte de arestas de G. É sempre possível encontrar um corte de vértices V´ tal que |V´| |E´|? Teoria dos Grafos (INF 5037) UFES

G, K(G) K´(G) Teoria dos Grafos (INF 5037) UFES

Corolário Todo corte de arestas em um grafo não separável com mais de dois vértices contém pelo menos duas arestas Teoria dos Grafos (INF 5037) UFES
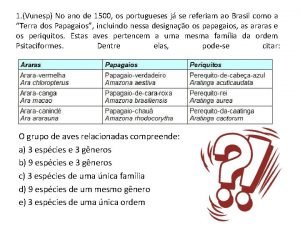
 Vunesp sp no ano de 1500 os portugueses
Vunesp sp no ano de 1500 os portugueses Ufes abb
Ufes abb Cortes y secciones
Cortes y secciones Herramientas de corte por aserrado
Herramientas de corte por aserrado Sólido geométrico
Sólido geométrico Quantos vértices tem uma pirâmide de base triangular
Quantos vértices tem uma pirâmide de base triangular Circulo é um poliedro
Circulo é um poliedro Prisma solido
Prisma solido O que são segmentos de reta perpendiculares
O que são segmentos de reta perpendiculares Planificação retangulo
Planificação retangulo Paralelepípedo quadrangular
Paralelepípedo quadrangular Poliedro com 5 faces 6 vertices e 9 arestas
Poliedro com 5 faces 6 vertices e 9 arestas Face aresta e vertice
Face aresta e vertice Poliedro convexo
Poliedro convexo Faces laterais
Faces laterais Prisma hexagonal quantas faces arestas e vertices
Prisma hexagonal quantas faces arestas e vertices Pirâmide de base quadrada faces vértices e arestas
Pirâmide de base quadrada faces vértices e arestas Cortes villa savoye
Cortes villa savoye Hannah herman cortes
Hannah herman cortes Las cortes de cadiz
Las cortes de cadiz Hernan cortes travel map
Hernan cortes travel map Cortes de organos
Cortes de organos John cabot sponsoring country
John cabot sponsoring country Color in motion maria claudia cortes
Color in motion maria claudia cortes Hannah hernan cortes
Hannah hernan cortes Rico cortes wisdom in torah
Rico cortes wisdom in torah Cortes de la esfera
Cortes de la esfera Gineclogo
Gineclogo Cortes cerebrales
Cortes cerebrales Jesus julian cortes vela
Jesus julian cortes vela Corinna cortes
Corinna cortes Hernando cortes voyage route
Hernando cortes voyage route