Coordinacin de Ciencias Computacionales INAOE Matemticas Discretas Mini

Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas (Mini) Cursos Propedéuticos 2012 Ciencias Computacionales INAOE Dr. Hugo Jair Escalante hugojair@inaoep. mx http: //ccc. inaoep. mx/~hugojair Oficina 8319 Este material se basa en versiones previas del mismo por: Dr. Enrique Muñoz de Cote Dr. Enrique Sucar Dr. Luis Villaseñor

SEGUNDA PARTE Conteo 1. • • • Introducción Reglas de la suma y el producto Permutaciones Combinaciones Generación de permutaciones Teorema del Binomio

Introducción � Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar. � Ejemplo : ¿Cuántas maneras tiene una persona de seleccionar una lavadora, una batidora y dos licuadoras, si encuentra en una tienda 8 modelos diferentes de lavadoras, 5 modelos diferentes de batidoras y 7 modelos diferentes de licuadoras? . � Se les denomina técnicas de conteo a las: • combinaciones, • permutaciones y • diagrama de árbol � Las bases para entender el uso de las técnicas de conteo son el principio multiplicativo y el aditivo. 3

Introducción � En ocasiones, interesa saber cuántas diferentes permutaciones/combinaciones de elementos se pueden generar a partir de cierto conjunto, por ejemplo: • Cuántos comités diferentes de 3 personas puede haber a partir de un grupo de 10 individuos? • De cuántas diferentes maneras pueden repartirse 5 cartas a partir de 52 cartas (poker)? 4

Introducción � En la mayoría de los problemas de análisis combinatorio se observa que una operación o actividad aparece en forma repetitiva y es necesario conocer las formas o maneras que se puede realizar dicha operación. � Para dichos casos es útil conocer determinadas técnicas o estrategias de conteo que facilitarán el calculo señalado. � En esta sesión veremos la teoría matemática que nos permite hacer éstos cálculos, así como algunos ejemplos de aplicación 5

Experimento � Un proceso físico que tiene un número de posibles resultados � Ejemplos: • Tirar una moneda y observar que cara queda arriba • Tirar n monedas y observar las caras quedan arriba en cada moneda • Sacar m pelotas de una caja con n pelotas • Seleccionar 3 miembros para un comité de un grupo de n personas • De n personas que fuman, observar cuántas tienen cáncer 6

Principio de adición Supongamos que un evento A se puede realizar de m maneras y otro evento B se puede realizar de n maneras diferentes, además, no es posible que ambos eventos se realicen juntos, entonces el evento A o el evento B se puede realizar de (m + n) maneras.

Ejemplo : Un repuesto de automóvil se venden en 6 tiendas en Morelia o en 8 tiendas de Cuernavaca. ¿De cuántas formas se puede adquirir el repuesto? Solución : Por el principio de adición: Morelia ó Cuernavaca 6 formas + 8 formas = 14 formas

Principio de adición � Si hacemos 2 experimentos, uno con n posibles resultados, y otro con m posibles resultados, el número total de resultados al realizar exactamente uno de los experimentos es m + n � Ejemplos: • A partir de 10 senadores y 10 diputados se va a hacer un comité con 3 miembros, todos ellos diputados o senadores, de cuántas formas se puede conformar el comité? 9

Principio De Multiplicación Si un evento o suceso A puede ocurrir, en forma independiente, de m maneras diferentes y otro suceso B de n maneras diferentes, entonces el número de maneras distintas en que pueden suceder ambos sucesos es m x n

Ejemplo : En la etapa final de fútbol profesional de primera, cuatro equipos : CRISTAL ( C ), BOYS ( B) , ESTUDIANTES ( E ), UNIVERSITARIO (U), disputan el primer y segundo lugar (campeón y subcampeón). ¿De cuántas maneras diferentes estos equipos pueden ubicarse en dichos lugares? Solución : Utilizando el principio de multiplicación 1º 2º EXPLICACIÓN: 1 o El primer lugar puede ser ocupado por cualquiera de los cuatro equipos. 2 o El segundo lugar puede ser ocupado por cualquiera de 4 x 3 los otros tres equipos que restan 3 o Por el principio de multiplicación, se observa que el # maneras = 12 evento del primer lugar se presenta de 4 maneras y el del segundo lugar de 3 maneras distintas, entonces el número de maneras totales será : 4 x 3 = 12

Principio De Multiplicación � Si hacemos 2 experimentos, uno con n posibles resultados, y otro con m posibles resultados, el número total de resultados al realizar ambos experimentos es m x n � Ejemplos: • A partir de 10 senadores y 10 diputados se va a hacer un comité con 3 senadores y 4 diputados, de cuántas maneras diferentes se puede conformar dicho comité 12

Principio de adición ó multiplicación? � ¿Cómo podemos distinguir cuando hacer uso del principio multiplicativo y cuando del aditivo? � Cuando se trata de una sola actividad, la cual requiere para ser llevada a efecto de una serie de pasos, entonces haremos uso del principio multiplicativo y si la actividad a desarrollar o a ser efectuada tiene alternativas para ser llevada a cabo, haremos uso del principio aditivo. 13

Ejercicio: Se desea cruzar un río, para ello se dispone de 3 botes, 2 lanchas y 1 deslizador. ¿De cuantas formas se puede cruzar el río utilizando los medios de transporte señalados?

Utilizando el Principio de adición RECUERDA: Solución: Bote Lancha Deslizador 3 o 2 o 1 # maneras = 3 + 2 + 1 = 6 Si se desea que se realicen los eventos A y B , entonces se utiliza el principio de multiplicación (x) Si se desea que se realicen los eventos A ó B , entonces se utiliza el principio de adición (+)

Ejercicio: ¿Cuántas placas para automóviles pueden hacerse si cada placa consta de dos letras diferentes seguidas de tres dígitos diferentes? (considerar 26 letras del alfabeto)

Utilizando el principio de multiplicación Solución : letras Dígitos 26 x 25 x 10 x 9 x 8 # placas = 468 000 EXPLICACIÓN: 1 o. El primer casillero puede ser ocupado por cualquiera de las 26 letras 2 o. El segundo casillero puede ser ocupado por cualquiera de las 25 letras que restan 3 o. El tercer casillero puede ser ocupado por cualquiera de los 10 dígitos ( del 0 al 9) 4 o. El cuarto casillero lo pueden ocupar los 9 dígitos restantes 5 o. El quinto casiller puede ser ocupado por cualquiera de los 8 dígitos restantes 6 o. Por el principio de multiplicación, el número de placas será = 26 x 25 x 10 x 9 x 8 = 468 000

Permutaciones � Permutación: disposición lineal de objetos. � Ejemplo: en un grupo de 10 estudiantes se escogerá a 5 para tomar una foto y se les sentará en una fila. ¿Cuántas disposiciones son posibles? � ¿Cuántas disposiciones son posibles si todos los estudiantes participan en la foto?

Permutaciones �Dados n objetos, queremos obtener las diferentes formas de ordenar r de éstos objetos �Por ejemplo, dada las letras a, b, c, de cuántas formas podemos arreglar 2 de ellas: ab, ba, ac, ca, bc, cb �Esto se conoce como las permutaciones de r en n, P(n, r) 19

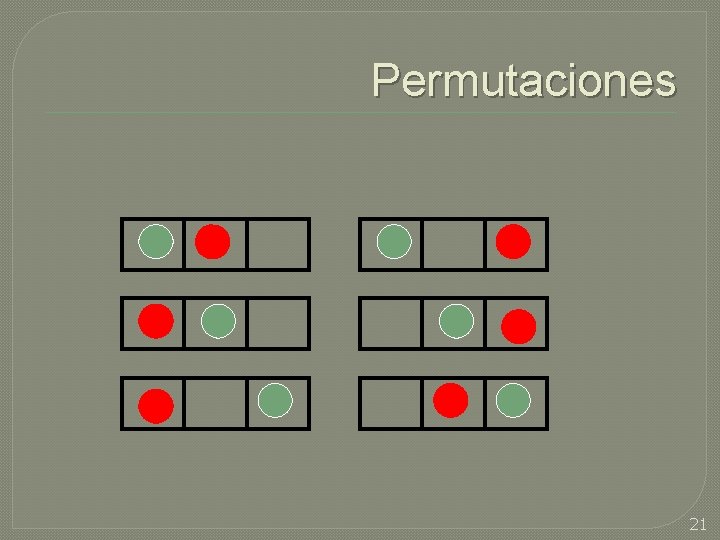
Permutaciones 20

Permutaciones 21

Permutaciones �El número de permutaciones se obtiene de la siguiente manera: P(n, r) = n! / (n-r)! �Donde n! es el factorial de n, definido como: n! = n (n-1) (n-2) …. x 2 x 1 (Por definición: 0! = 1) 22

Ejemplos: � De cuántas maneras se pueden colocar 3 pelotas diferentes (azul, verde, rojas) en 10 cajas, si en cada caja sólo cabe una pelota? � Si hay 7 oficinas, y queremos asignarle una oficina a cada uno de 4 estudiantes, de cuántas formas se pueden asignar las oficinas? � Cuántos números de 3 dígitos se pueden escribir de forma que no se repitan dígitos? 23

Permutaciones – Generalización �Ahora consideramos que tenemos t clases de objetos, de forma que los de una clase son indistinguibles entre sí �Cómo podemos ordenar n objetos, con q 1 del tipo 1, q 2 del tipo 2, …, qt del tipo t? �Por ejemplo, 3 letras, 2 a’s y 1 b: aab, aba, baa 24

Permutaciones – Generalización � Esto lo podemos calcular de la siguiente manera: n! / (q 1! q 2! … qt!) � Ejemplos: • Para el código morse (puntos y rayas), cuántos mensajes se pueden hacer con dos puntos y tres rayas? • Hay 10 oficinas, 2 las va a explorar el robot 1, 5 el robot 2, y 3 el robot 3, de cuántas formas diferentes se pueden organizar los robots para explorar las oficinas? 25

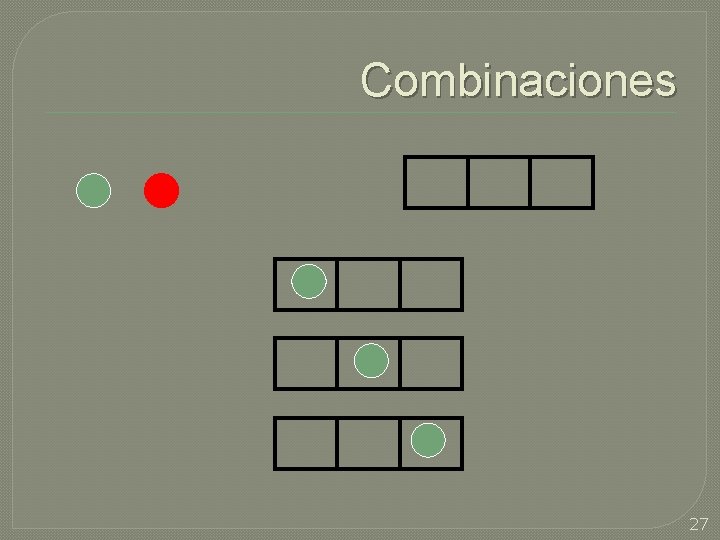
Combinaciones �Dado que tenemos n objetos, de cuántas formas podemos seleccionar r de éstos (sin importar el orden)? �Por ejemplo, tenemos 3 pelotas, una roja, una verde y otra azul, de cuántas formas se pueden sacar 2 pelotas: • (roja, verde), (roja, azul), (verde azul) 26

Combinaciones 27

Combinaciones 28

Combinaciones � Esto son las combinaciones r de n, o C(n, obtienen con la siguiente expresión: C(n, r) = n! / r! (n-r)! r), y se � Ejemplos: • De cuántas formas se pueden colocar 3 pelotas (iguales) en 10 cajas, cada caja puede tener máximo una pelota? • Cuántos números binarios de 5 dígitos con 3 unos se pueden tener? • Cuántos comités distintos de 3 personas podría haber en este grupo de 60 estudiantes? 29

Teorema del Binomio �Binomio al cuadrado: (a + b)2 = (a + b) = a 2 + ab + ba + b 2 = a 2 + 2 ab + b 2 �Binomio al cubo: (a + b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3 �En general: (a + b)n = ? 30

Teorema de Binomio �En general, cada término surge de elegir a en n-k factores y b en k factores �Por ejemplo, para el binomio al cubo: aba, aab, baa 3 a 2 b C(3, 1) a 2 b = 3 a 2 b �En general, cada término tiene como coeficiente C(n, k) 31

Teorema de Binomio �Así, un binomio a la n se puede escribir como: (a + b)n = C(n, 0) anb 0 + C(n, 1) an-1 b 1 + … + C(n, n) a 0 bn �Teorema del binomio: (a + b)n = Sk C(n, k) an-kbk 32

Triángulo de Pascal �Una forma de obtener los coeficientes es mediante el triángulo de Pascal �El triángulo tiene 1’s en las orillas, y todos los números interiores son la suma de los dos números de arriba 33

Triángulo de Pascal 1 1 1 2 3 4 1 3 6 1 4 1 34

Ejercicios � Cuántos comités diferentes de 3 personas puede haber a partir de un grupo de 10 individuos? � De cuántas diferentes maneras pueden repartirse 5 cartas a partir de 52 cartas (poker)? 35

Ejercicios � Cuántos comités de 3 estudiantes se pueden generar en el grupo (40 h, 20 m) si en el comité debe haber al menos un hombre y una mujer? � Dados 10 problemas, cuántos exámenes diferentes se pueden generar: (a) no importa el orden de los problemas, (b) si importa el orden 36

Ejercicios � Un paciente tiene 0, una o dos de 5 posibles enfermedades; y al menos un síntoma de 10 posibles síntomas. ¿Cuántas posibles combinaciones de enfermedades-síntomas puede tener? � Un robot puede observar de 1 a 3 marcas en un mapa con 50 marcas en cierto momento, cuántas posibles combinaciones de marcas puede observar 37

Ejercicios �Da los coeficientes de expandir el binomio (a+b)5 38

Generación de permutaciones � Cómo generar todas las posibles permutaciones de n objetos? � Si son pocos, lo podemos hacer “a mano”: • • • abc acb bac bca cab cba 41

Generación de permutaciones �Si son muchos, ya no es tan fácil! �Para ello requerimos de un algoritmo para generar las permutaciones �El algoritmo se basa en asignarle un número consecutivo a cada objeto (1, 2, …), de forma que las permutaciones sigan un orden, llamado orden lexicográfico 42

Orden lexicográfico � En el ejemplo, si hacemos a=1, b=2, c=3, entonces: • • • abc acb bac bca cab cba 123 132 213 231 312 321 � Están ordenadas lexicográficamente 43

Algoritmo � Iniciar con la secuencia “menor” de acuerdo al orden (1, 2, …, n) � Dada la secuencia a [a 1, a 2, …am, …an], generar la siguiente secuencia b [b 1, b 2, …bm, …bn] tal que: • De izquierda a derecha, ai=bi, hasta el máximo posible valor m • Sustituir el valor bm, por el valor más pequeño aj, j>m, que sea mayor a bm • Ordenar los demás elementos de acuerdo al orden lexicográfico � Repetir 2 hasta alcanzar la secuencia “mayor” (n, n-1, …, 1) 44

Ejemplo � Dado el elemento: • 124653 � El valor m=3 • 124… � Por lo que el elemento 4 se sustituye por el 5 (el menor de 635 que es mayor a 4): • 125… � Agregando el resto de los elementos: • 125346 45