Column Cholesky Factorization ARTR for j 1 n







- Slides: 16

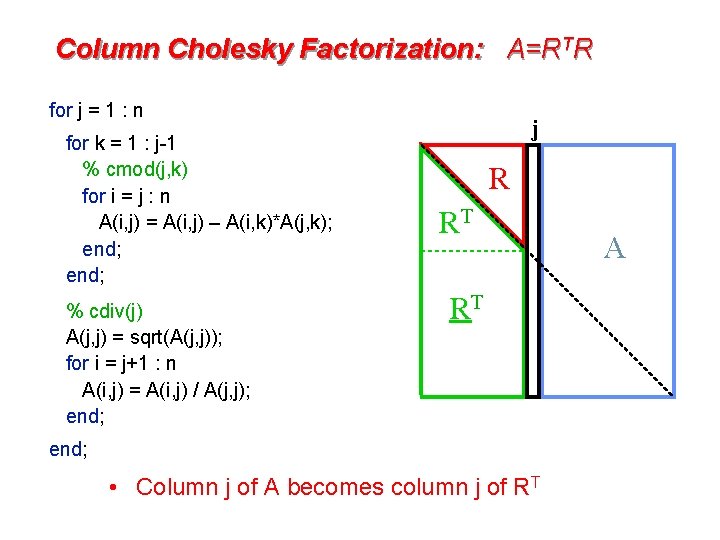
Column Cholesky Factorization: A=RTR for j = 1 : n for k = 1 : j-1 % cmod(j, k) for i = j : n A(i, j) = A(i, j) – A(i, k)*A(j, k); end; % cdiv(j) A(j, j) = sqrt(A(j, j)); for i = j+1 : n A(i, j) = A(i, j) / A(j, j); end; j R RT RT end; • Column j of A becomes column j of RT A

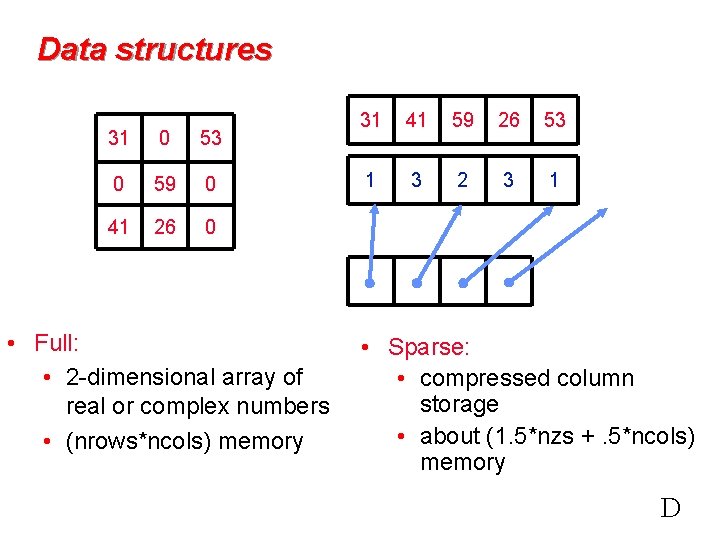
Data structures 31 0 53 0 59 0 41 26 0 • Full: • 2 -dimensional array of real or complex numbers • (nrows*ncols) memory 31 41 59 26 53 1 3 2 3 1 • Sparse: • compressed column storage • about (1. 5*nzs +. 5*ncols) memory D

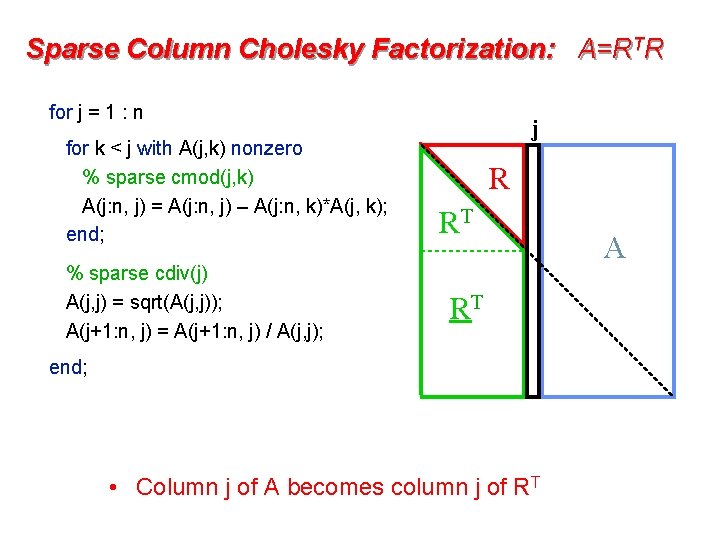
Sparse Column Cholesky Factorization: A=RTR for j = 1 : n for k < j with A(j, k) nonzero % sparse cmod(j, k) A(j: n, j) = A(j: n, j) – A(j: n, k)*A(j, k); end; % sparse cdiv(j) A(j, j) = sqrt(A(j, j)); A(j+1: n, j) = A(j+1: n, j) / A(j, j); j R RT RT end; • Column j of A becomes column j of RT A

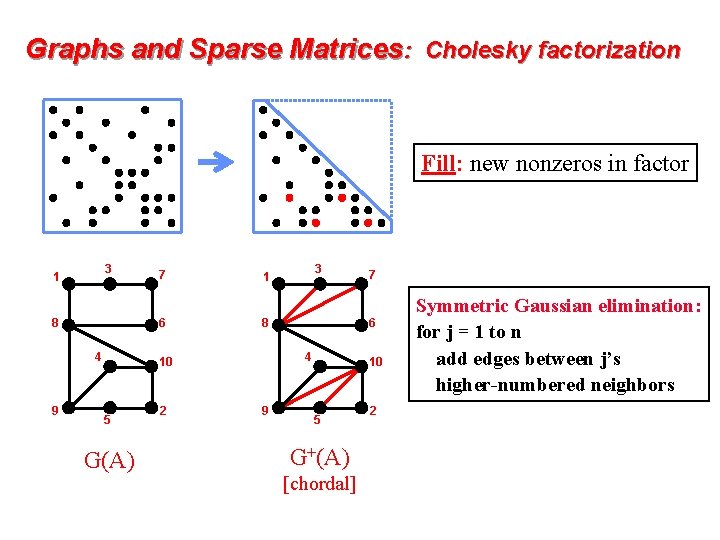
Graphs and Sparse Matrices: Cholesky factorization Fill: new nonzeros in factor 3 1 6 8 4 9 7 G(A) 2 4 9 7 6 8 10 5 3 1 10 5 G+(A) [chordal] 2 Symmetric Gaussian elimination: for j = 1 to n add edges between j’s higher-numbered neighbors

Sparse Cholesky factorization: A=RTR 1. Preorder • Independent of numerics 2. Symbolic Factorization • • Elimination tree Nonzero counts Supernodes Nonzero structure of R 3. Numeric Factorization • • Static data structure Supernodes use BLAS 3 to reduce memory traffic 4. Triangular Solves

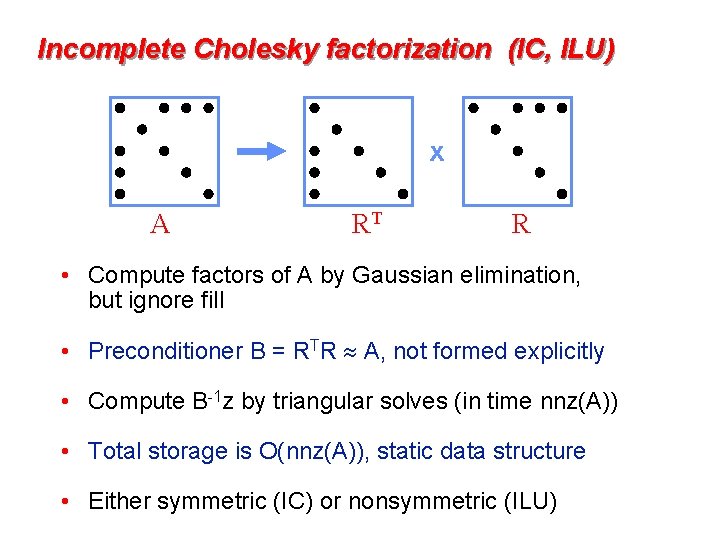
Incomplete Cholesky factorization (IC, ILU) x A RT R • Compute factors of A by Gaussian elimination, but ignore fill • Preconditioner B = RTR A, not formed explicitly • Compute B-1 z by triangular solves (in time nnz(A)) • Total storage is O(nnz(A)), static data structure • Either symmetric (IC) or nonsymmetric (ILU)

Incomplete Cholesky and ILU: Variants • Allow one or more “levels of fill” • unpredictable storage requirements 1 4 2 3 • Allow fill whose magnitude exceeds a “drop tolerance” • may get better approximate factors than levels of fill • unpredictable storage requirements • choice of tolerance is ad hoc • Partial pivoting (for nonsymmetric A) • “Modified ILU” (MIC): Add dropped fill to diagonal of U or R • A and RTR have same row sums • good in some PDE contexts

Incomplete Cholesky and ILU: Issues • Choice of parameters • good: smooth transition from iterative to direct methods • bad: very ad hoc, problem-dependent • tradeoff: time per iteration (more fill => more time) vs # of iterations (more fill => fewer iters) • Effectiveness • condition number usually improves (only) by constant factor (except MIC for some problems from PDEs) • still, often good when tuned for a particular class of problems • Parallelism • Triangular solves are not very parallel • Reordering for parallel triangular solve by graph coloring

Matrix permutations: Symmetric direct methods • Goal is to reduce fill, making Cholesky factorization cheaper. • Minimum degree: • Eliminate row/col with fewest nzs, add fill, repeat • Theory: can be suboptimal even on 2 D model problem • Practice: often wins for medium-sized problems • Nested dissection: • Find a separator, number it last, proceed recursively • Theory: approx optimal separators => approx optimal fill and flop count • Practice: often wins for very large problems • Banded orderings (Reverse Cuthill-Mc. Kee, Sloan, . . . ): • Try to keep all nonzeros close to the diagonal • Theory, practice: often wins for “long, thin” problems • Best orderings for direct methods are ND/MD hybrids.

Fill-reducing permutations in Matlab • Nonsymmetric approximate minimum degree: • p = colamd(A); • column permutation: lu(A(: , p)) often sparser than lu(A) • also for QR factorization • Symmetric approximate minimum degree: • p = symamd(A); • symmetric permutation: chol(A(p, p)) often sparser than chol(A) • Reverse Cuthill-Mc. Kee • p = symrcm(A); • A(p, p) often has smaller bandwidth than A • similar to Sparspak RCM D

Matrix permutations for iterative methods • Symmetric matrix permutations don’t change the convergence of unpreconditioned CG • Symmetric matrix permutations affect the quality of an incomplete factorization – poorly understood, controversial • Often banded (RCM) is best for IC(0) / ILU(0) • Often min degree & nested dissection are bad for no-fill incomplete factorization but good if some fill is allowed • Some experiments with orderings that use matrix values • e. g. “minimum discarded fill” order • sometimes effective but expensive to compute

Nonsymmetric matrix permutations for iterative methods • Dynamic permutation: ILU with row or column pivoting • E. g. ILUTP (Saad), Matlab “luinc” • More robust but more expensive than ILUT • Static permutation: Try to increase diagonal dominance • E. g. bipartite weighted matching (Duff & Koster) • Often effective; no theory for quality of preconditioner • Field is not well understood, to say the least

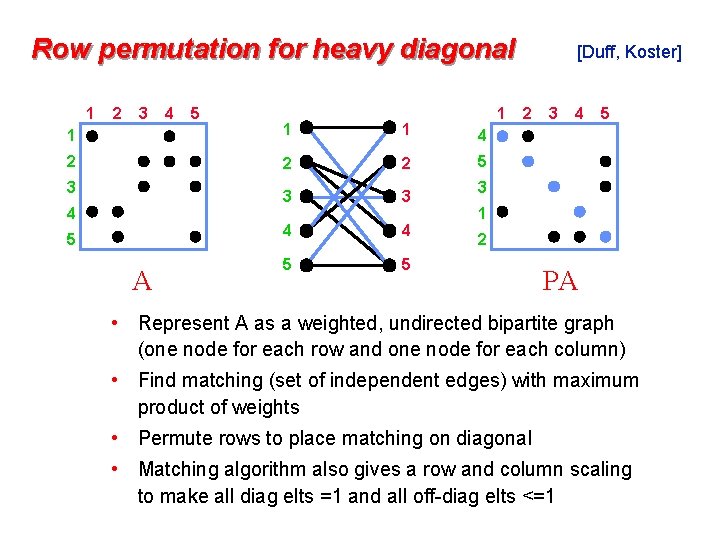
Row permutation for heavy diagonal 1 2 3 4 5 1 1 4 2 2 2 5 3 3 4 4 5 5 3 4 5 A [Duff, Koster] 2 3 4 5 3 1 2 PA • Represent A as a weighted, undirected bipartite graph (one node for each row and one node for each column) • Find matching (set of independent edges) with maximum product of weights • Permute rows to place matching on diagonal • Matching algorithm also gives a row and column scaling to make all diag elts =1 and all off-diag elts <=1

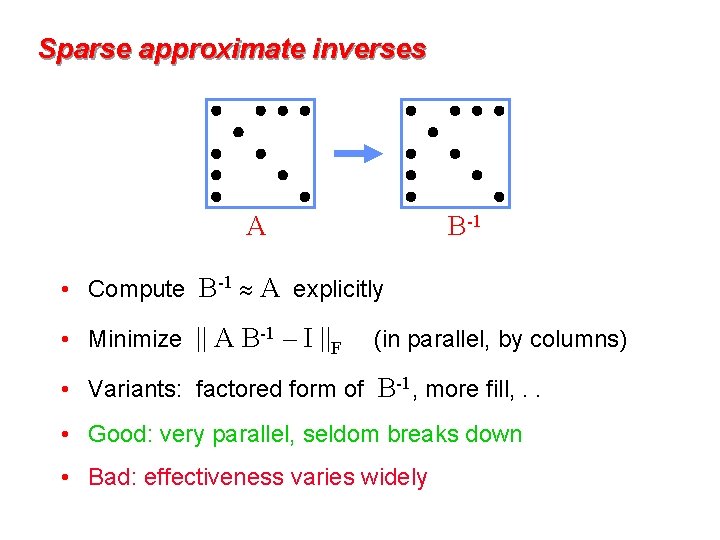
Sparse approximate inverses A B-1 • Compute B-1 A explicitly • Minimize || A B-1 – I ||F (in parallel, by columns) • Variants: factored form of B-1, more fill, . . • Good: very parallel, seldom breaks down • Bad: effectiveness varies widely

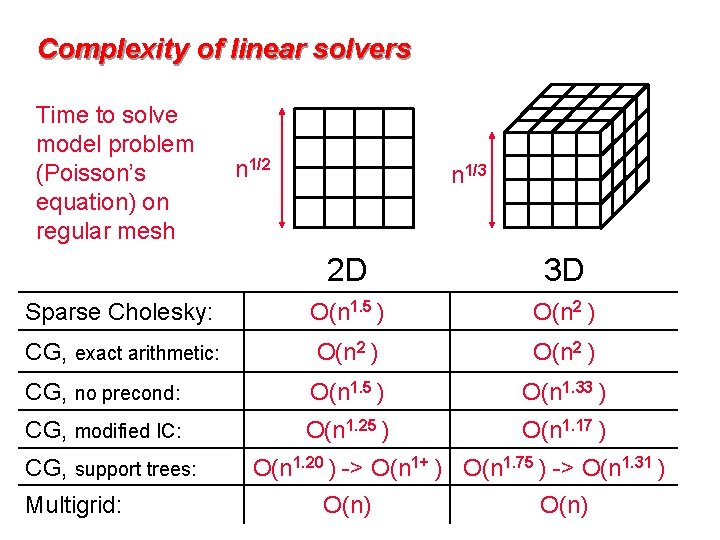
Complexity of linear solvers Time to solve model problem (Poisson’s equation) on regular mesh n 1/2 n 1/3 2 D 3 D Sparse Cholesky: O(n 1. 5 ) O(n 2 ) CG, exact arithmetic: O(n 2 ) CG, no precond: O(n 1. 5 ) O(n 1. 33 ) CG, modified IC: O(n 1. 25 ) O(n 1. 17 ) CG, support trees: Multigrid: O(n 1. 20 ) -> O(n 1+ ) O(n 1. 75 ) -> O(n 1. 31 ) O(n)

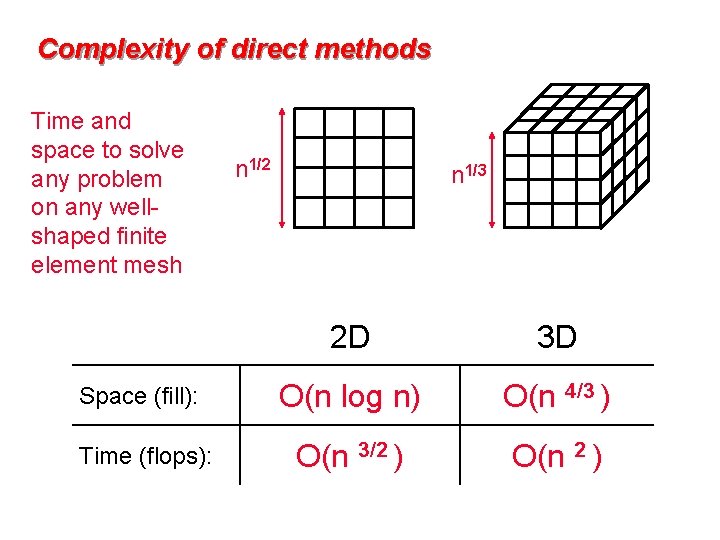
Complexity of direct methods Time and space to solve any problem on any wellshaped finite element mesh n 1/2 n 1/3 2 D 3 D Space (fill): O(n log n) O(n 4/3 ) Time (flops): O(n 3/2 ) O(n 2 )