Clouds are not spheres mountains are not cones

“Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. ” Benoit Mandelbrot Fraktálok és káosz 1. Fraktális dimenzió Szirmay-Kalos László

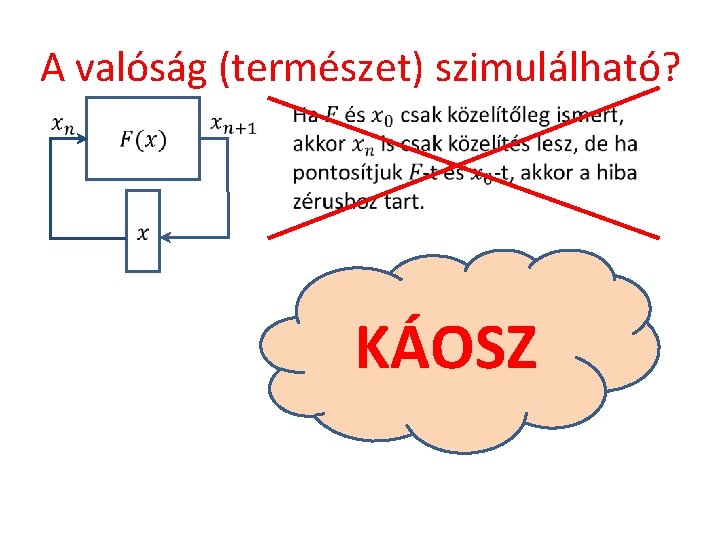
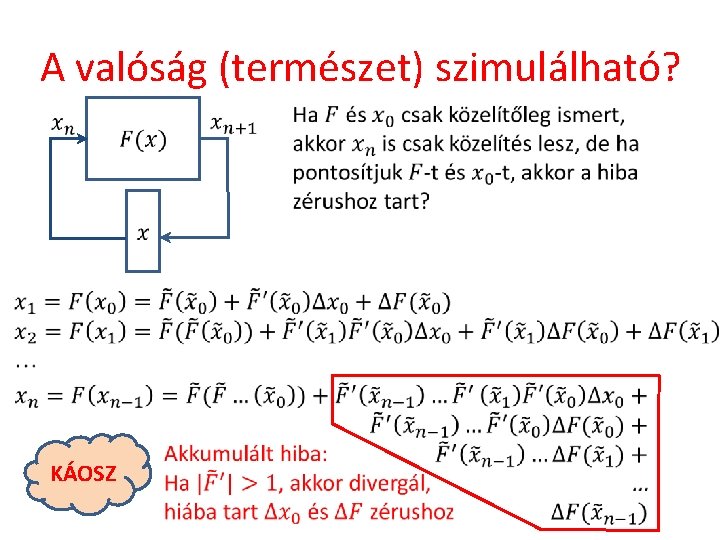
A valóság (természet) szimulálható? Hiba egy lépésben KÁOSZ

A valóság (természet) metrikus? •

(Helge von) Koch görbe: hossz végtelen • Véges tartományban végtelen hosszú: – Dimenzió > 1 • Területe zérus – Dimenzió < 2 • Folytonos • Sehol sem differenciálható (tüskés) • Önhasonló

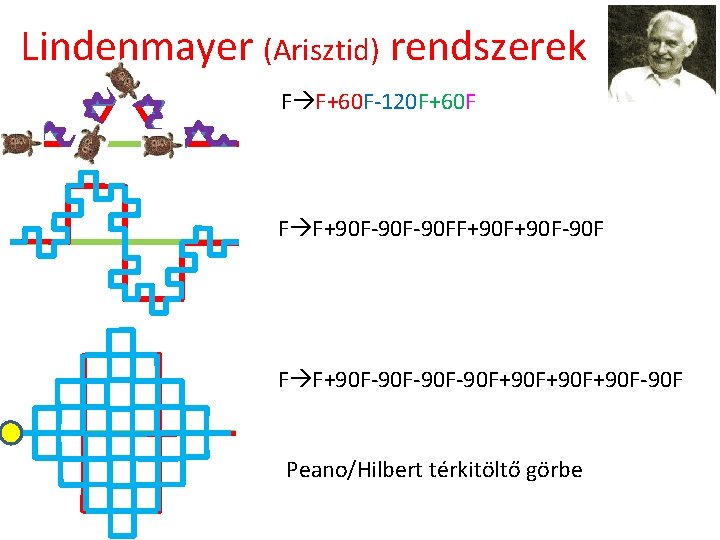
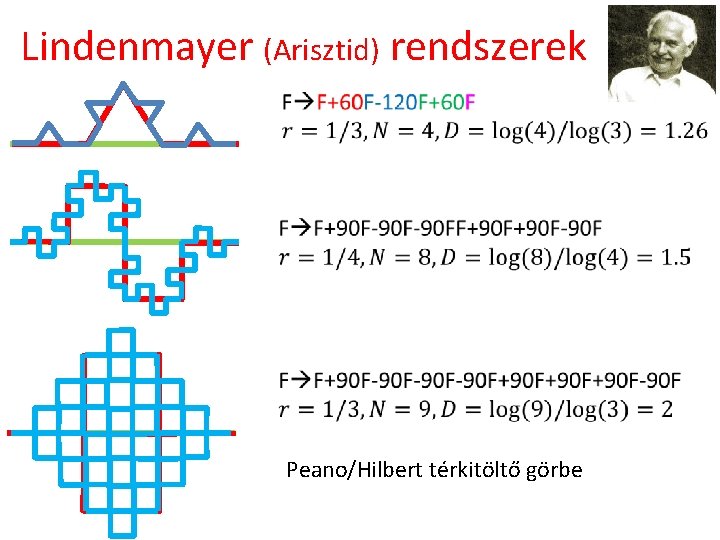
Lindenmayer (Arisztid) rendszerek F F+60 F-120 F+60 F F F+90 F-90 FF+90 F-90 F F F+90 F-90 F-90 F+90 F+90 F-90 F Peano/Hilbert térkitöltő görbe

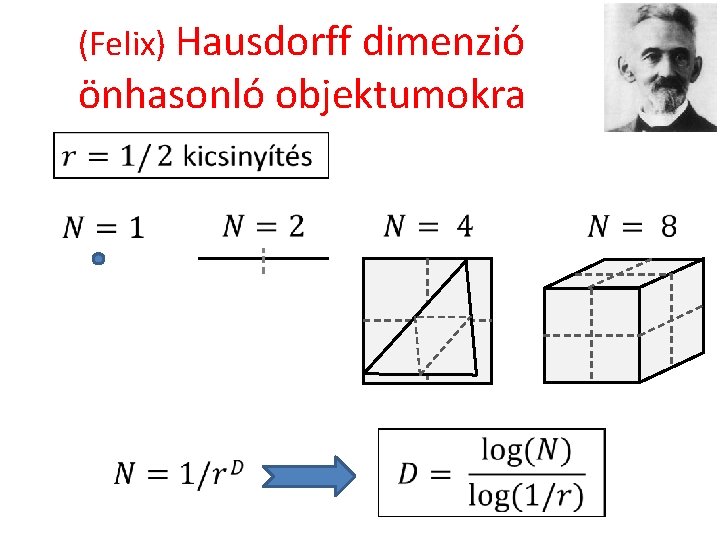
(Felix) Hausdorff dimenzió önhasonló objektumokra

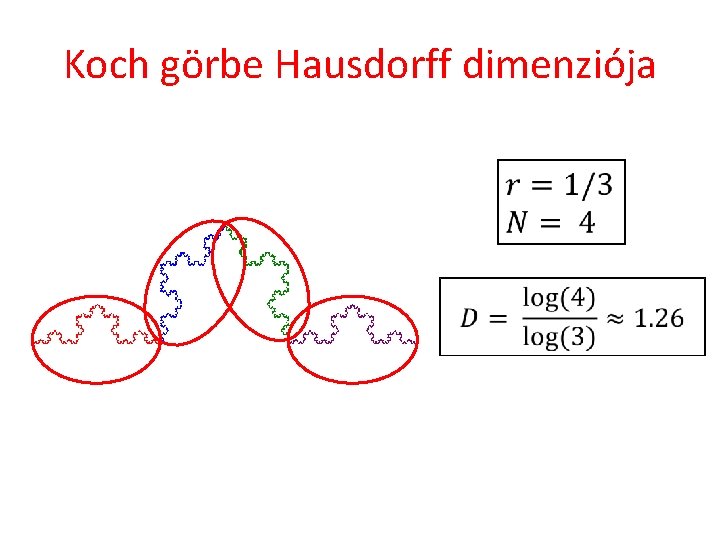
Koch görbe Hausdorff dimenziója

Lindenmayer (Arisztid) rendszerek Peano/Hilbert térkitöltő görbe

Nem önhasonló objektumok: vonalzó dimenzió

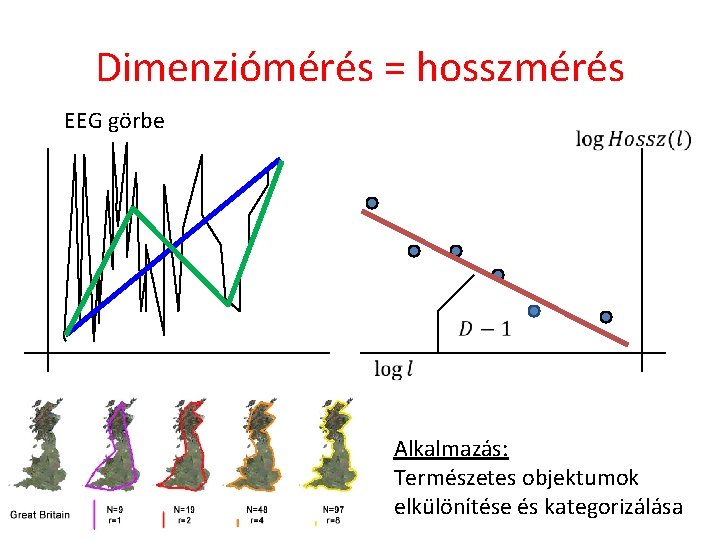
Dimenziómérés = hosszmérés EEG görbe Alkalmazás: Természetes objektumok elkülönítése és kategorizálása

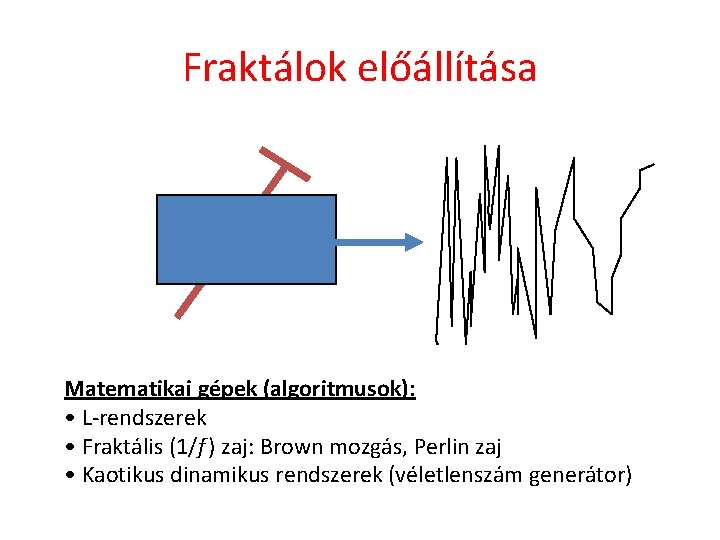
Fraktálok előállítása Matematikai gépek (algoritmusok): • L-rendszerek • Fraktális (1/f ) zaj: Brown mozgás, Perlin zaj • Kaotikus dinamikus rendszerek (véletlenszám generátor)

Lindenmayer rendszerek F F+60 F-120 F+60 F

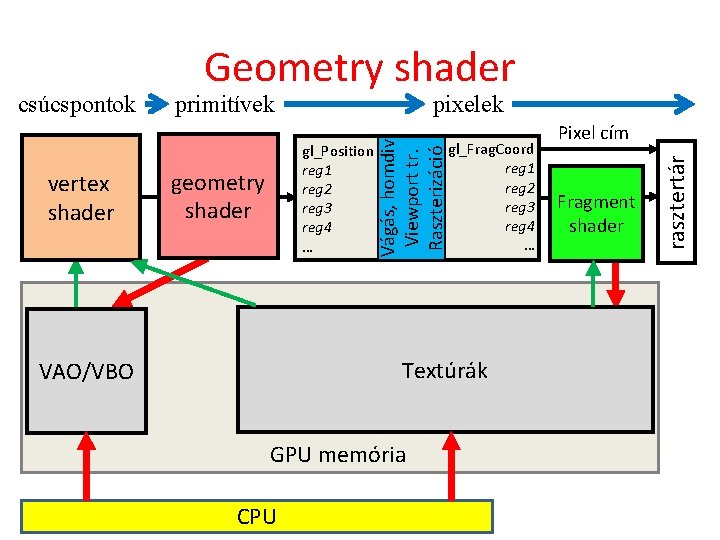
pixelek geometry shader Textúrák VAO/VBO GPU memória CPU Pixel cím Pixel szín Fragment shader rasztertár gl_Frag. Coord reg 1 reg 2 reg 3 reg 4 … gl_Position reg 1 reg 2 reg 3 reg 4 … Raszterizáció vertex shader primitívek Vágás, Homogén osztás Vágás, homdiv Viewport transzform Raszterizáció transzform csúcspontok Geometry shader

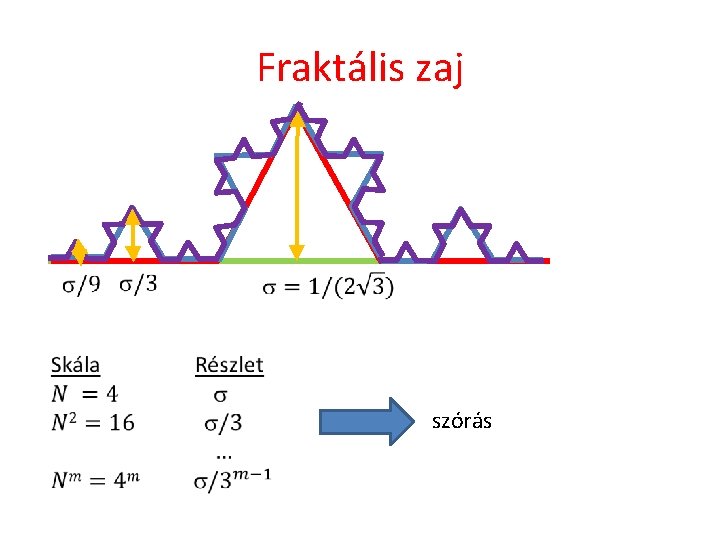
Fraktális zaj szórás

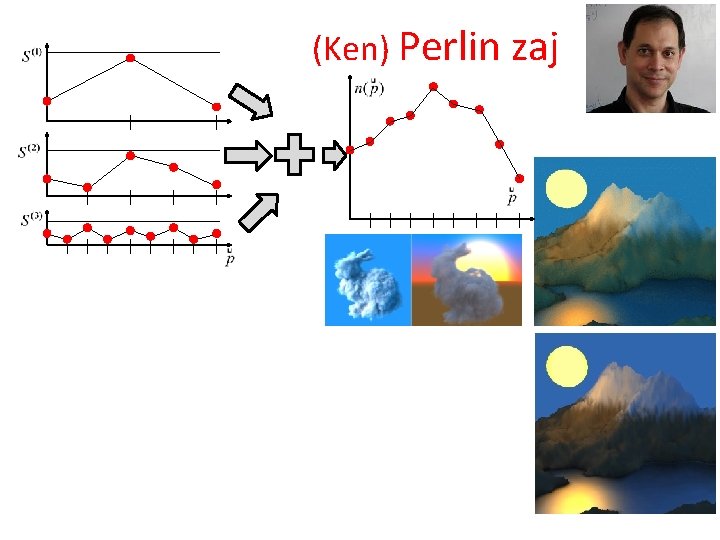
(Ken) Perlin zaj

“Invention, it must be humbly admitted, does not consist in creating out of void but of chaos. ” Mary Shelly Fraktálok és káosz 2. Káosz Szirmay-Kalos László

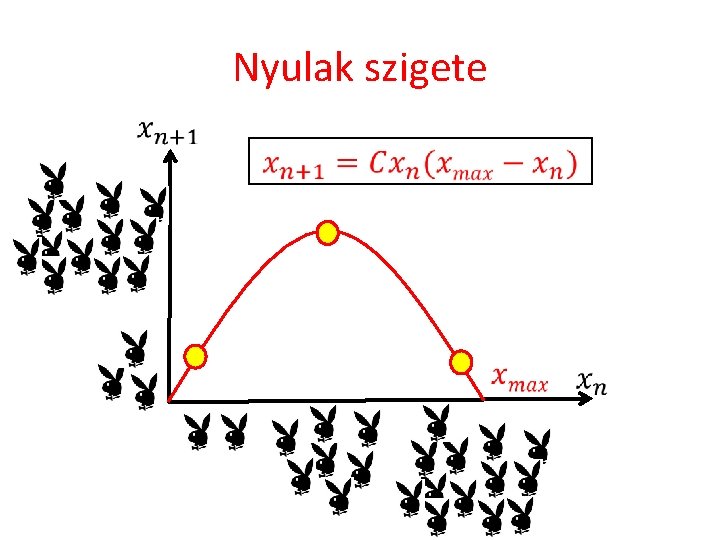
Nyulak szigete

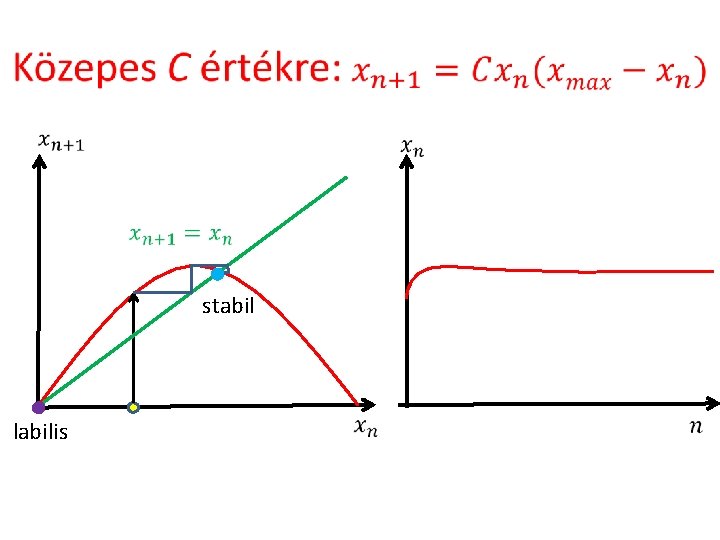
stabil labilis

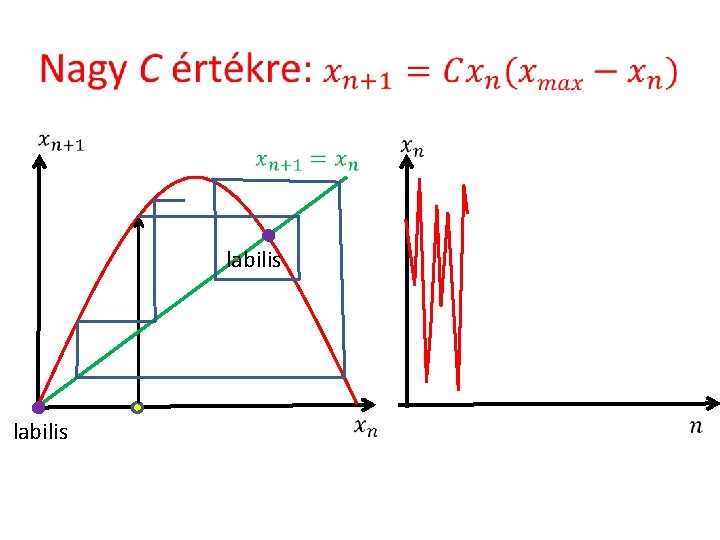
labilis

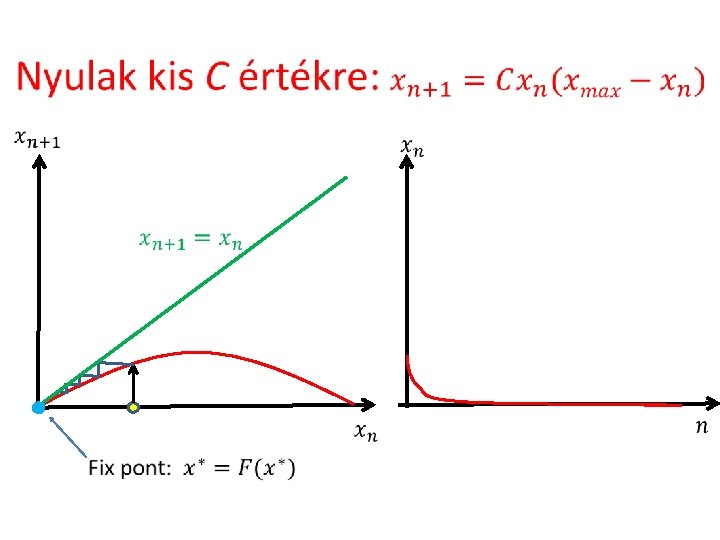
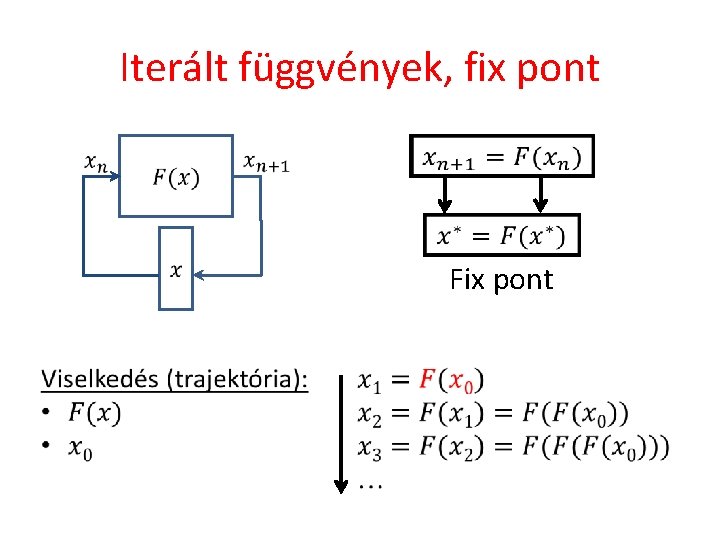
Iterált függvények, fix pont Fix pont

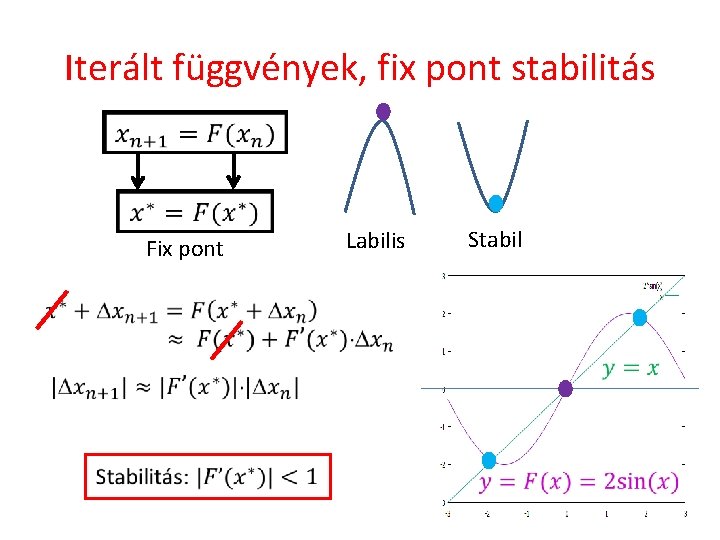
Iterált függvények, fix pont stabilitás Fix pont Labilis Stabil

A valóság (természet) szimulálható? KÁOSZ Hiba egy lépésben

A rendszer determinisztikus, de – Kezdeti állapot hatása eltűnik Edward Lorenz Káosz • Kis perturbáció nagyon eltérő viselkedéshez vezet – Auto-korrelációs függvény zérushoz tart • Korábbi állapot gyengén befolyásolja a sokkal későbbit • Megjósolhatatlanság – Teljesítmény sűrűség spektrum nem tart zérushoz • Nagy frekvencia

Pszeudó véletlenszám generátor static uint x = 3; void seed(uint s) { x = s; } uint rand( ) { x = F(x); return x; }

“There's no sense in being precise when you don't even know what you're talking about. ” Neumann János Fraktálok és káosz 3. Kaotikus rendszerek a síkon Szirmay-Kalos László

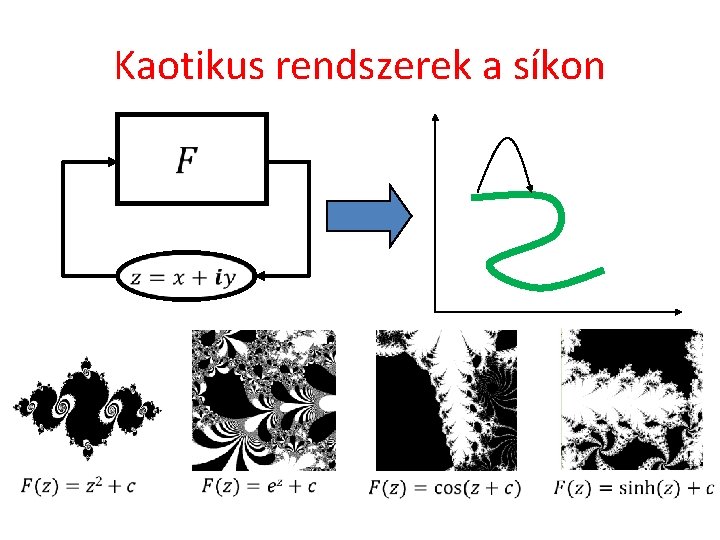
Kaotikus rendszerek a síkon

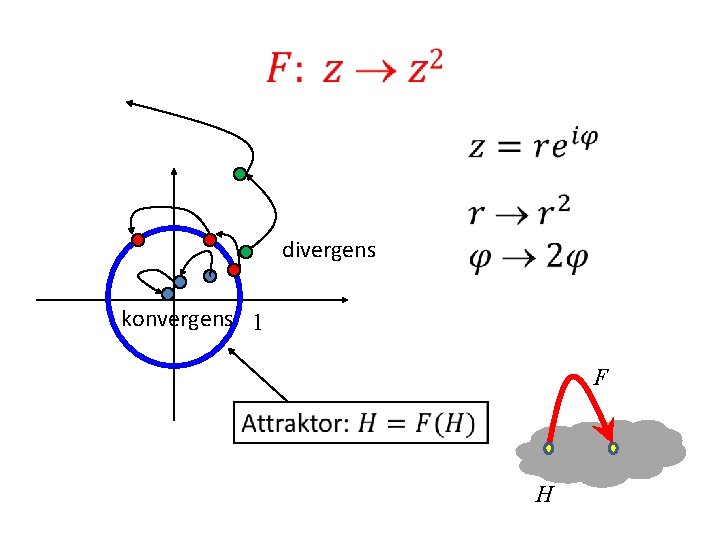
divergens konvergens 1 F H

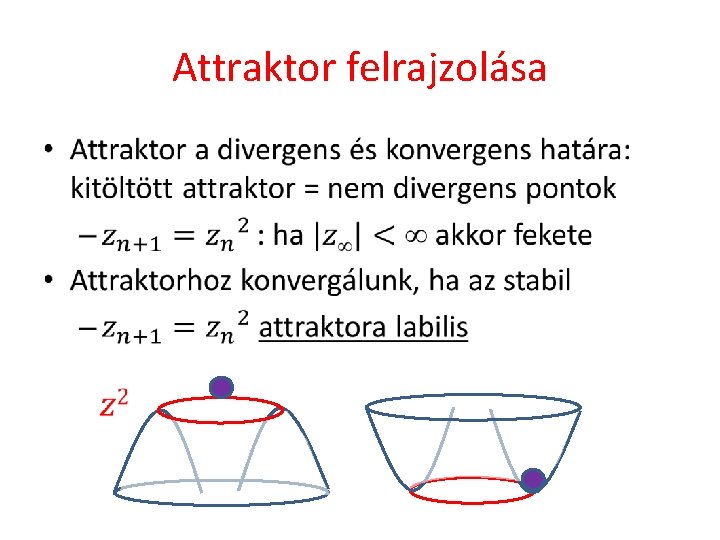
Attraktor felrajzolása •

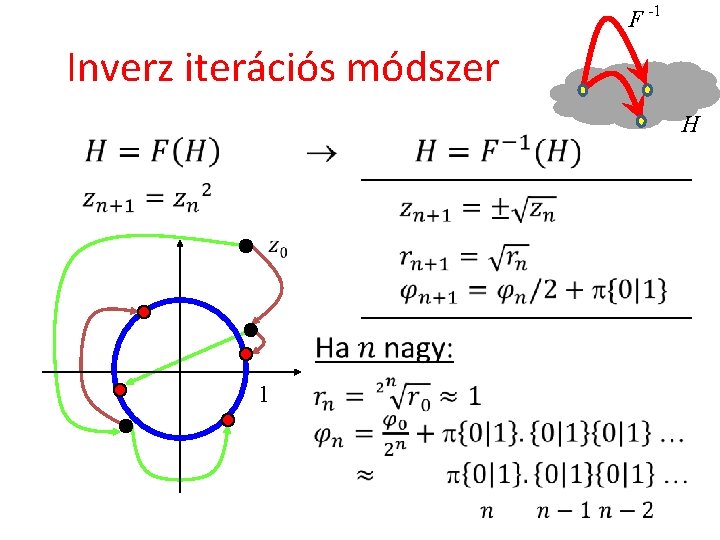
F -1 Inverz iterációs módszer H 1

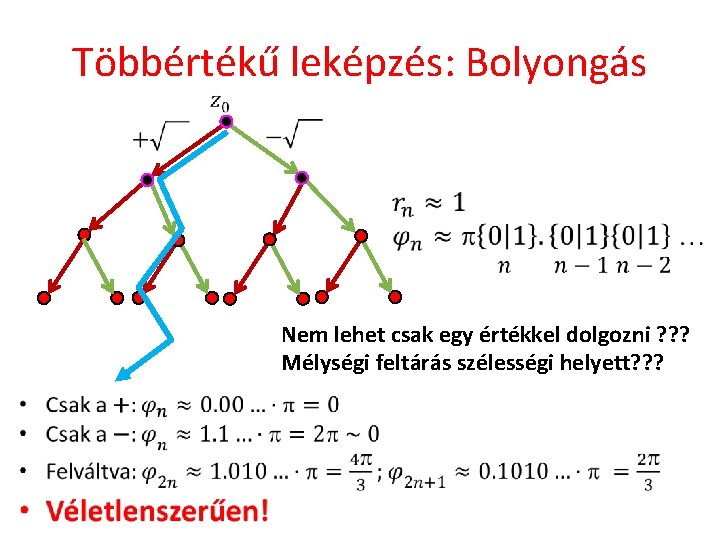
Többértékű leképzés: Bolyongás Nem lehet csak egy értékkel dolgozni ? ? ? Mélységi feltárás szélességi helyett? ? ?

Kitöltött Julia halmaz: algoritmus

GPU implementáció float c. Vtx[] = { -1, 1, 1, -1, 1 }; CPU program gl. Buffer. Data(GL_ARRAY_BUFFER, sizeof(c. Vtx), c. Vtx, GL_STATIC_DRAW); … gl. Draw. Arrays(GL_TRIANGLE_FAN, 0, 4); Vertex shader uniform vec 2 camera. Center, camera. Size; layout(location = 0) in vec 2 c. Vertex; out vec 2 z 0; void main() { gl_Position = vec 4(c. Vertex, 0, 1); z 0 = c. Vertex * camera. Size/2 + camera. Center; } uniform vec 2 c; in vec 2 z 0; out vec 4 frag. Col; Fragment shader void main() { vec 2 z = z 0; for(int i=0; i<1000; i++) z = vec 2(z. x*z. x-z. y*z. y, 2*z. x*z. y) + c; frag. Col = (dot(z, z) < 100) ? vec 4(0, 0, 0, 1) : vec 4(1, 1, 1, 1); }

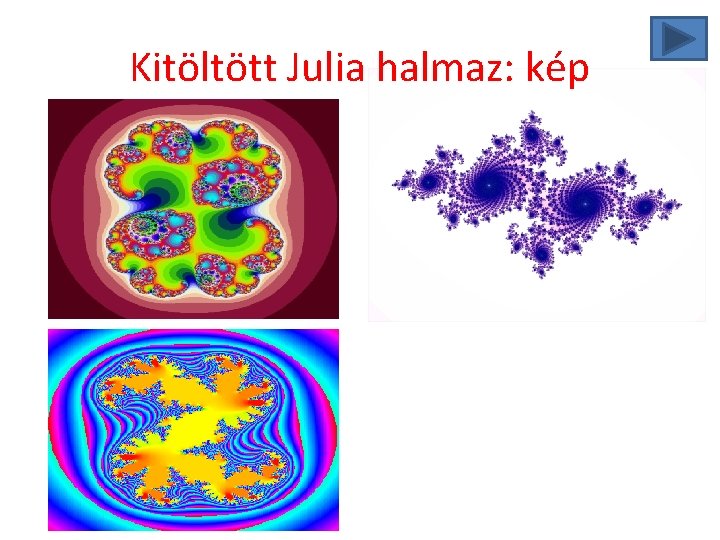
Kitöltött Julia halmaz: kép

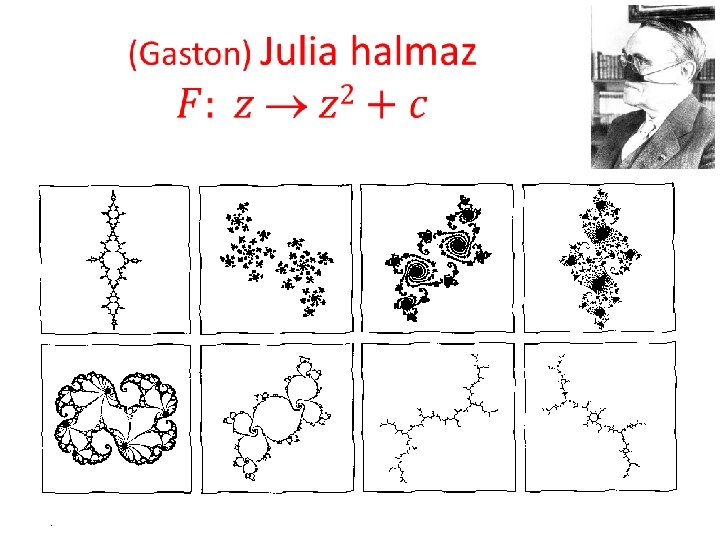
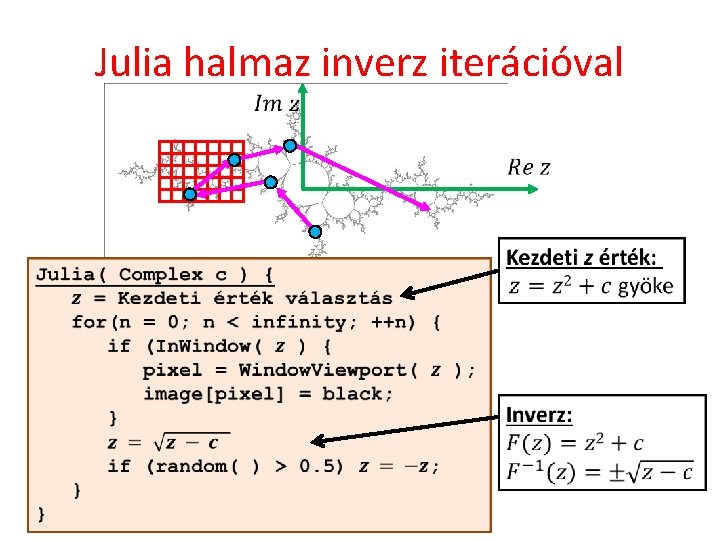
Julia halmaz inverz iterációval

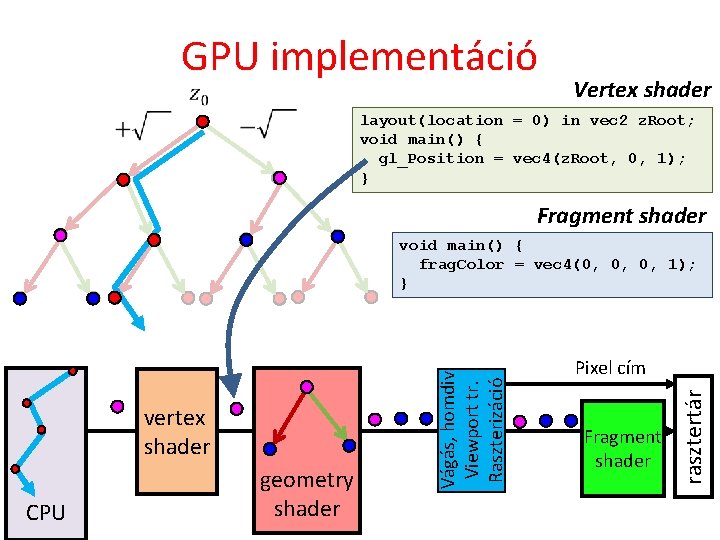
GPU implementáció Vertex shader layout(location = 0) in vec 2 z. Root; void main() { gl_Position = vec 4(z. Root, 0, 1); } Fragment shader CPU geometry shader Pixel cím Fragment shader rasztertár vertex shader Vágás, homdiv Viewport tr. Raszterizáció void main() { frag. Color = vec 4(0, 0, 0, 1); }

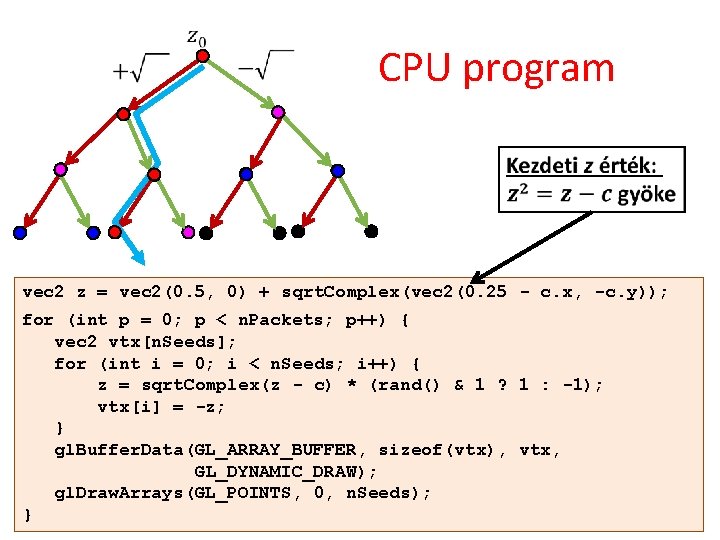
CPU program vec 2 z = vec 2(0. 5, 0) + sqrt. Complex(vec 2(0. 25 - c. x, -c. y)); for (int p = 0; p < n. Packets; p++) { vec 2 vtx[n. Seeds]; for (int i = 0; i < n. Seeds; i++) { z = sqrt. Complex(z - c) * (rand() & 1 ? 1 : -1); vtx[i] = -z; } gl. Buffer. Data(GL_ARRAY_BUFFER, sizeof(vtx), vtx, GL_DYNAMIC_DRAW); gl. Draw. Arrays(GL_POINTS, 0, n. Seeds); }

Geometry shader uniform vec 2 camera. Center, camera. Size, c; layout(points) in; layout(points, max_vertices = 63) out; vec 2 sqrt. Complex(vec 2 z) { float r = length(z), phi = atan(z. y, z. x); return vec 2(cos(phi/2), sin(phi/2)) * sqrt(r); } 0 1 2 void main() { vec 2 zs[63]; 3 4 5 zs[0] = gl_in[0]. gl_Position. xy; gl_Position = vec 4((zs[0]-camera. Center)/(camera. Size/2), 0, 1); Emit. Vertex(); for(int i = 0; i < 63/2; i++) { vec 2 z = sqrt. Complex(zs[i] - c); for(int j = 1; j <= 2; j++) { zs[2 * i + j] = z; gl_Position = vec 4((z-camera. Center)/(camera. Size/2), 0, 1); Emit. Vertex(); z = -z; } } End. Primitive(); } 6

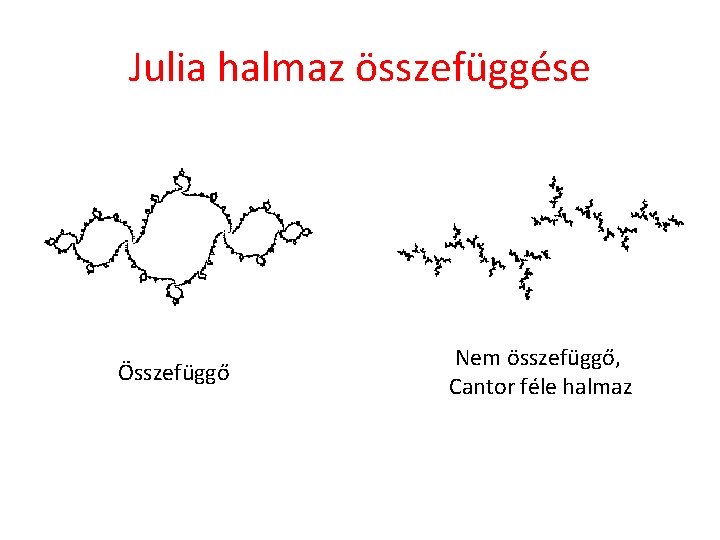
Julia halmaz összefüggése Összefüggő Nem összefüggő, Cantor féle halmaz

(Benoit) Mandelbrot halmaz

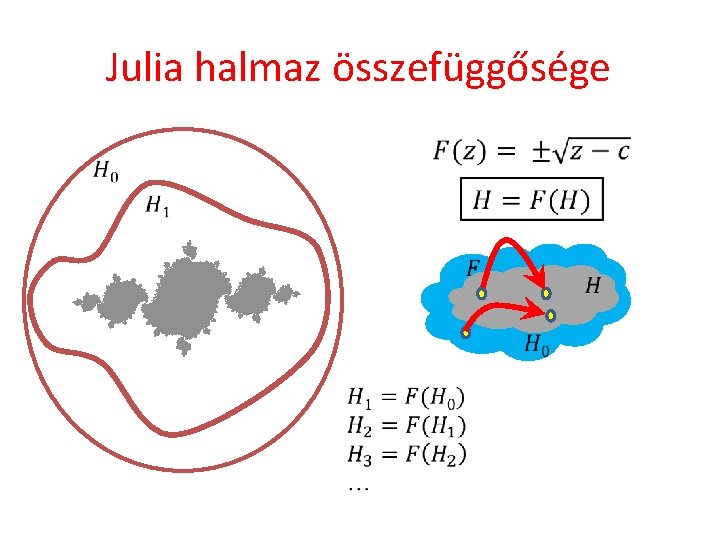
Julia halmaz összefüggősége

Julia halmaz összefüggősége

(Benoit) Mandelbrot halmaz

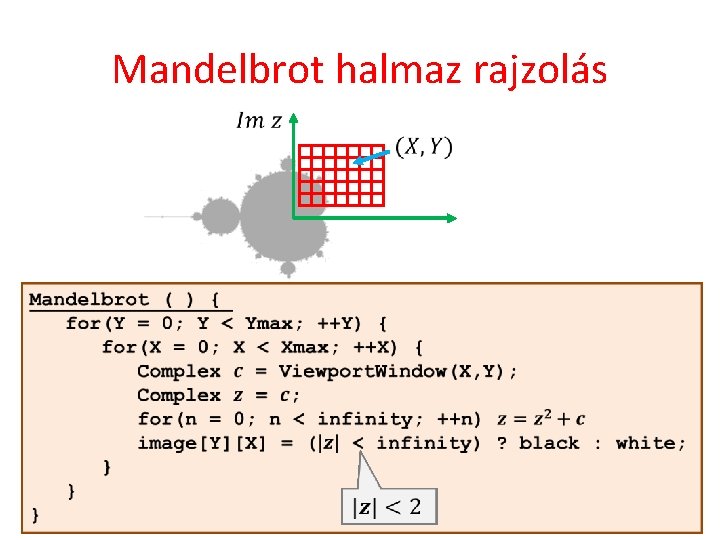
Mandelbrot halmaz rajzolás

GPU implementáció float c. Vtx[] = { -1, 1, 1, -1, 1 }; gl. Buffer. Data(GL_ARRAY_BUFFER, sizeof(c. Vtx), c. Vtx, GL_STATIC_DRAW); … CPU program gl. Draw. Arrays(GL_TRIANGLE_FAN, 0, 4); uniform vec 2 camera. Center, camera. Size; layout(location = 0) in vec 2 c. Vertex; out vec 2 c; void main() { gl_Position = vec 4(c. Vertex, 0, 1); c = c. Vertex * camera. Size/2 + camera. Center; } in vec 2 c; out vec 4 frag. Col; const int n. Iteration = 1000; Vertex shader Fragment shader void main() { vec 2 z = c; for(int i = 0; i < n. Iteration; i++) { z = vec 2(z. x * z. x - z. y * z. y, 2 * z. x * z. y) + c; if (dot(z, z) > 4) break; } frag. Col = (i == n. Iteration) ? vec 4(0, 0, 0, 1) : vec 4(1, 1, 1, 1); }

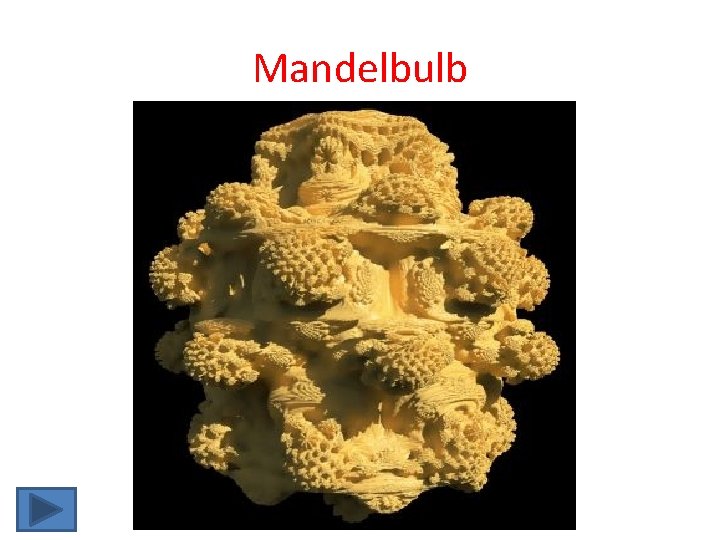
Mandelbulb

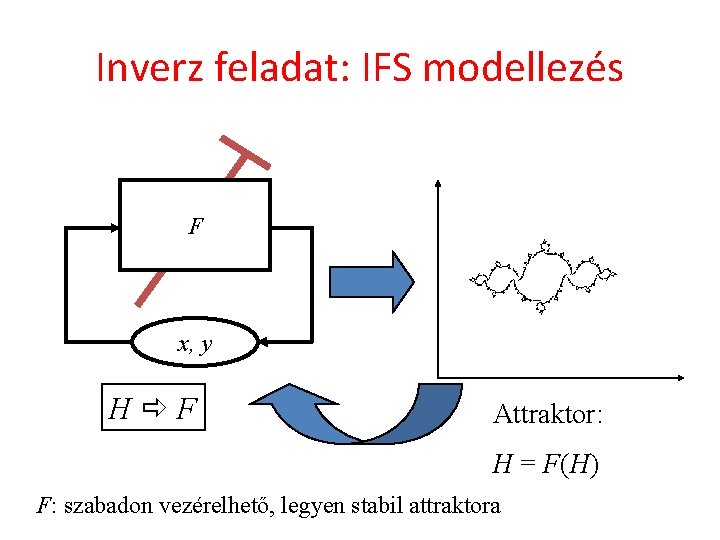
Inverz feladat: IFS modellezés F x, y H F Attraktor: H = F(H) F: szabadon vezérelhető, legyen stabil attraktora

Melyik függvény attraktora a Koch görbe? Attraktor: H = F(H) = W 1(H) W 2 (H) W 3 (H) W 4 (H) W 2 (H) W 3 (H) W 1(H) Wk (x, y) = [x, y] Ak + qk W 4 (H)

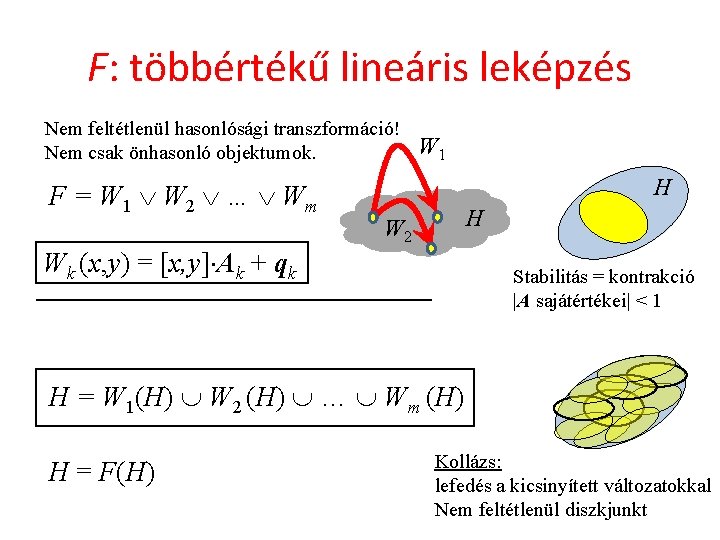
F: többértékű lineáris leképzés Nem feltétlenül hasonlósági transzformáció! Nem csak önhasonló objektumok. F = W 1 W 2 … Wm W 1 H H W 2 Wk (x, y) = [x, y] Ak + qk Stabilitás = kontrakció |A sajátértékei| < 1 H = W 1(H) W 2 (H) … Wm (H) H = F(H) Kollázs: lefedés a kicsinyített változatokkal Nem feltétlenül diszkjunkt

IFS rajzolás: iterációs algoritmus IFSDraw ( ) Legyen [x, y] = [x, y] A 1 + q 1 megoldása a kezdő [x, y] FOR i = 0 TO “infinity” DO IF In. Window(x, y) Window. Viewport(x, y X, Y) Write(X, Y, color); y ENDIF (X, Y) Válassz k-t pk valószínűséggel [x, y] = [x, y] Ak + qk x ENDFOR END Wk

Egyszerű IFS-ek

IFS modellezés

IFS képek