Unit 29 PYRAMIDS AND CONES VOLUMES SURFACE AREAS

Unit 29 PYRAMIDS AND CONES: VOLUMES, SURFACE AREAS, AND WEIGHTS 1

DEFINITIONS p p A pyramid is a polyhedron whose base can be any polygon and whose other faces are triangles that meet at a common point called the vertex Pyramids are named according to the shape of the bases, such as triangular, quadrilateral, pentagonal, hexagonal, and octagonal In a regular pyramid the base is a regular polygon, and the lateral edges are all equal in length A circular cone is a solid figure with a circular base and a surface that tapers from the base to a point called the vertex 2

DEFINITIONS p p p The axis of a circular cone is a line that connects the vertex to the center of the circular base In a right circular cone the axis is perpendicular to the base The volume of a pyramid or a right circular cone equals one third the product of the area of the base and height 3

VOLUME EXAMPLE p Find the volume of the Luxor in Las Vegas (square pyramid) shown below: • V = • AB = (646) = 417316 ft 2 350 feet • Now, 4

COMPUTING HEIGHTS AND BASES p A tent in the shape of a regular pyramid is designed to contain 6. 40 cubic meters of airspace. The base of the tent is a square with each side 2. 80 meters long. What is the height of the tent? – Compute the area of the base – The base is a square, its area is 2. 8 m = 7. 84 m 2 – Substitute the known values into the volume formula and transpose to find the height h = 2. 45 m Ans 5

LATERAL AREAS p p p Slant heights are used in determining lateral areas of pyramids and cones The slant height of a regular pyramid is the length of the altitude of any of the lateral faces The slant height of a right circular cone is the distance from the vertex to any point on the edge of the circular base The lateral area of a regular pyramid equals one half the product of the perimeter of the base and the slant height The lateral area of a right circular cone equals one half the product of the circumference of the base and the slant height 6

LATERAL AREA EXAMPLE p Determine the lateral area of the miniature scale steeple (right circular cone) shown below: (10 in tall and 6 in diam) – First the slant height must be determined using the Pythagorean Theorem – Determine the circumference of the base CB = d = (6") = 18. 85 inches – Now find the lateral area LA = ½ CB hs = ½(18. 85")(10. 44") = 98. 397 in 2 Ans 7

SURFACE AREA EXAMPLE p p The total surface area of a pyramid or cone includes the base plus the lateral area Determine the total surface area of the pyramid shown below: – First find the lateral area – Now find the total surface area SA = LA + AB = 128 in 2 + (4" 4") = 144 in 2 Ans 8

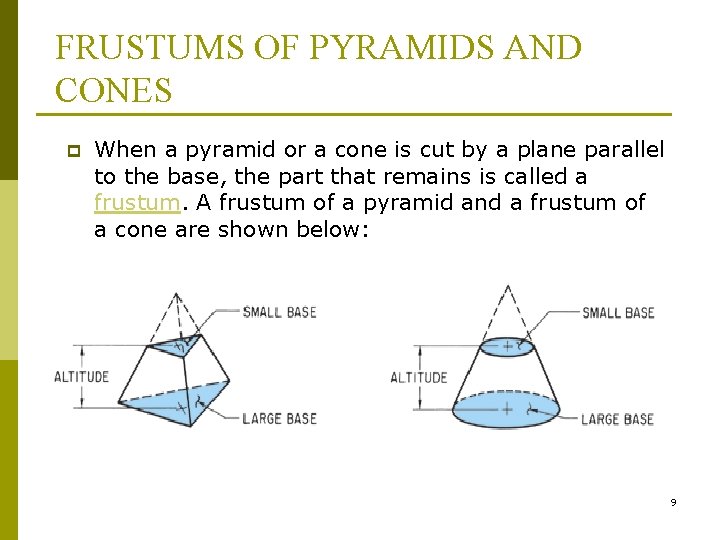
FRUSTUMS OF PYRAMIDS AND CONES p When a pyramid or a cone is cut by a plane parallel to the base, the part that remains is called a frustum. A frustum of a pyramid and a frustum of a cone are shown below: 9

VOLUMES OF FRUSTUMS p The volume of the frustum of a pyramid or cone is given as: n where V = volume p h = height p AB = area of the larger base p Ab = area of the smaller base p 10

VOLUMES OF FRUSTUMS p The formula for the volume of a frustum of a right circular cone is given as: n where V = volume p h = height p R = radius of larger base p r = radius of smaller base p 11

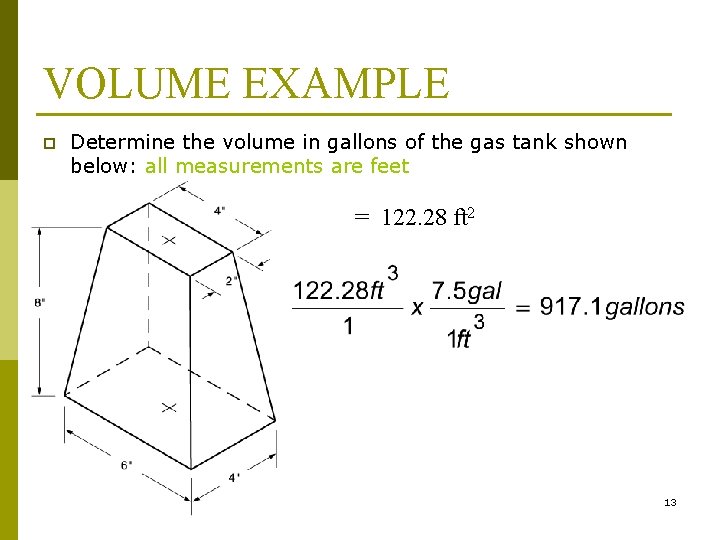
VOLUME EXAMPLE p Determine the volume in gallons of the gas tank shown below: all measurements are feet – Find AB and Ab AB = 4’ 6’ = 24 ft 2 Ab = 2’ 4’ = 8 ft 2 – Now find the volume by substituting in the known values = 122. 28 ft 2 12

VOLUME EXAMPLE p Determine the volume in gallons of the gas tank shown below: all measurements are feet = 122. 28 ft 2 13

LATERAL AREA p The lateral area of the frustum of a regular pyramid is given as: n where LA = lateral area p hs = slant height p PB = perimeter of larger base p Pb = perimeter of smaller base p 14

LATERAL AREA p The formula for the lateral area of the frustum of a right circular cone is given as: n where LA = lateral area p hs = slant height p R = radius of larger base p r = radius of smaller base p 15

SURFACE AREA p The surface area of the frustum of a pyramid or cone equals the sum of the lateral area, the larger base area, and the smaller base area n where SA = surface area p LA = lateral area p AB = area of larger base p Ab = area of smaller base p 16

SURFACE AREA EXAMPLE p Determine the surface area of the circus/elephant pedestal shown below: all measurements are feet – First find the lateral area LA = hs(R + r) = (8)(6 + 3 ) = 226. 19 ft 2 – Determine AB and Ab AB = (6)2 = 113. 10 ft 2 Ab = (3)2 = 28. 27 ft 2 – Now find the surface area: SA = LA + AB + Ab 17 = 226. 19 + 113. 10 + 28. 27 = 367. 56 ft 2 Ans

PRACTICE PROBLEMS p Round all answers in the following story problems to two decimal places whenever necessary: 1. 2. 3. 4. 5. Determine the volume of a right circular cone drinking cup with a base diameter of 6. 2 cm and a height of 13. 0 cm. Determine the lateral area of the cup in problem #1. Determine the surface area of the cup in problem #1. Find the volume of a pyramidal “rubics cube” with a height of 7 inches and a square base with 6 -inch sides. Determine the lateral area of the pyramid in problem #4. 18

PRACTICE PROBLEMS (Cont) Determine the surface area of the pyramid in problem #4. 7. Find the base diameter of a funnel (right circular cone, forget the hole) that has a volume of 840 in 3 and a height of 14. 2 inches. 8. Determine the volume of a drinking glass with a top radius of 3. 5 in and base radius of 2 in and a height of 9 in. 9. Determine the lateral area of the cone in problem #8. Make sure you use slant height and not height! 10. Determine the surface area of the cone in problem #8. 6. 19

PROBLEM ANSWER KEY 130. 83 cm 3 2. 130. 16 cm 2 3. 160. 35 cm 2 4. 84 in 3 5. 91. 39 in 2 6. 127. 39 in 2 7. 15. 03 in 8. 219. 13 in 3 9. 156. 03 in 2 10. 207. 08 in 2 1. 20